[整理]FFT(快速傅里叶变换)随记
0.前言
本文对信息学竞赛中的 FFT 算法及其推导作出一点粗浅的探讨,希望能够帮到大家一点点。
另:作者默认大家已经有了一些高中数学基础,对于课本内基础知识部分可能会涉及较少。建议初中生先学完有关三角函数、复数、向量的部分之后再来学习 FFT 。
1.前置知识
多项式
形如\(A(x)=\sum_{i=0}^n a_ix^i\)的式子称作多项式(Polynomial),多项式可以进行加减乘(除法在此不涉及)等运算。
这种表示方法称作多项式的系数表示(Coefficient representation),多项式还有一种点值表示(Point-value representation)法:
众所周知,平面上的\(n\)个点\((x_1,A(x_1))\cdots(x_n,A(x_n))\)可以唯一确定一个\(n-1\)次多项式,于是我们就用这些点来表示一个多项式。
点值表示的优点:将多项式乘法的复杂度由系数表示的\(O(n^2)\)减少到了\(O(n)\)(只需要将点值相乘)。
缺点:系数表示与点值表示的互化还是需要\(O(n^2)\),不过它是可以优化的(这也正是 FFT 做的事情)。
复数及其运算
首先我们有\(\sqrt{-1}=i\),并将形如\(z=a+bi\ (a,b\in\mathbb{R})\)的数称为复数,并定义其共轭\(\bar{z}=a-bi\)。
其中,\(\Re z=a\)称为实部,\(\Im z=b\)称为虚部。
以上是复数的代数表示,其运算同多项式运算,运算时要注意\(i^2=-1\)。(例如\((a+bi)(c+di)=(ac-bd)+(ad+bc)i\))
复数还可以与平面上的向量一一对应,我们把这种表示叫做复数的几何表示,该平面叫做复平面。
对于一个复数,它的几何表示由模长(向量的长度)和幅角(从\(x\)轴正半轴逆时针转到该向量的角度)组成。
复数几何表示的加减法运算同向量运算,而乘法的规则是模长相乘、幅角相加。
欧拉公式:\(e^{i\theta}=\cos\theta+i\sin\theta\)。
单位根及其性质
接下来车速加快,请仔细阅读!
定义方程\(z^n=1\)的复数根为\(n\)次单位根,记作\(\omega_n^k=e^{\frac{2\pi ki}{n}}\ (k=0,1,\cdots,n-1)\)。容易发现,这\(n\)个单位根恰好将单位圆\(n\)等分。
如图,这是方程\(z^3=1\)的三个复数根\(1,-\dfrac 12+\dfrac{\sqrt{3}}2i,-\dfrac 12-\dfrac{\sqrt{3}}2i\):
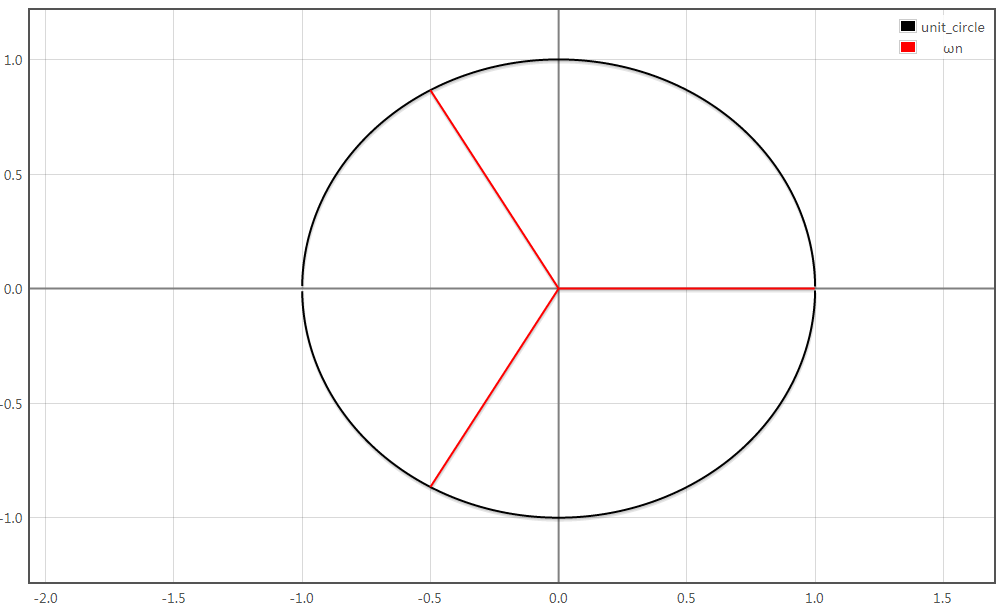
如果一个单位根的\(0,\cdots,n-1\)次方恰好构成互不相同的所有单位根,我们就将其称为本原单位根。
显然\(\omega_n=e^{\frac{2\pi i}{n}}\)是一个\(n\)次本原单位根(为方便,下文中“本原单位根”即特指\(\omega_n\))。
单位根有一些美妙的性质,我们来看一下。(假设以下的\(n\)都是正偶数)
\(\text{Theorem 1: }\omega_n^{2k}=\omega_{\frac{n}2}^k\)
\(\text{Proof: }\)利用复数几何表示的相乘法则证明。
\(\text{Theorem 2: }\omega_n^{\frac{n}2+k}=-\omega_n^k\)
\(\text{Proof: }\)可以理解为多转了半圈之后恰与原来相反。
习题一:写出方程\(z^6=1\)的所有复数根。
2.Cooley-Tukey算法
该算法分为两个过程: DFT(Discrete Fourier Transform) 和 IDFT(Inverse Discrete Fourier Transform) ,主要思想是分治。
铺垫了这么多,我们要想,如何利用单位根的一些性质来减少运算量呢?
两位巨佬 Cooley 和 Tukey 想出了一种方法:将每一项按照指数奇偶分类。
我们要计算一个多项式的 DFT ,也就是计算其点值表示,需要将每一个单位根代入计算。
即\(A(\omega_n^k)=\sum_{j=0}^{n-1}a_i\omega_n^{kj}=\sum_{j=0}^{\frac{n}2-1}a_{2j}\omega_n^{2kj}+\omega_n^k\sum_{j=0}^{\frac{n}2-1}a_{2j+1}\omega_n^{2kj}\)。
根据刚刚提到的\(\text{Theorem 1}\),我们可以将其改写成\(\sum_{j=0}^{\frac{n}2-1}a_{2j}\omega_{\frac{n}2}^{kj}+\omega_n^k\sum_{j=0}^{\frac{n}2-1}a_{2j+1}\omega_{\frac{n}2}^{kj}\)。
此时再根据\(\text{Theorem 2}\),我们可以写出\(A(\omega_n^k)\)和\(A(\omega_n^{k+\frac{n}2})\)的表示:
我们成功了!现在只需要分别求奇数项和偶数项的 DFT 就能求出来两个值了!运算量减少了一半!(可以证明这个过程的确是\(O(n\log n)\)的)
但是先别高兴得太早,我们还有一步:将运算完的点值表示转化回系数表示(毕竟大多数时候我们要的是乘积多项式的系数)。这时候应该怎么办呢?
Notice:由于证明较复杂且超出了高中的知识范围,建议从此处开始跳过直接看结论。
注意到我们求值的过程实际上就是计算了一个矩阵乘法:
而我们的任务就是求系数矩阵(假设叫做\(V\))的逆矩阵。
注意到这个矩阵是一个 Vandermonde 矩阵,对此,我们可以很容易地求出它的逆矩阵。
两个比较繁复的证明:
利用行列式及伴随矩阵
利用拉格朗日插值
然而最终的结果非常优美:设\(V=\{v_{ij}\}\),则\(V^{-1}=\frac 1n\{v_{ij}^{-1}\}\)。
Notice:现在你可以在此停止了,结论就在下方。
所以,我们只需要将 DFT 中\(\omega_n^k\)换成\(\omega_n^{-k}\)(体现为虚部取相反数),再将答案乘以\(\frac 1n\)就行了!
由此,我们就可以用一个函数来实现 DFT 和 IDFT 的过程了。
3.递归实现 FFT
一层层向下递归,求出 FFT :
void FFT(C *f,int len,int opt){//f是要进行DFT的数组,len是长度,opt是要进行的操作DFT/IDFT
if(len==1)return;
C *f0=f,*f1=f+(len>>1);
for(rg int i=0;i<len;i++)tmp[i]=f[i];
for(rg int i=0;i<(len>>1);i++){//按奇偶性分成两个多项式
f0[i]=tmp[i<<1],f1[i]=tmp[i<<1|1];
}
FFT(f0,len>>1,opt),FFT(f1,len>>1,opt);//分别进行FFT
C wn=C(cos(2*Pi/len),opt*sin(2*Pi/len)),w=C(1,0);//wn是本原单位根,w是wn的幂
for(rg int i=0;i<(len>>1);i++){
tmp[i]=f0[i]+w*f1[i];//按照上面推出来的式子进行计算
tmp[i+(len>>1)]=f0[i]-w*f1[i];
w=w*wn;
}
for(rg int i=0;i<len;i++)f[i]=tmp[i];
}
C++ STL 为我们提供了复数类,但是据说常数巨大,而手写复数类也不难写,所以还是建议大家手写:
struct C {
double re,im;
C(double _re=0.0,double _im=0.0){
re=_re,im=_im;
}
}f[N],g[N],tmp[N];
il C operator + (C a,C b){
return C(a.re+b.re,a.im+b.im);
}
il C operator - (C a,C b){
return C(a.re-b.re,a.im-b.im);
}
il C operator * (C a,C b){
return C(a.re*b.re-a.im*b.im,a.re*b.im+a.im*b.re);
}
而最终实现可以这么写:
FFT(f,len,1),FFT(g,len,1);
...//进行计算
FFT(f,len,-1);
4.迭代实现 FFT
注意到上面的实现方式需要进行大量递归,常数巨大(据说在洛谷会只有77分,但我实测能很宽松地通过),我们考虑如何优化常数。
这时候就需要拿出这张著名的图片了(注意下面最后两个框顺序反了):
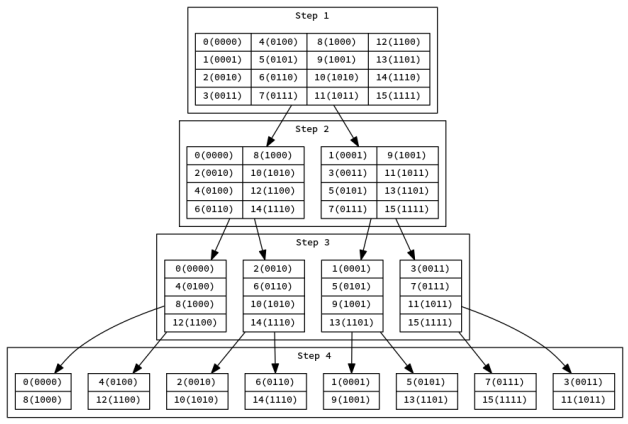
这是我们进行递归的顺序,大家观察一下二进制有什么发现?
可以发现,我们其实就是按照反转二进制排序之后依次分组的!如\(0000,1000,0100,1100\)倒过来就是\(0000,0001,0010,0011\)。
所以,我们可以将要进行 FFT 的数组按照反转二进制排序,然后直接迭代即可!
for(rg int i=1;i<len;i++){
r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));//求出i的反转二进制(其中l是二进制位数)
}
而我们不需要递归的 FFT 函数变成了这样:
void FFT(C *f,int len,int opt){
for(rg int i=0;i<len;i++){
if(i<r[i])swap(f[i],f[r[i]]);//排序
}
for(rg int i=2;i<=len;i<<=1){
int mid=i>>1;
C wn=C(cos(2*Pi/i),opt*sin(2*Pi/i));
for(rg int j=0;j<len;j+=i){
C w=C(1,0);
for(rg int k=0;k<mid;k++){
C z=f[j+k+mid]*w;
f[j+k+mid]=f[j+k]-z,f[j+k]=f[j+k]+z;
w=w*wn;
}
}
}
}
用时和内存都有了优化。
另外,关于 FFT 还有一个优化:三次变两次。实现方法是将多项式\(g\)放到多项式\(f\)的虚部,这时\(f^2\)的虚部除以二就是我们要的答案。这个方法也可以省去不少常数。
5.应用
FFT 的最大应用是优化多项式卷积的计算。所谓卷积其实就是多项式乘法,它的定义是:对于两个函数\(f(n),g(n)\),它们的卷积\((f*g)(n)=\sum_{i+j=n}f(i)g(j)\)。(就是个听起来挺nb的名字)
所以,当我们碰到一个恶心的式子时,可以尝试将其化为卷积的形式。
例题:洛谷P3338 [ZJOI2014]力
题目让我们求\(E_j=\sum_{i=1}^{j-1}\dfrac{q_i}{(i-j)^2}-\sum_{i=j+1}^{n}\dfrac{q_i}{(i-j)^2}\)的值,我们想办法将它化一化。
为了好看,我们设\(f_i=q_i,g_i=\dfrac{1}{i^2}\)。这时候原式变成了\(\sum_{i=1}^{j-1}f_ig_{j-i}-\sum_{i=j+1}^nf_ig_{i-j}\)。
我们优化一下上下界,令\(f_0=g_0=0\),有\(E_j=\sum_{i=0}^jf_ig_{j-i}-\sum_{i=j}^nf_ig_{i-j}\)。
发现第一项已经是卷积形式,我们来着重推一推第二项\(\sum_{i=j}^nf_ig_{i-j}\)。
运用和式中变量代换的技巧,这个式子就等于\(\sum_{i=0}^{n-j}f_{i+j}g_i\)。
这里还有一个常用的技巧,就是引入反转函数\(f'_i=f_{n-i}\)。此时原式变成了\(\sum_{i=0}^{n-j}f'_{n-j-i}g_i\),再代换一次就是\(\sum_{i=0}^mf'_{m-i}g_i\)。
我们把它化成了卷积形式,现在可以用 FFT 做了!
核心代码(代码里h[i]就是我们说的\(f'_i\)):
int main(){
Read(n);
for(rg int i=1;i<=n;i++){
cin>>f[i].re;h[n-i].re=f[i].re;
g[i].re=1.0/(1.0*i*i);
}
while(len<n+n+1)len<<=1,l++;
for(rg int i=1;i<len;i++){
r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
}
FFT(f,len,1),FFT(g,len,1),FFT(h,len,1);
for(rg int i=0;i<=len;i++)f[i]=f[i]*g[i],h[i]=h[i]*g[i];
FFT(f,len,-1),FFT(h,len,-1);
for(rg int i=1;i<=n;i++){
printf("%.3lf\n",(f[i].re-h[n-i].re)/len);
}
return 0;
}
6.总结
FFT 是多项式的基础算法,也是许多新手学多项式要过的第一关。理解了此处的知识,才能为之后的学习打下良好基础。
习题二:洛谷P3803 【模板】多项式乘法(FFT)
习题三:洛谷P1919 【模板】A*B Problem升级版(FFT快速傅里叶)

