[整理]网络流随记——下(应用举例)
前篇:最大流
中篇:费用流
\(\color{red}{Tips:Please\ read\ the\ above\ two\ articles\ first!}\)
0.概述
之前我们提到过,网络流的难点在于建模,所以本篇文章主要对网络流的各种奇奇怪怪的建模方式做一些粗浅的探讨,请确保你对网络流基础已经有了了解。
另外,本文不会涉及太多难题,如果觉得太简单,可以自行查找论文资料。
1.最大流的应用
例题一:洛谷P3191 [HNOI2007]紧急疏散EVACUATE
首先可以想到二分时间\(T\),然后就转化成了在规定时间内能不能撤离的问题。
题目中说到,每个时刻每个门只能对应一个人,不难想到将人和门连边,然后求最大匹配,若是所有人都能匹配上某个时刻的门,就说明撤离成功。
如图所示,设某个人最少需要花\(t\)的时刻到达一个门,那么可以如此连边:
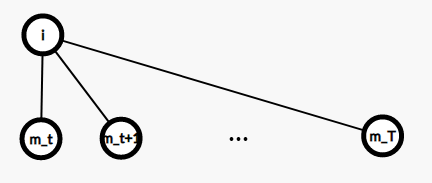
但是如果计算一下空间复杂度就会发现这样连边显然不行,于是我们采用一个常用的 trick :

这样,我们把每个时刻的门向下一个时刻连边,表示可以站着等,人到门只需要连一条边即可。于是我们就 A 掉了这个题。
总结:对于含有一一对应关系的题目,可以尝试转化为二分图匹配来求解。
例题二:洛谷P4311 士兵占领
这道题要求最小士兵数量,我们可以转化一下这个问题:每个士兵可以对一行或者一列产生贡献,我们需要让同时产生两个贡献的士兵最多(也就是最多可以删去多少多余的士兵)。
那么此时贡献为2的士兵一行最多有\(r_i\)个,一列最多有\(c_i\)个。我们可以考虑对每行每列分别建一个点,超级原点连每行(容量为\(r_i\)),每列连超级汇点(容量为\(c_i\)),行列之间连容量为1的边表示能放。
此时一条可行的流代表了一个贡献为2的士兵,答案就是最多要放的士兵数减去贡献为2的士兵。
总结:对于放置的个数有限制且一个放置有明确意义的题目,可以尝试转化为最大流来求解。
2.最小割的应用
例题三:洛谷P2057 [SHOI2007]善意的投票/[JLOI2010]冠军调查
这道题让我们求最小的冲突数,我们可以想到使用最小割来求解。
考虑如何表示一对朋友的选择:
设超级源点和超级汇点分别表示两种意愿,每个人连到自己的意愿(容量为1),朋友之间连双向边(容量为1)。
如图表示了两种情况下的选择(边上的字表示割掉此边的意义):
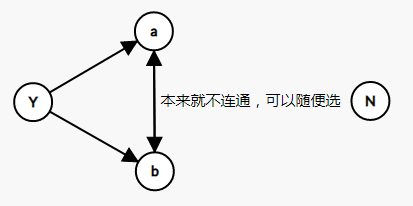

此时一个最小割就表示了一种选择方案。
总结:对于存在收益冲突的收益最大化/冲突最小化问题,可以尝试转化为最小割来求解。
例题四:洛谷P1646 [国家集训队]happiness
这道题也是做出选择使收益最大化类型的,我们可以考虑最小割:算出所有的收益,然后减去最小割。
发现最多同时涉及两个人的关系,我们可以分情况讨论:
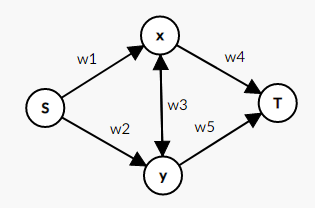
假设从超级源点连出来的边代表文科收益,连到超级汇点的边代表理科收益,两人之间的边代表共同收益,那么我们可以列出方程组表示不同情况下损失的收益(其中\(v_1,v_2\)分别代表同时选文、选理的收益):
解得
这样就解决了两人关系的处理,接下来再加上个人选文科或理科的收益即可。此时的一个割就代表了一种选科方案。
此题有一个细节:由于出现了分数,加边时需要乘二,在答案中减去时要除以二。
总结:对于存在两人关系的收益最大化题目,可以通过解方程求出边权,转化为最小割来求解。
3.费用流的应用
例题五:洛谷P3980 [NOI2008]志愿者招募
这道题初看可能毫无头绪,我们来尝试将其转化:一些志愿者工作,实际上就是另一些志愿者休假。
对于一个志愿者,他到了可以工作的那一天,要么开始连续工作,要么不工作继续颓。
那么我们可以尝试按天建图,每天向下一天连边\((i,i+1,-a_i,0)\)表示这一天至少\(a_i\)个志愿者不颓废,每个志愿者连一条边\((s_i,t_i+1,0,c_i)\)表示他可以花费\(c_i\)从\(s_i\)开始工作到\(t_i\)。
最终建出来的图大概是这样的:
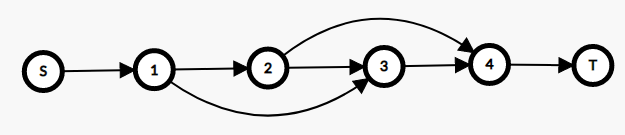
这样的话求最大流程序会在跑满免费的边之后自动用志愿者边填补空缺,同时也就求出了最小费用。
由于网络里不能有负流量边,我们把这些边都加上一个足够大的值(例如\(+\infty\)或\(\max a_i\)等)再跑费用流即可。
总结:对于有最小代价且有个数限制的题目,可以尝试转化为最小费用最大流来求解。
例题六:洛谷P4249 [WC2007]剪刀石头布
此题要求最多的三元环数量,不太好求。我们可以尝试将其转化为相反情况:求最少非环三元组数量。(也称之为补集转化)
可以发现此时的三个人一定是分别赢了2、1、0场,如果每个人分别赢了\(w_i\)场,那么他能构成的这种情况的数量就是\(\sum_i\binom{w_i}{2}=\sum_i\frac{w_i(w_i-1)}{2}\)。
对于建图,我们可以对未进行的比赛建点,再向比赛双方连边(容量均为1),每个选手向汇点连容量为\(n\)的边。可以发现此时一个一单位的流就代表了一个人的胜负情况。
那么我们把费用安到选手连汇点的边上,就可以用费用流解决啦!(并不)
我们发现\(\sum_i\frac{w_i(w_i-1)}{2}\)不是线性增长的,不能直接安到费用上,所以需要用到一个小技巧:拆边。
具体地说,发现\(\frac{w_i(w_i-1)}{2}\)可以拆成等差数列\(0+1+\cdots+w_i\)的形式,于是我们就把一条边拆成很多容量为1,费用为\(0,1,\cdots, w_i\)的边,这样的话就能满足题设条件了。
总结:此题用到的技巧主要有两个,一是答案不好直接求时进行补集转化,二是单位费用有变化时进行拆边。


