上接 https://www.cnblogs.com/juruo-zzt/p/15369446.html
设 F(x)=∑∞i=0xi,生成函数是形式幂级数,不考虑其收敛性。假设它收敛,那么有 (1−x)F(x)=1,即:
11−x=∞∑i=0xi
对上述公式求 k−1 阶导可得:
(k−1)!(1−x)k=∞∑i=0(i+k−1)k−1–––––xi
两边同时除以 (k−1)! 得:
1(1−x)k=∞∑i=0(k+i−1k−1)xi
范德蒙德卷积
∑i(ni)(mm−i)=(n+mn)
[xn](x+1)n(x+1)m=[xn](x+1)n+m=(n+mn)
上指标求和
a∑i=0(ib)=(a+1b+1)
[xa]11−x⋅xb(1−x)b+1=[xa]xb(1−x)b+2=(a+1b+1)
不知道叫什么的神秘公式
n−b∑i=a(ia)(n−ib)=(n+1a+b+1)
[xn]xa(1−x)a+1⋅xb(1−x)b+1=[xn]xa+b(1−x)a+b+2=(n+1a+b+1)
神秘公式 2
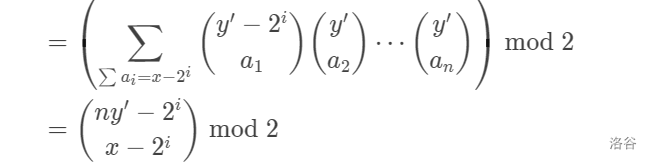
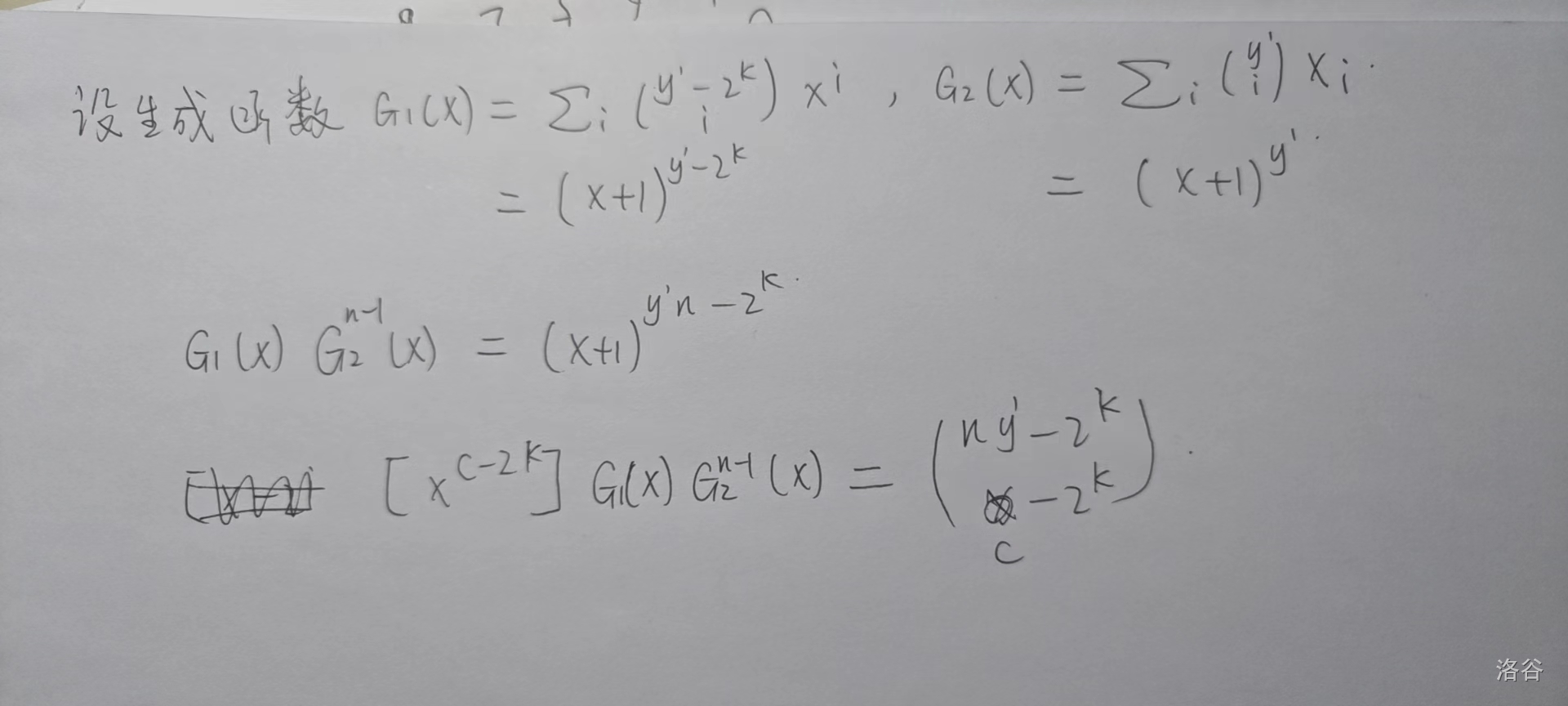
总的来说就是凑卷积形式
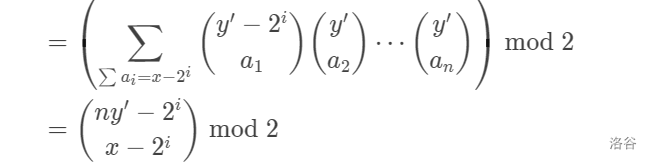
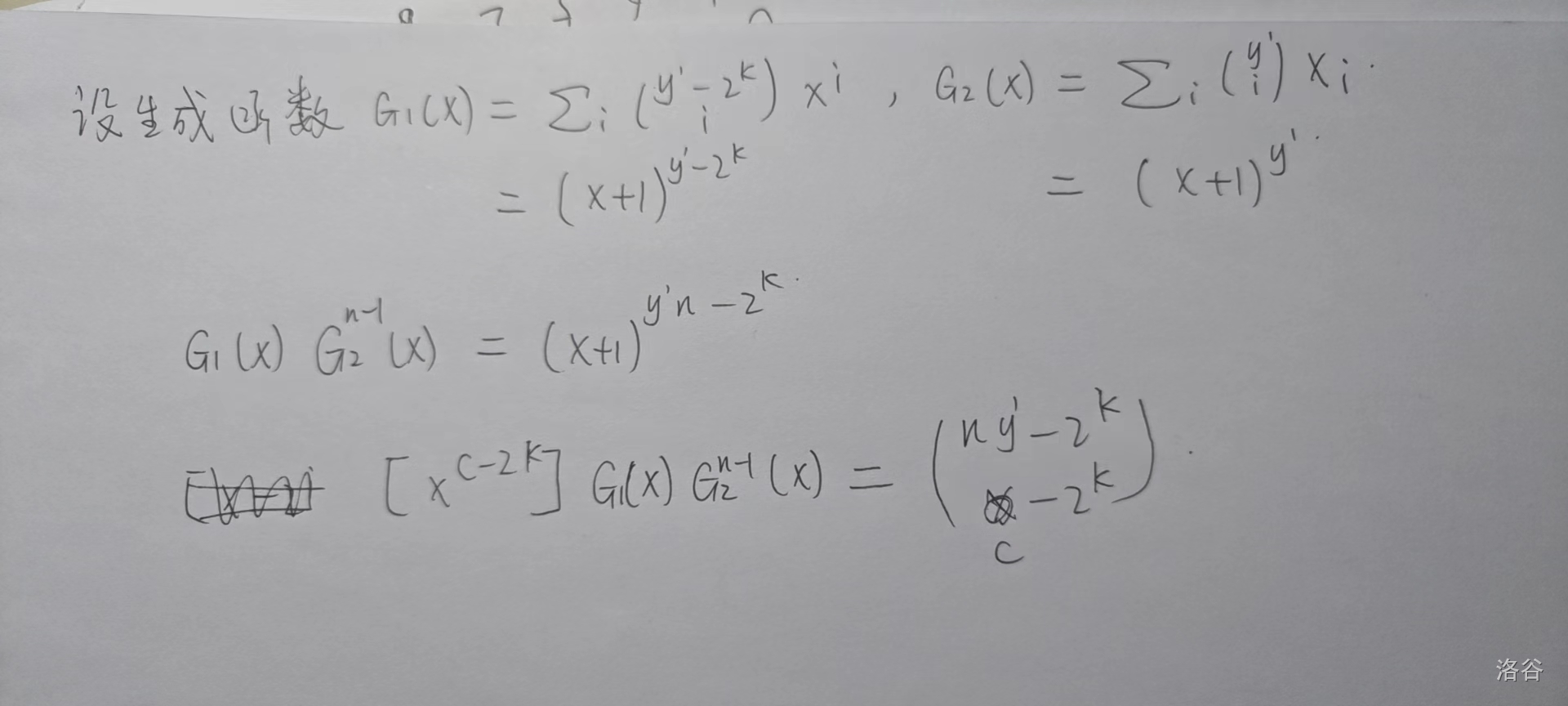
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】