CF *2700泛做
CF *2700 泛做
带星号的题代表还没更
CF961G Partitions
观察 \(W(S)=|S|\sum_{x\in S}w_x\),它可以看作是对于 \(S\) 的每个数都向集合内其他数(包括自己)贡献自己的 \(w\)。
每个数对自己的贡献是次数是 \(\begin{Bmatrix}n\\k\end{Bmatrix}\),对其他数的贡献是 \((n-1)\begin{Bmatrix}n-1\\k\end{Bmatrix}\),答案即:
CF1601D Difficult Mountain
bool cmp(node x,node y)
{
return max(x.s,x.a)==max(y.s,y.a)?x.s<y.s:max(x.s,x.a)<max(y.s,y.a);
}
*CF1572C Paint
待更新
CF1149C Tree Generator™
去掉匹配的括号之后,答案一定是形如 ))))))((( 这样的情况。
给 ( 赋 \(+1\) 的权,) 赋 \(-1\) 的权,那么答案就是一段区间批成两段,求后面的权值和减去前面的权值和的最大值,线段树维护即可。
大概要维护这些东西:
struct seg{
int sum,ans;
int lmx,lmn,rmx,rmn;
int lans,rans,lrans;
seg(){sum=ans=lmx=lmn=rmx=rmn=lans=rans=0;}
}t[N<<2];
CF938F Erasing Substrings
直接 dp 的话 dp 值是一个 string,这就寄上天啦,时间空间通通爆炸!!
考虑 \(f(i,j)=\mathtt{true}/\mathtt{false}\) 表示考虑当前 \(i\) 个字符没删,删除的 bitmask 状态是 \(j\),当前是否能够等于答案中的 \(t_{[1,i]}\),转移时带上字典序最小的条件即可,即:
for(int i=1;i<=n-(1<<k)+1;i++)
{
int mn=0x7fffffff;
for(int j=0;j<(1<<k);j++)if(f[i-1][j])mn=min(mn,(int)s[i+j]);
for(int j=0;j<(1<<k);j++)f[i][j]=f[i-1][j]&&s[i+j]==mn;
for(int j=0;j<(1<<k);j++)for(int l=0;l<k;l++)if(j&(1<<l))f[i][j]|=f[i][j^(1<<l)];
putchar(mn);
}
时间复杂度 \(\mathcal O(n^2\log n)\)。
CF1148F Foo Fighters
如果 \(\sum val_i<0\) 那么就全都取个反,下面只讨论 \(\sum val_i> 0\) 的情况。
把 \(mask_i\) 按照最高位从低到高排序,这样前面考虑的对后面考虑的没有影响。
维护一个 \(sum\) 表示考虑过的数的和。考虑每一位,先钦定这一位是 \(0\),然后加上对应的权值。如果此时 \(sum>0\) 那么就把这一位改成 \(1\),这么操作之后一定有 \(sum<0\)。
CF1617E Christmas Chocolates
性质:把每个值看作一个点,那么值域内所有值构成一棵树。
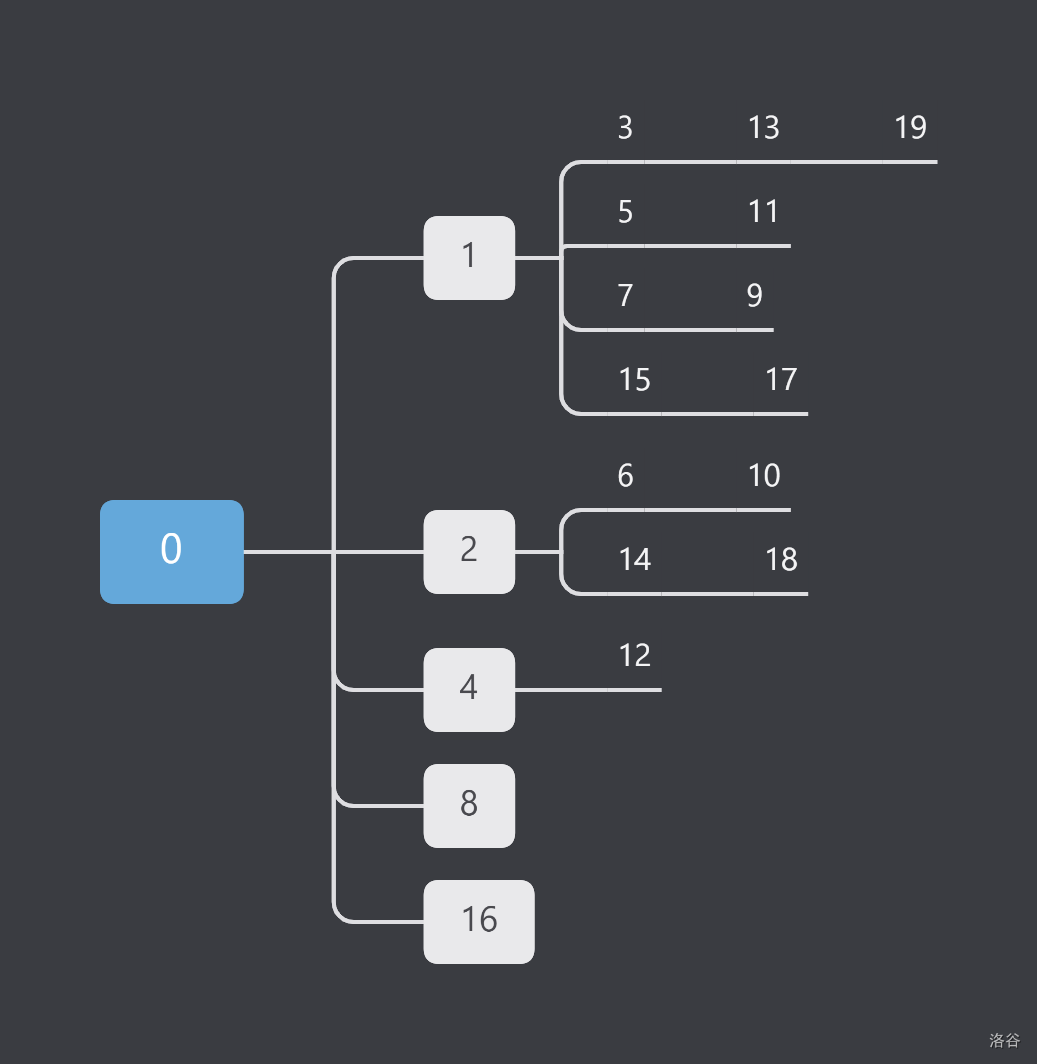
归纳可证。
考虑 \(dis(u,v)=dep_u+dep_v-dep_{\mathrm{lca}(u,v)}\)。可以发现 \(x\) 的深度是 \(\mathcal O(\log x)\) 级别的,那么这些量开个 map 暴力往祖先跳即可求得。
CF1421E Swedish Heroes
打表可知,\(2cnt^-+2cnt^+\equiv 1 \pmod 3\),且必须有两个数相邻且符号相等,那么 \(\mathcal O(CN)\) dp 即可,其中 \(C\) 是一个常数,根据实现可能等于 \(12\) 或者 \(24\) 等。
CF1408G Clusterization Counting
结论:如果从小到大排序加边,那么一个组是满足条件的当且仅当在加边过程中该组的点导出子图是一个团。
考虑 Kruskal 重构树,由于重构树的点代表连通块,所以所有满足条件的组在重构树上是一段连续的叶子节点,处理 dfs 序之后就是一段区间。
那么就可以直接 \(\mathcal O(n^2)\) dp 了。
*CF1285F Classical?
待更新
CF1519E Off by One
对于每个点,把他所能能够达到的两个 \(\tan\) 连边,那么两个点匹配就相当于删掉两条共点的边。
对于每个连通块,可以发现它的答案一定是 \(\lfloor|E|/2\rfloor\)。
如何构造方案?考虑求出连通块的任意一棵生成树,dfs 一遍,从叶子往上合并答案。对于一个点 \(i\),讨论其度数奇偶性:
- \(deg_i\bmod 2 = 0\),那父亲节点。
可以发现这一定能够达到上界 \(\lfloor |E|/2\rfloor\)。
CF1523E Crypto Lights
设 \(p_i\) 表示 \(i\) 次结束的概率,那么答案就是 \(\sum_{i=1}^n p_ii\)。考虑 \(\mathit{suf}_i=\sum_{j=i}^n p_i\),那么上式可以表示成 \(\sum_{i=1}^n \mathit{suf}_i\)。考虑 \(\mathit{suf}_i\) 的实际意义,就是前 \(i\) 次操作都满足条件的概率,这就是一个插板法,可以表示成 \({\binom{n-(k-1)(i-2)}{i-1}}/{\binom{n}{i-1}}\)
CF1325E Ehab's REAL Number Theory Problem
\(d(x)\le 7\) 等价于 \(\omega(x)\le 2\),那么把两个质因子建个边就是求图的最小环。
最小环肯定是没有办法直接求的,所以还要发掘性质。
令 \(A\) 为 \(a_i\) 值域,\(B=\sqrt{A}\),那么一个环一定带一个 \(\le B\) 的点,因为两个 \(>B\) 的无法连边。
所以枚举起点即可,\(\mathcal O(n\sqrt{A})\)。
CF995E Number Clicker
求 \(x^{-1}\) 的操作可以看作是在 \([0,p)\) 里面随机一个数,根据生日悖论,在比较少的次数内可以随出来两个相等的数,于是双向 BFS 即可。
CF1264E Beautiful League
注意到如果三个点 \(A,B,C\) 不是形如 \(A\to B,B\to C,C\to A\) 的形态的话,则一定有一个点入度为 \(2\),进而可以算出这样的三元组数量是 \(\sum_{i=1}^n \binom{\mathit{deg}_i}{2}\)。
要最大化合法三元组,就要最小化上式。这是一个代价为 \(w^2\) 的费用流,接下来就是典中典了,拆边即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号