20210603模拟赛总结
T1
是原题,CF475D。
注意到当一个区间 \([l,r]\) 当 \(l\) 固定、\(r\) 增大时 $\gcd $ 只有 \(\mathcal O(\log a_i)\) 种取值,直接讲这些取值都预处理出来即可。
#include<iostream>
using namespace std;
#define int long long
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
const int N=1e5+10;
map<int,int> cnt;
int gcd(int x,int y)
{
if(min(x,y)==0)return max(x,y);
return y==0?x:gcd(y,x%y);
}
int a[N],st[N][30],Log[N],n;
int query(int l,int r)
{
int x=Log[r-l+1];
return gcd(st[l][x],st[r-(1<<x)+1][x]);
}
void calc(int l)
{
int r=l;
while(r<=n)
{
int L=r,R=n,pos=0;
while(L<=R)
{
int mid=(L+R)/2;
if(query(l,mid)==query(l,r))pos=mid,L=mid+1;
else R=mid-1;
}
cnt[query(l,r)]+=pos-r+1;
r=pos+1;
}
}
signed main()
{
n=read();for(int i=1;i<=n;i++)st[i][0]=a[i]=read();
for(int j=1;(1<<j)<=n;j++)for(int i=1;i+(1<<j)-1<=n;i++)st[i][j]=gcd(st[i][j-1],st[i+(1<<(j-1))][j-1]);
for(int i=2;i<=n;i++)Log[i]=Log[i/2]+1;
for(int i=1;i<=n;i++)calc(i);
bool f=0;
int m=read();for(int i=1;i<=m;i++)printf("%lld\n",cnt[read()]);
return 0;
}
T2
构造 \(f_i\) 和序列 \(a_i\):
\[f_i=\begin{cases}0, &i=0\\10f_{i-1}+1,&0<i\le n\end{cases}\\
a_i\in[0,9],\sum_{i=0}^na_i=9
\]
则一个合法的解 \(a_0,a_1,\cdots,a_n\) 一定对应着一个合法的数,并且这个合法的数是 \(\sum_{i=0}^n f_ia_i\)。考虑 \(f_i\) 的贡献,根据插板法可知所有 \(f_i\) 的贡献 \(w\) 都是一样的,并且:
\[w=\sum_{i=0}^9i\binom{8+n-i}{n-1}
\]
但还是不够优秀,所以进入喜闻乐见的推式子环节……
引理:
\[\sum_{i=b}^a\binom{i}{b}=\binom{a+1}{b+1} \]其中 \(a\ge b\)。
证明:
(献上膝盖)
那么就可以推得:
\[\begin{align*}\sum_{i=0}^9i\binom{8+n-i}{n-1}&=\sum_{i=1}^9i\binom{8+n-i}{n-1}\\
&=\sum_{j=1}^9\sum_{i=j}^9\binom{8+n-i}{n-1}\\
&=\sum_{i=1}^9\binom{8+n-i+1}{n}\\
&=\binom{n+9}{n+1}\\
&=\binom{n+9}{8}
\end{align*}
\]
实际上就是在做下面这件事:

20230323 upd
这其实就是下面这个式子:
\[\sum_{i=a}^{n-b} \binom{i}{a}\binom{n-i}{b}=\binom{n+1}{a+b+1} \]证明:
\[[x^{n}]\frac{x^a}{(1-x)^{a+1}}\cdot\frac{x^b}{(1-x)^{b+1}}=[x^n]\frac{x^{a+b}}{(1-x)^{a+b+2}}=\binom{n+1}{a+b+1} \]
那么就得到了一个 \(\mathcal O(n)\) 的做法,但 \(n\le 10^{300}\),还是不够优秀。
注意到模数只有 \(19260817\),并且 \(f_{19260816}=f_0\),也就是说 \(19260816\) 是 \(f\) 的循环节,所以只需要计算单个循环节内的 \(f\) 即可。
代码待填,先贴个std:
#include<bits/stdc++.h>
#define mo 19260817
using namespace std;
string st;
long long p,q,ansn;
long long po(long long x,long long y)
{
long long z=1;
while(y)
{
if(y&1) z=(z*x)%mo;
x=(x*x)%mo;
y/=2;
}
return z;
}
long long c(long long x,long long y)
{
long long sum=1;
for(int i=1;i<=8;i++) sum=((sum*(x-i+1))%mo)*po(i,mo-2)%mo;
return sum;
}
int main()
{
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
cin>>st;
int l=st.length();
for(int i=0;i<l;i++)
{
p=p*10+st[i]-'0';
q=(q*10+p/mo)%mo;p%=mo;
}
for(long long i=1,j=0;i<=mo;i++)
{
j=(j*10+1)%mo;ansn=(ansn+j)%mo;
}
ansn=(ansn*q)%mo;
for(long long i=1,j=0;i<=p;i++)
{
j=(j*10+1)%mo;
ansn=(ansn+j)%mo;
}
cout<<(ansn*c(p+9+mo,8))%mo<<endl;
return 0;
}
T3
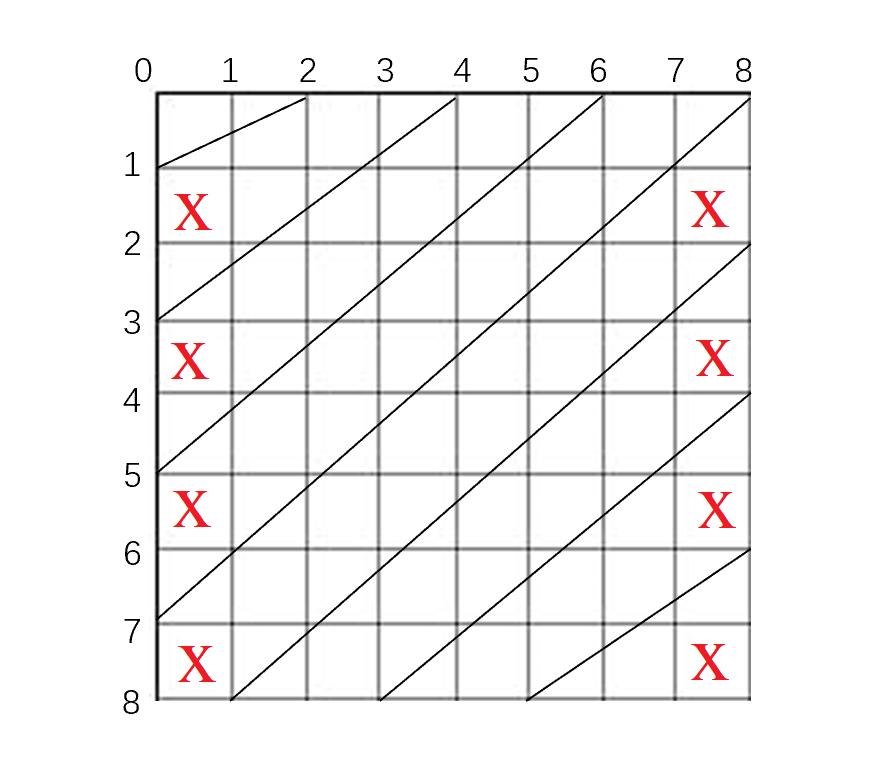
连 \((0,2)(1,0),(0,4)(3,0),\cdots\),这样只剩第一列和最后一列没有被覆盖,连上 \((0,0)(n,1),(0,n)(n,n-1)\) 即可。
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
int main()
{
int n=read();
printf("%d\n",n+1);
int x=1,y=2;
while(y<(n<<1))
{
if(x>n)printf("%d %d ",n,x-n);
else printf("%d %d ",x,0);
if(y>n)printf("%d %d\n",y-n,n);
else printf("%d %d\n",0,y);
x+=2,y+=2;
}
printf("%d %d %d %d\n",0,0,n,1);
printf("%d %d %d %d\n",0,n,n,n-1);
return 0;
}




