矩阵乘法

定义

设 \(A\) 是一个 \(n\times m\) 的矩阵，\(B\) 是一个 \(m\times p\) 的矩阵，那么 \(A\times B\) 的结果 \(C\) 中的元素为：

\[C_{i,j}=\sum_{i=1}^m A_{i,k}B_{k,j} \]

运算过程就是下面这样：

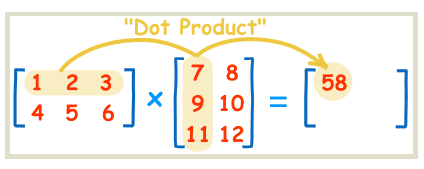
矩阵快速幂

由于矩阵满足结合律和分配律，所以可以使用快速幂。

斐波那契数列

一个经典的例子是 \(\mathcal O(\log n)\) 的时间复杂度求斐波那契数列的第 \(n\) 项。假设第 \(i\) 项为 \(f_i\)，那么有：

\[\left[ \begin{matrix} f_{i-1} &f_{i} \end{matrix} \right]\times \left[ \begin{matrix} 0 & 1\\ 1 & 1 \end{matrix} \right] =\left[\begin{matrix}f_i & f_{i+1}\end{matrix}\right] \]

答案就是求 \(\left[\begin{matrix}f_{0} & f_{1}\end{matrix}\right]\times\left[\begin{matrix}0 & 1\\1 & 1\end{matrix}\right]^{n-1}=\left[\begin{matrix}0 & 1\end{matrix}\right]\times\left[\begin{matrix}0 & 1\\1 & 1\end{matrix}\right]^{n-1}\) 的第 \(1\) 行第 \(2\) 列的数，对 \(\left[\begin{matrix}0 & 1\\1 & 1\end{matrix}\right]^{n-1}\) 快速幂求解即可做到 \(\mathcal O(\log n)\)。

求路径数量

给定一个邻接矩阵，每经过一条边的时间都是 \(1\)，求 \(T\) 秒之后 \(s\) 到 \(t\) 的路径数量。

考虑矩阵乘法的过程 \(C_{i,j}=\sum_{k=1}^nA_{i,k}B_{k,j}\)，实际上就是在将 \(i\sim k\) 和 \(k\sim j\) 的路径排列组合，所以直接求邻接矩阵的 \(T\) 次幂即可。

LOJ#10225. 迷路

边权变成了 \([1,9]\)，无法直接处理，那么将它拆为若干个边权为 \(1\) 的边。具体地，若有一条 \(u\) 到 \(v\) 边权为 \(w\) 的边，那么连 \((k-1)n+u\to kn+u\;(1\le k<w)\) 的边，再连一条 \(u+(w-1)n\to j\) 的边，边权都是 \(1\)，就可以直接跑矩阵快速幂了。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
inline int read()
{
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return x*f;
}
const int N=100;
typedef long long ll;
int n;
struct mat
{
	int a[N][N];
	void init(){for(int i=1;i<=n*9;i++)a[i][i]=1;}
	mat(){memset(a,0,sizeof(a));}
	mat operator *(const mat &x)const
	{
		mat ans;
		for(int k=1;k<=n*9;k++)
			for(int i=1;i<=n*9;i++)
				for(int j=1;j<=n*9;j++)
					ans.a[i][j]+=(ll)a[i][k]*x.a[k][j]%2009,ans.a[i][j]%=2009;
		return ans;
	}
};
mat qpow(mat a,int m)
{
	mat ans;ans.init();
	while(m)
	{
		if(m&1)ans=ans*a;
		a=a*a;
		m>>=1;
	}
	return ans;
}
char s[N][N];
int main()
{
	n=read();int t=read();
	mat x;
	for(int i=1;i<=n;i++)scanf("%s",s[i]+1);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			int cost=s[i][j]^48;
			if(!cost)continue;
			for(int k=1;k<cost;k++)x.a[i+(k-1)*n][i+k*n]=1;
			x.a[i+(cost-1)*n][j]=1;
		}
	}
	x=qpow(x,t);
	printf("%d",x.a[1][n]);
	return 0;
}