SSF信息社团1月训练题目整理

Hint：可以点击右下角的目录符号快速跳转到指定位置

上接：SSF信息社团12月训练题目整理
下接：SSF信息社团寒假训练题目整理（一）

Week 4（1.4 ~ 1.10）

1036C

数位 dp，直接套模板即可。

时间复杂度 \(\mathcal O(Td^2(n))\)，\(d(n)\) 表示 \(n\) 的位数。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
ll dp[30][30];
int digit[30];
int dfs(int step,int cnt,bool limit,bool zero)
{
	if(!step) return cnt<=3;
	if(!limit && !zero && ~dp[step][cnt]) return dp[step][cnt];
	int high=limit?digit[step]:9;
	ll ans=0;
	for(int i=0;i<=high;i++)
	{
		if(i){if(cnt<3) ans+=dfs(step-1,cnt+1,limit && i==digit[step],zero && !i);}
		else ans+=dfs(step-1,cnt,limit && i==digit[step],zero && !i);
	}
	if(!limit && !zero) dp[step][cnt]=ans;
	return ans;
}
ll sol(ll n)
{
	if(n==0) return 1ll;
	int cnt=0;
	while(n)
	{
		digit[++cnt]=n%10;
		n/=10;
	}
	memset(dp,-1,sizeof(dp));
	return dfs(cnt,0,true,true);
}
int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		ll l,r;
		scanf("%lld%lld",&l,&r);
		printf("%lld\n",sol(r)-sol(l-1));
	}
	return 0;
}

1043E

Link

先考虑 \(m=0\) 的情况。注意到两个人 \(x,y\) 的花费必定是在 \(a_x+b_y\) 和 \(a_y+b_x\) 中取最小的一个。对这两个式子做一下变形，容易得到若 \(a_x+b_y<a_y+b_x\)，则 \(a_x-b_x<a_y-b_y\)。所以我们对 \(n\) 个数对 \((a_1,b_1),(a_2,b_2),\cdots,(a_n,b_n)\) 按照 \(a_i-b_i\) 为关键字从小到大排序，可以发现，对于每一个 \(i\in[1,n]\) 来说，所有小于 \(i\) 的 \(j\) 与 \(i\) 的花费必定是 \(a_j+b_i\)，所有大于 \(i\) 的 \(j\) 与 \(i\) 的花费必定是 \(a_i+b_j\)。形式化地，第 \(i\) 个人的花费 \(c_i\) 可表示为 \(\left((i-1)b_i+\sum\limits_{j=1}^{i-1} a_j\right)+\left((n-i)a_i+\sum\limits_{j=i+1}^n b_j\right)\)，可以通过前缀和将所有 \(c_i\) 在 \(\mathcal O(n)\) 的时间内算出。

对于 \(m\not=0\) 的情况，在 \(\mathcal O(m)\) 的时间内将对应的 \(c_i\) 减去相应的花费即可。

#include<bits/stdc++.h>
using namespace std;
const int N=3e5;
struct node
{
	int x,y,pos;
	node() {}
	bool operator<(const node &rhs)const{return x-y<rhs.x-rhs.y;}
}a[N+10],b[N+10];
typedef long long ll;
ll sum1[N+10],sum2[N+10];
ll ans[N+10];
int main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++) 
	{
		scanf("%d %d",&a[i].x,&a[i].y);
		a[i].pos=i;
	}
	memcpy(b,a,sizeof(a));
	sort(a+1,a+n+1);
	for(int i=1;i<=n;i++)
	{
		sum1[i]=sum1[i-1]+a[i].x;
		sum2[i]=sum2[i-1]+a[i].y;
	}
	for(int i=1;i<=n;i++)
	{
		ans[a[i].pos]+=(ll)(i-1)*a[i].y+sum1[i-1];
		ans[a[i].pos]+=(ll)(n-i)*a[i].x+(sum2[n]-sum2[i]);
	}
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d %d",&x,&y);
		ans[x]-=min(b[x].x+b[y].y,b[x].y+b[y].x);
		ans[y]-=min(b[x].x+b[y].y,b[x].y+b[y].x);
	}
	for(int i=1;i<=n;i++) printf("%lld ",ans[i]);
    return 0;
}

1054D

Link

下文中 \(\operatorname{xor}\) 表示按位异或，\(\operatorname{xor}\limits _{i=j}^k a_i=a_j\operatorname{xor} a_{j+1}\operatorname{xor} \cdots \operatorname{xor} a_k\)，与 \(\sum\) 用法类似。

类似于前缀和，我们求出 \(\{a_i\}\) 的异或前缀和 \(\{s_i\}\)，\(s_i=\operatorname{xor}_{j=1}^i a_i\)。显然，若区间 \([l,r]\) 的异或和为 \(0\)，则 \(s_r\operatorname{xor} s_{l-1}=0\)，也就是 \(s_{l-1}=s_r\)。观察前缀和数组与题目的操作之间的关系，容易得到，若 \(a_i\) 取反，则 \(s_i\sim s_n\) 都会相应地取反。于是这道题就转化成了：给定 \(n\) 个数 \(s_i\)，对于每个数可以将其取反，求一种操作 \(\{s_i\}\) 中使得 \(s_i=s_j\) 的数对 \((i,j)\) 尽量少。我们可以得到一种贪心做法：将所有得到的数放到一个 STL map 或哈希表中，对于每个 \(s_i\)，若 map 中原数的数量小于取反之后的数量，将 \(s_i\) 放到 map 中并统计结果；反之，将 \(s_i\) 取反后的结果放到 map 中并统计结果。容易证明这样的贪心是对的。统计时需要特殊处理 \(s_i\) 或 \(s_i\) 取反后为 \(0\) 的情况。

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=2e5,MOD=1e6+7;
typedef long long ll;
int head[MOD+10],val[N+10],nxt[N+10],tot=0,cnt[N+10];
void ins(int x)
{
	int key=x%MOD;
	for(int i=head[key];i;i=nxt[i])
		if(val[i]==x)
		{
			cnt[i]++;
			return;
		}
	val[++tot]=x;
	nxt[tot]=head[key];
	head[key]=tot;
	cnt[tot]=1;
}
int query(int x)
{
	int key=x%MOD;
	for(int i=head[key];i;i=nxt[i])
		if(val[i]==x)
			return cnt[i];
	return 0;
}
int a[N+10];
int main() 
{
	int n,k;
	scanf("%d %d",&n,&k);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	ll ans=(ll)n*(n+1)/2ll;
	int sum=0;
	for(int i=1;i<=n;i++)
	{
		sum^=a[i]; 
		int x=sum,y=x^((1<<k)-1);
		int cx=query(x)+(x==0),cy=query(y)+(y==0);
		if(cx<cy)
		{
			ans-=cx;
			ins(x);
		}
		else
		{
			ans-=cy;
			ins(y);
		}
	}
	printf("%lld",ans);
	return 0;
}

1029D

Link

\(x,y\) 相连是 \(k\) 的倍数可以形式化地表示为：\(10^{d(y)}x+y\equiv0\pmod k\)，其中 \(d(y)\) 表示 \(y\) 的位数，例如 \(d(1234)=4\)。将这个式子变形，可以得到 \(10^{d(y)}\equiv -y\pmod k\)。于是我们就可以枚举 \(d(y)\)，算出 \((-y)\bmod k\)，使用 STL map 统计有多少个符合要求的 \(y\) 即可。

时间复杂度 \(\mathcal O(dn \log n)\)，\(d\) 表示位数，此题中为 \(10\)。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<map>
using namespace std;
#define int long long
int digit(int x)
{
	int ans=0;
	while(x)
	{
		ans++;
		x/=10;
	}
	return ans;
}
const int N=2e5;
int a[N+10];
int p[11];
signed main()
{
	int n,k;
	scanf("%lld %lld",&n,&k);	
	p[0]=1ll;
	for(int i=1;i<=10;i++) p[i]=p[i-1]*10%k;
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
	map<int,int> vis[11];//[d][mod]
	for(int i=1;i<=n;i++)
	{
		for(int d=1;d<=10;d++)
		{
			int kk=a[i]*p[d]%k;
			kk=-kk; kk=(kk+k)%k;
			vis[d][kk]++;
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		int dig=digit(a[i]);
		ans+=vis[dig][a[i]%k];
		if((a[i]*p[dig]+a[i])%k==0) ans--;
	}
	printf("%lld",ans);
	return 0; 
}

1031D

Link

又是一个没做出来的黄题，自闭了。

分析题目，最优答案一定是将路径前面几个格子不是 \(\texttt{a}\) 的字符改为 \(\texttt{a}\)。令 \(f(i,j)\) 表示从 \((1,1)\) 走到 \((i,j)\) 至少需要改变多少个字符才能使得走过来的路径上全都是 \(\texttt{a}\)，随便转移一下就好了。算出所有满足 \(f(i,j)\le k\) 的 \((i,j)\) 中 \(i+j\) 的最大值 \(m\)，并将其中所有满足 \(i+j=m\) 的 \((i,j)\) 存下来。答案的前 \(m-1\) 位一定全都是 \(\texttt{a}\)，其余的需要看这些 \((i,j)\) 走到 \((n,n)\) 能走出的字典序最小的字符串，BFS 即可。更具体地，将这些 \((i,j)\) 全都存到队列中，每次扩展新的点都求出新扩展的点中字典序最小的字符 \(c\)，将字符 \(=c\) 的点扩展即可，其他点一定不是最优的。

需要特判 \(k=0\) 的情况，不然会出一些奇奇怪怪的锅。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int N=2000,nxt[2][2]={0,1,1,0};
typedef pair<int,int> pii;
char a[N+10][N+10],ans[N*2+10];
int dp[N+10][N+10],tot=0;
int n,k;
bool vis[N+10][N+10];
int main()
{
	scanf("%d %d",&n,&k);
	for(int i=1;i<=n;i++) scanf("%s",a[i]+1);
	memset(dp,0x3f,sizeof(dp));
	dp[1][1]=(a[1][1]!='a');
	for(int i=1;i<=n;i++)
		for(int j=1+(i==1);j<=n;j++)
			dp[i][j]=min(dp[i-1][j],dp[i][j-1])+(a[i][j]!='a');
	vector<pii> v;
	int mx=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(k)
			{
				if(dp[i][j]<=k)
				{
					vis[i][j]=1;
					if(i+j>mx)
					{
						mx=i+j;
						v.clear();
						v.push_back(make_pair(i,j));
					}
					else if(i+j==mx) v.push_back(make_pair(i,j));
				}
			}
		}
	}
	if(k==0)
	{
		v.push_back(make_pair(1,1));
		vis[1][1]=1;
		ans[++tot]=a[1][1];
		mx=2;
	}
	queue<pii> que;
	for(int i=0;i<v.size();i++) que.push(v[i]);
	for(int Case=mx;Case<n+n;Case++)
	{
		v.clear();
		char Min='z';
		while(!que.empty())
		{
			pii head=que.front(); que.pop();
			for(int i=0;i<2;i++) 
			{
				int tx=head.first+nxt[i][0],ty=head.second+nxt[i][1];
				if(tx>n || ty>n || vis[tx][ty]) continue;
				if(a[tx][ty]<Min)
				{
					Min=a[tx][ty];
					vis[tx][ty]=1;
					v.clear();
					v.push_back(make_pair(tx,ty));
				}
				else if(a[tx][ty]==Min)
				{
					vis[tx][ty]=1; 
					v.push_back(make_pair(tx,ty));
				}
			}
		}
		ans[++tot]=Min;
		for(int i=0;i<v.size();i++) que.push(v[i]);

	}
	if(k)for(int i=1;i<mx;i++) putchar('a');
	for(int i=1;i<=tot;i++) putchar(ans[i]);
	return 0;
}

1041E

Link

构造题\(\times\) zzt必挂题\(\checkmark\)

Lemma1：对于一棵合法的树，所得到的所有 \(b_i\) 一定与 \(n\) 相同。

Proof1：显然。

Lemma2：对于一棵合法的树，一定也存在一个合法的链，使得二者形成的序列相同。

Proof2：令 \(n\) 为根节点，则此时 \(a_i\) 为子树内的最大编号。考虑将一个点下面的两条链合并，将所有边按照 \(a_i\) 排序，小的放在大的上面，得到一条新的链，容易证明这条链得到的 \(a_i\) 与之前的树相同。不断地将所有链合并，最终能得到一条 \(n\) 个点的链使得它得到的序列与原树一样。（感谢这篇博客的讲解）

有了 Lemma2，这道题就好办了。将 \(\{a_i\}\) 从小到大排序，若 \(a_i>a_{i-1}\)，就把 \(a_i\) 直接与上一个点连一条边并将 \(a_i\) 记为使用过；若 \(a_i=a_{i-1}\)，在区间 \([1,a_i-1]\) 里找一个未使用过的整数 \(j\)，将 \(j\) 与上一个点连一条边并标记为使用过。

至于判断无解，有两种情况，一种是 \(\exists i\in[1,n],b_i\not=n\)，一种是构造过程中找不到合法的 \(j\)，判一下就好了。

#include<bits/stdc++.h>
using namespace std;
const int N=1000;
int a[N+10];
bool vis[N+10];
typedef pair<int,int> pii;
pii ans[N+10];
int main()
{
	int n;
	scanf("%d",&n);
	bool flag=1;
	for(int i=1;i<n;i++)
	{
		int y;
		scanf("%d %d",&a[i],&y);
		if(y!=n) 
		{
			flag=0;
			break;
		}
	}
	if(!flag)
	{
		printf("NO");
		return 0;
	}
	sort(a+1,a+n);
	int tot=0;
	int pre=-1;
	for(int i=1;i<n;i++)
	{
		if(a[i]!=a[i-1])
		{
			if(i>1) ans[++tot]=make_pair(pre,a[i]);
			vis[a[i]]=1;
			pre=a[i]; 
		}
		else
		{
			bool flag1=0;
			for(int j=1;j<a[i];j++)
			{
				if(!vis[j])
				{
					flag1=1;
					vis[j]=1;
					ans[++tot]=make_pair(pre,j);
					pre=j;
					break;
				}
			}
			if(!flag1) 
			{
				flag=0;
				break;
			}
		} 
	}
	if(flag)
	{
		printf("YES\n");
		for(int i=1;i<=tot;i++) printf("%d %d\n",ans[i].first,ans[i].second);
		printf("%d %d",pre,n);
	}
	else printf("NO");
	return 0;
}

1032D

Link

看起来是一个神仙计算几何，实际上只是一个弱智题~~只不过没做出来~~。

结论：如果最短路径经过直线，那么直线上与 \(A(x_1,y_1)\) 相连的点要么 \(x\) 轴坐标为 \(x_1\) 要么 \(y\) 轴坐标为 \(y_1\)，\(B\) 同理。证明：（自己口胡的，欢迎 hack）

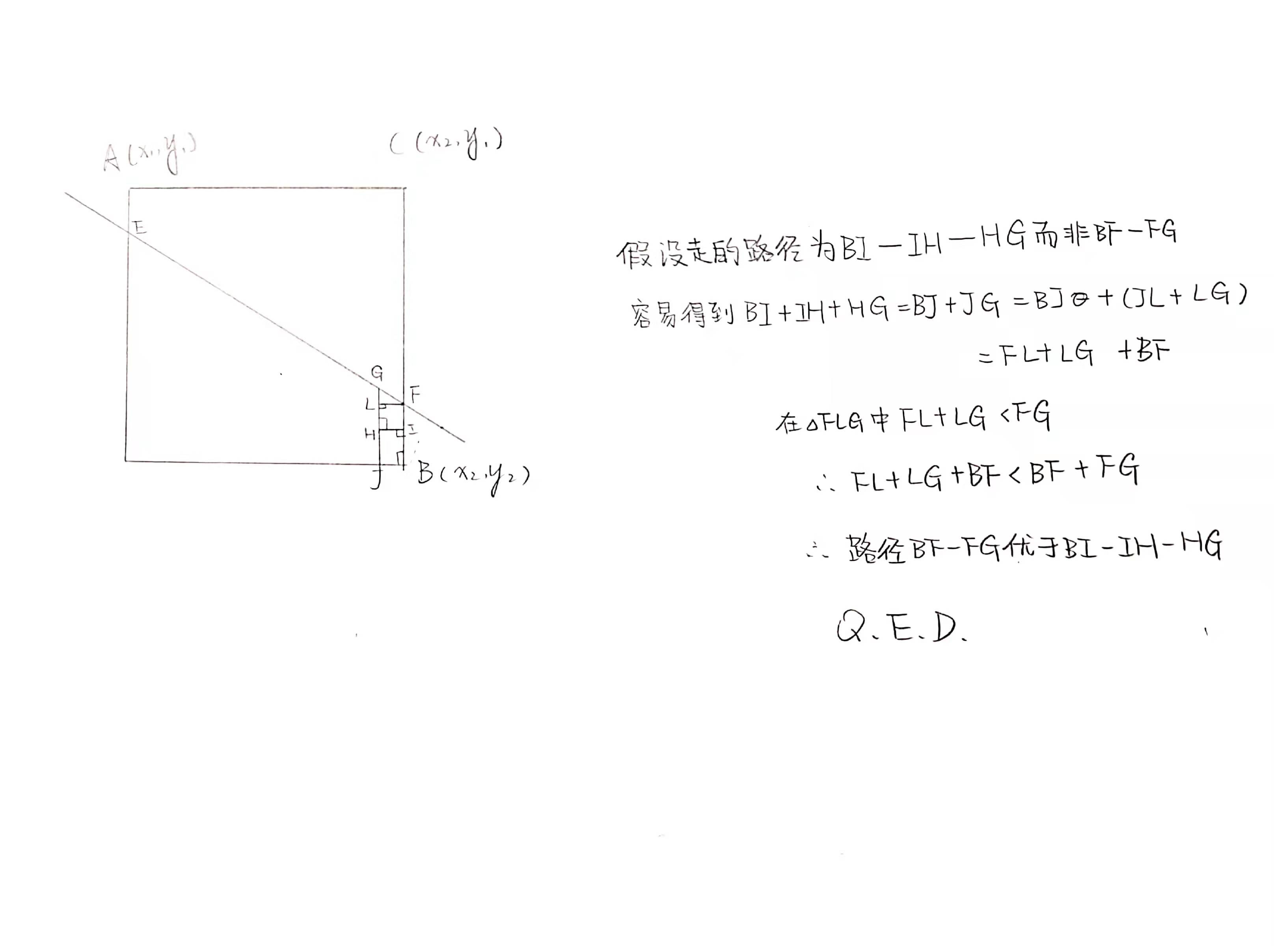
于是就可以与分别处理出直线上 \(x\) 轴坐标、\(y\) 轴坐标与 \(A\) 相同的点 \(E_1,E_2\)，直线上 \(x\) 轴坐标、\(y\) 轴坐标与 \(B\) 相同的点 \(E_3,E_4\)，枚举是最终是哪两个点就好了。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
double a,b,c;
double X1,X2,Y1,Y2;
// ax + by + c = 0
// ax = -by - c  ===>  x = (-by - c) / a
// by = -ax - c  ===>  y = (-ax - c) / b 
double getx(double y) {return (-b*y-c)/a;}
double gety(double x) {return (-a*x-c)/b;}
struct point
{
	double x,y;
	point(){}
	point(double xx,double yy) 
	{
		x=xx;
		y=yy;
	}
};
double dis(point x,point y)
{
	return fabs(X1-x.x)+fabs(Y1-x.y)+fabs(X2-y.x)+fabs(Y2-y.y)
	+ sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));
}
int main()
{
	scanf("%lf%lf%lf",&a,&b,&c);
	scanf("%lf%lf%lf%lf",&X1,&Y1,&X2,&Y2);
	point E1=point(getx(Y1),Y1),E2=point(X1,gety(X1)),//A
	E3=point(X2,gety(X2)),E4=point(getx(Y2),Y2);//B
	double ans=fabs(X1-X2)+fabs(Y1-Y2);
	ans=min(ans,min(min(dis(E1,E3),dis(E1,E4)),min(dis(E2,E3),dis(E2,E4))));
	printf("%.7lf",ans);
	return 0;
}

Week 5（1.11 ~ 1.17）

1398D

Link

考虑只有两种颜色的情况。由排序不等式可知，将较大的木棍与较大的木棍组合一定是最优的。将两个数组从大到小排序即可。

对于三种颜色的情况，同样将三个数组从大到小排序，与两种颜色的情况不同的是我们需要决策从哪两个颜色中取木棍，dp 即可。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=200;
int r[N+10],g[N+10],b[N+10];
ll dp[N+10][N+10][N+10];
// dp[r][g][b]
// the maximum total area that can be obtained by taking r largest red sticks,
// g largest green sticks and b largest blue sticks.
bool cmp(int a,int b) {return a>b;}
int main()
{
	int R,G,B;
	scanf("%d %d %d",&R,&G,&B);
	for(int i=1;i<=R;i++) scanf("%d",&r[i]);
	for(int i=1;i<=G;i++) scanf("%d",&g[i]);
	for(int i=1;i<=B;i++) scanf("%d",&b[i]);
	sort(r+1,r+R+1,cmp);
	sort(g+1,g+G+1,cmp);
	sort(b+1,b+B+1,cmp);
	ll ans=0;
	for(int i=0;i<=R;i++)
	{
		for(int j=0;j<=G;j++)
		{
			for(int k=0;k<=B;k++)
			{
				if((bool)i + (bool)j + (bool)k < 2) continue;
				if(i && j) dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-1][k]+r[i]*g[j]);
				if(i && k) dp[i][j][k]=max(dp[i][j][k],dp[i-1][j][k-1]+r[i]*b[k]);
				if(j && k) dp[i][j][k]=max(dp[i][j][k],dp[i][j-1][k-1]+g[j]*b[k]);
				ans=max(ans,dp[i][j][k]);
			}
		}
	}
	printf("%lld",ans);
	return 0;
}

1401D

Link

对于每一条边，预处理出所有路径中这条边被经过的次数 \(v_i\)，若放在这条边上的权值为 \(w_i\)，不难得出答案即为 \(\sum\limits_{i=1}^{n-1} v_iw_i\)。若 \(m\le n-1\)，由排序不等式，将最大的 \(m\) 个质因子放在 \(v_i\) 最大的 \(m\) 条边即可；若 \(m>n-1\)，将最小的 \(n-2\) 个 \(p_i\) 放到 \(v_i\) 最小的 \(n-2\) 条边上，其余都放到 \(v_i\) 最大的边上即可。容易证明这样做是正确的。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define int long long 
using namespace std;
const int N=1e5,MOD=1e9+7,M=6e4;
int head[N+10],ver[N*2+10],nxt[N*2+10],tot=1; 
int sz[N+10];
void add(int x,int y)
{
	ver[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
void dfs(int x,int fa)
{
	sz[x]=1;
	for(int i=head[x];i;i=nxt[i])
	{
		int y=ver[i];
		if(y==fa) continue;
		dfs(y,x);
		sz[x]+=sz[y];
	}
}
int val[N+10],p[M+10];
int n,m;
void dfs1(int x,int fa)
{
	for(int i=head[x];i;i=nxt[i])
	{
		int y=ver[i];
		if(y==fa) continue;
		val[i/2]=sz[y]*(n-sz[y]);
		dfs1(y,x);
	}
}
void sol()
{
	memset(head,0,sizeof(head));tot=1;
	scanf("%lld",&n);
	for(int i=1;i<n;i++)
	{
		int x,y;
		scanf("%lld %lld",&x,&y);
		add(x,y);
		add(y,x);
	}
	dfs(1,-1);
	dfs1(1,-1);
	sort(val+1,val+n,greater<int>());
	scanf("%lld",&m);
	for(int i=1;i<=m;i++) scanf("%lld",&p[i]);
	sort(p+1,p+m+1,greater<int>());
	int ans=0;

	// puts("sz:");
	// for(int i=1;i<=n;i++) printf("%lld ",sz[i]);
	// puts("\np:"); 
	// for(int i=1;i<=m;i++) printf("%lld ",p[i]);
	if(m<=n-1)
	{
		// printf("condition one\n");
		for(int i=1;i<=m;i++)
		{
			ans+=val[i]%MOD*p[i]%MOD;
			ans%=MOD;
		}
		for(int i=m+1;i<=n-1;i++) 
		{
			ans+=val[i];
			ans%=MOD;
		}
	}
	else
	{
		for(int i=2;i<=n-1;i++) 
		{
			ans+=(val[i]%MOD*p[m-n+i+1]%MOD);
			ans%=MOD;
		}
		for(int i=1;i<=m-n+2;i++) 
		{
			val[1]%=MOD;
			val[1]*=p[i];
			val[1]%=MOD;
		}
		ans+=val[1];
		ans%=MOD;
	}
	printf("%lld\n",ans);
}
signed main()
{
	int T;
	scanf("%lld",&T);
	while(T--) sol();
	return 0;
}

1402A

Link

感谢这篇题解和 lht 的讲解。

令 \(f(x)=\mathrm C_{x+1}^2\)，不难看出答案即为：

\[\sum\limits_{i=1}^n f(w_i)f(h_i) + \sum\limits_{1\le i<j\le n} w_iw_jf(\min\limits_{k=i}^n\{h_k\}) \]

左边的式子可以 \(\mathcal O(n)\)，但右边的式子暴力统计是 \(\mathcal O(n^2)\) 的，需要对其进行优化。注意到 \(\min\limits_{k=i}^n\{h_k\}\) 在一段区间内是一样的，所以我们可以用单调栈求出对于每一个 \(h_i\)，\(\min\) 值为 \(h_i\) 的长度最大的 \([l_i,r_i]\)。\([l_i,r_i]\) 及其子区间对于答案的贡献分为三部分：\(h_i\) 在中间的、\(h_i\) 在左端点的和 \(h_i\) 在右端点的，写成式子分别是：

\[f(h_i)\times\sum\limits_{j=l_i}^{i-1} w_j\times \sum\limits_{j=i+1}^{r_i} w_j\\ f(h_i)\times w_i\times \sum\limits_{j=i+1}^{r_i} w_j\\ f(h_i)\times w_i\times \sum\limits_{j=1}^{i-1} w_j\]

预处理 \(w_i\) 的前缀和可以做到 \(\mathcal O(n)\) 计算。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define int long long 
const int N=1e5,MOD=1e9+7;
int l[N+10],r[N+10],w[N+10],h[N+10];
int st[N+10],top,sum[N+10],n;
void init()
{
	st[++top]=1;
	for(int i=2;i<=n;i++) 
	{
		while(top && h[st[top]]>h[i]) r[st[top--]]=i-1;
		st[++top]=i;
	}
	while(top) r[st[top--]]=n;

	memset(st,0,sizeof(st));
	st[++top]=n;
	for(int i=n-1;i;i--)
	{
		while(top && h[st[top]]>=h[i]) l[st[top--]]=i+1;
		st[++top]=i;
	}
	while(top) l[st[top--]]=1;
}
int f(int x) {return x*(x+1)%MOD*500000004%MOD;}
signed main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++) scanf("%lld",&h[i]);
	for(int i=1;i<=n;i++) 
	{
		scanf("%lld",&w[i]);
		sum[i]=sum[i-1]+w[i];sum[i]%=MOD;
	}
	init();
	// for(int i=1;i<=n;i++) printf("[%lld, %lld]\n",l[i],r[i]);
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		ans+=f(w[i])*f(h[i])%MOD;ans%=MOD;
		ans+=f(h[i])*((sum[i-1]-sum[l[i]-1]+MOD)%MOD)%MOD
		*((sum[r[i]]-sum[i]+MOD)%MOD)%MOD;ans%=MOD;
		ans+=f(h[i])*w[i]%MOD*((sum[i-1]-sum[l[i]-1]+MOD)%MOD)%MOD;ans%=MOD;
		ans+=f(h[i])*w[i]%MOD*((sum[r[i]]-sum[i]+MOD)%MOD)%MOD;ans%=MOD;
	}
	printf("%lld",ans);
	return 0;
}

1409E

Link

\(y\) 坐标啥用没有。

对于每个 \(i\)，算出以它为右端点最多能接多少个点，记作 \(pre_i\)；类似地，算出以它为左端点最多能借助多少个点，记作 \(suf_i\)。令 \(suf_{n+1}=pre_1=0\)，答案即为 \(pre_{i-1}+suf_i\) 的最大值。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int N=2e5;
int a[N+10],pre[N+10],suf[N+10];
int max1[N+10],max2[N+10]; 
int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{ 
		memset(pre,0,sizeof(pre));
		memset(suf,0,sizeof(suf));
		memset(max1,0,sizeof(max1));
		memset(max2,0,sizeof(max2));
		int n,k;
		scanf("%d%d",&n,&k);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		for(int i=1;i<=n;i++)
		{
			int hello;
			scanf("%d",&hello);
		}
		sort(a+1,a+n+1);
		for(int i=1;i<=n;i++)
		{
			int l=1,r=i,ans=0;
			while(l<=r)
			{
				int mid=(l+r)/2;
				if(a[mid]>=a[i]-k)
				{
					ans=mid;
					r=mid-1;
				}
				else l=mid+1;
			}
			pre[i]=i-ans+1;
			l=i;r=n;ans=0;
			while(l<=r)
			{
				int mid=(l+r)/2;
//				printf("mid:%d\n",mid);
				if(a[mid]<=a[i]+k)
				{
					ans=mid;
					l=mid+1;
				}
				else r=mid-1;
			}
			suf[i]=ans-i+1;
		}
//		for(int i=1;i<=n;i++) printf("pre[i]:%d, suf[i]:%d\n",pre[i],suf[i]);
		for(int i=1;i<=n;i++)
		{
			max1[i]=max(max1[i-1],pre[i]);
			max2[n-i+1]=max(max2[n-i+2],suf[n-i+1]);
		}
		int ans=0;
		for(int i=1;i<=n+1;i++) ans=max(ans,max1[i-1]+max2[i]);
		printf("%d\n",ans);
	} 
	return 0;
}

1420D

Link

将线段按照左端点为第一关键字、右端点为第二关键字排序，从 \(1\) 到 \(n\) 枚举每个线段并计算前面有多少个线段与之重合，记作 \(m\)，若 \(m\ge k-1\)，将答案累加 \(\mathrm C_{m}^{k-1}\) 即可。至于为什么是 \(k-1\) 而不是 \(k\)，这是因为为了避免重复计算，我们令 \(i\) 必选，前 \(i-1\) 个线段都没有选过 \(i\)，\(n\) 个线段下来就不会重复计算。

计算组合数需要预处理阶乘和阶乘逆元。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define int long long
const int N=3e5,M=N*2,MOD=998244353;
struct segment
{
	int l,r;
	bool operator<(const segment&x)const{return l==x.l?r<x.r:l<x.l;} 
}a[N+10];
int n,m,c[M+10];
void modify(int x,int d) {for(;x<=m;x+=x&-x) c[x]+=d;}
int query(int x)
{
	int ans=0;
	for(;x;x-=x&-x) ans+=c[x];
	return ans;
}
int t[M+10];

int p[M+10],inv[M+10];
int qpow(int a,int nn)
{
	a%=MOD;int ans=1;
	while(nn)
	{
		if(nn&1) ans=ans*a%MOD;
		a=a*a%MOD;
		nn>>=1;
	}
	return ans;
}
void init()
{
	p[0]=inv[0]=1;
	for(int i=1;i<=M;i++)
	{
		p[i]=p[i-1]*i%MOD;
		inv[i]=qpow(p[i],MOD-2);
	}
}
int C(int nn,int mm) {return p[nn]*inv[mm]%MOD*inv[nn-mm]%MOD;}

signed main()
{
	int k;
	scanf("%lld %lld",&n,&k);
	for(int i=1;i<=n;i++) 
	{
		scanf("%lld %lld",&a[i].l,&a[i].r);
		t[i*2-1]=a[i].l;
		t[i*2]=a[i].r;
	}
	sort(t+1,t+n*2+1);
	sort(a+1,a+n+1);
	m=unique(t+1,t+n*2+1)-t-1;
	for(int i=1;i<=n;i++)
	{
		a[i].l=lower_bound(t+1,t+m+1,a[i].l)-t;
		a[i].r=lower_bound(t+1,t+m+1,a[i].r)-t;
	}
	init();
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		int tmp=query(m)-query(a[i].l-1);
		if(tmp>=k-1) ans=(ans+C(tmp,k-1))%MOD;
		modify(a[i].r,1);
	}
	printf("%lld",ans);
	return 0;
}

1426E

Link

感谢这篇题解，本文证明源自这里。

最大值很容易求，将石头尽量与对方的剪刀匹配、剪刀尽量与对方的布匹配、布尽量与对方的石头匹配即可，答案为 \(\min(a_1,b_2)+\min(a_2,b_3)+\min(a_3,b_1)\)。

对于最小值，答案为 \(n-\min(a_1,n-b_2)-\min(a_2,n-b_3)-\min(a_3,n-b_1)\)，即用石头与对方的非剪刀匹配、见到尽量与对方的非布匹配、布尽量与对方的非石头匹配，这样不会影响答案。简要证明一下，当且仅当类似 \(a_1 >b_3\) 且 \(a_2>b_2\) 的情况下会影响答案，而 \(a_1+a_2\le b_1+b_2+b_3\)，所以这种情况不会发生。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    scanf("%d",&n);
    int a1,a2,a3,b1,b2,b3;
    scanf("%d %d %d %d %d %d",&a1,&a2,&a3,&b1,&b2,&b3);
    printf("%d %d",n-min(a1,n-b2)-min(a2,n-b3)-min(a3,n-b1),min(a1,b2)+min(a2,b3)+min(a3,b1));
    return 0;
}

1442A

Link

看到区间修改，于是想到差分。令 \(a_0=0\)，构造差分数组 \(c_i=a_i-a_{i-1}\)，此时前 \(k\) 个数递减在差分数组中对应的就是 \(c_1\gets c_1-1\) 同时 \(c_{k+1}\gets c_{k+1}+1\)，后 \(k\) 个数递减就是 \(c_{n-k+1}\gets c_{n-k+1}-1\)，这样就从 \(a_i\) 的区间修改变成了 \(c_i\) 的单点修改。

考虑每一个 \(1<i\le n\) 的 \(c_i\)，若 \(c_i>0\)，我们可以使用 \(c_i\) 次第二个操作将其变为 \(0\)；若 \(c_i<0\)，需要使用 \(-c_i\) 次操作一让他变为 \(0\)，但操作一的副作用：\(c_1\) 也会减一。若 \(c_1\) 变成了负数，之后无论怎样操作也无法将其变为 \(0\)，此时无解。将所有 \(<0\) 的 \(c_i\) 的相反数累加，如果小于等于 \(c_1\) 有解，反之无解。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=30000;
int a[N+10],n,c[N+10];
int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&n);
		for(int i=1;i<=n;i++) 
		{
			scanf("%d",&a[i]);
			c[i]=a[i]-a[i-1];
		}
		int sum=0;
		for(int i=2;i<=n;i++)
			if(c[i]<0) sum+=-c[i];
		printf(sum<=c[1]?"YES\n":"NO\n");
	}
	return 0;
}

Week 6（1.18 ~ 1.24）

~~期末考试。~~ 考完了，复活了。

1088D

Link

This is an interactive problem!

开幕雷击

感谢这篇题解www

从高向低确定每个数位，确定一个数位后每次询问都 \(\operatorname{xor}\) 一下已确定的数位，这样每次确定的都能是「最高位」。每次对每个最高位都询问 0 1 和 1 0，会有下面三种返回结果：

先 -1 再 1，此时可以确定 \(a,b\) 的最高位都是 \(1\)；
先 -1 再 1，此时可以确定 \(a,b\) 的最高位都是 \(0\)；
两次返回的结果相同，此时可以确定 \(a,b\) 最高位不同。

情况三不太好确定，但实际上前面的处理的情况三我们都可以确定之后 \(a\) 和 \(b\) 的大小，用一个 bool 即可。至于最开始的情况三如何处理，可以问一次 0 0，这样就可以确定一开始的 \(a\) 和 \(b\) 的大小。总共的次数是 \(61\) 次，符合要求。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int main()
{
	int a=0,b=0;
	cout<<"? 0 0"<<endl;
	int f;
	cin>>f;
	for(int i=29;~i;i--)
	{
		int a1,a2;//answer1, answer2
		cout<<"? "<<(a|(1<<i))<<" "<<b<<endl;
		cin>>a1;
		cout<<"? "<<a<<" "<<(b|(1<<i))<<endl;
		cin>>a2;
		if(a1==-1 && a2==1)
		{
			a|=(1<<i);
			b|=(1<<i);
		}
		else if(a1==a2)
		{
			if(f>=1) a|=(1<<i);
			else b|=(1<<i);
			f=a1;
		}
	}
	cout<<"! "<<a<<" "<<b<<endl;
	return 0;
}

1083B

Link

如果把字符串都放到 Trie 树里，可以发现题目就变成了如何插入字符串能使得 Trie 树中的节点数最多。容易看出题目给出的两个串是一定要选的，不选的情况一定能够转换成选的情况。\(1\sim k\) 枚举层数，如果当前一层的节点数量 \(\le k\)，那么这一层都能选，否则选择 \(k\) 个。每层节点数量即为上一层的节点数量 \(\times 2\)，若题目给出的第一个串的当前一位为 \(\texttt{b}\)，数量减一；同理，若给出的第二个串的当前一位为 \(\texttt{a}\)，数量减一。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define int long long
const int N=5e5;
char a[N+10],b[N+10];
signed main()
{
	bool flag=0;
	int n,k;
	scanf("%lld%lld",&n,&k);
	scanf("%s%s",a+1,b+1);
	int ans=0,p=1;
	for(int i=1;i<=n;i++)
	{
		if(!flag)p*=2;
		p-=(a[i]=='b')+(b[i]=='a');
		if(p>k) flag=1;
		if(flag) ans+=k;
		else ans+=p;
	}
	printf("%lld",ans);
	return 0;
}

1082E

Link

一个性质：设选择的线段为 \([l,r]\)，那么一定有 \(a_l=a_r\)，因为如果不等，将一个端点挪到 \([l,r]\) 一个点使得 \(a_l=a_r\) 此时取的的值一定比原来的值更优。

让所有的 \(a_i\) 都变成 \(a_i-c\)，此时题目就变成了区间加一个数使得值为 \(0\) 的数最多。令 \(sum_i\) 表示前 \(i\) 个数中值为 \(0\) 的数的个数，\(sumk_i\) 表示前 \(i\) 个数中值为 \(a_i\) 的数的个数，那么我们要找到的就是最大的 \(sum_{l-1}+(sumk_r-sumk_{l-1})+sum_n-sum_r\)。将式子做一下变形，可以得到 \((sum_{l-1}-sumk_{l-1})+(sum_n-sum_r+sumk_r)\)。枚举 \(r\)，右面括号里的数就都成为了定值，只需要找到最大的 \(sum_{l-1}-sumk_{l-1}\)。因为需要保证 \(a_l=a_r\)，需要在枚举 \(r\) 的过程中将左边括号内的东西存在 STL unordered_map 中再取最大值。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<unordered_map>
using namespace std;
const int N=5e5;
int a[N+10],sum[N+10],sumk[N+10],f[N+10];
int main()
{
	int n,c;
	unordered_map<int,int> cnt,Max;
	scanf("%d%d",&n,&c);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		a[i]-=c;
		sum[i]=sum[i-1]+!a[i];
		cnt[a[i]]++;
		sumk[i]=cnt[a[i]];
	}
	int ans=sum[n];
	for(int i=1;i<=n;i++) Max[a[i]]=-2147483647;
	for(int i=1;i<=n;i++)
	{
		Max[a[i]]=max(Max[a[i]],sum[i-1]-sumk[i]);
		ans=max(ans,(sum[n]-sum[i]+sumk[i]+1)+Max[a[i]]);
	}
	printf("%d",ans);
	return 0;
}

1080D

Link

如果 \(n>31\)，一定有解。在大正方形中切割一次然后不断地在右下角切割即可，直接输出 Yes n-1。

如果 \(n\le 31\)，枚举路径边长 \(2^i\)（\(0\le i\le n\)），算出分割的最大次 \(\mathcal R\) 和最小次数 \(\mathcal L\)，如果 \(\mathcal L\le k\le \mathcal R\)，那么 \(i\) 即为答案。\(\mathcal L\) 很好计算，只切割路径上的正方形即可，容易推出 \(\mathcal L=\sum\limits_{j=1}^{n-i} 2^j-1\)。而 \(\mathcal R\) 比较难算，我们需要先算出将每个边长为 \(2^s\) 的正方形不断分割，使之分割成全都是 \(1\times 1\) 的正方形的次数 \(g(i)\)，有 \(g(i)=4(g-1)+1\)（\(g(0)=0\)）。有了 \(g(i)\)，就能够退出 \(\mathcal R=g(n)-(2\cdot 2^{n-i}+1)g(i)\)。可以看下面的图：

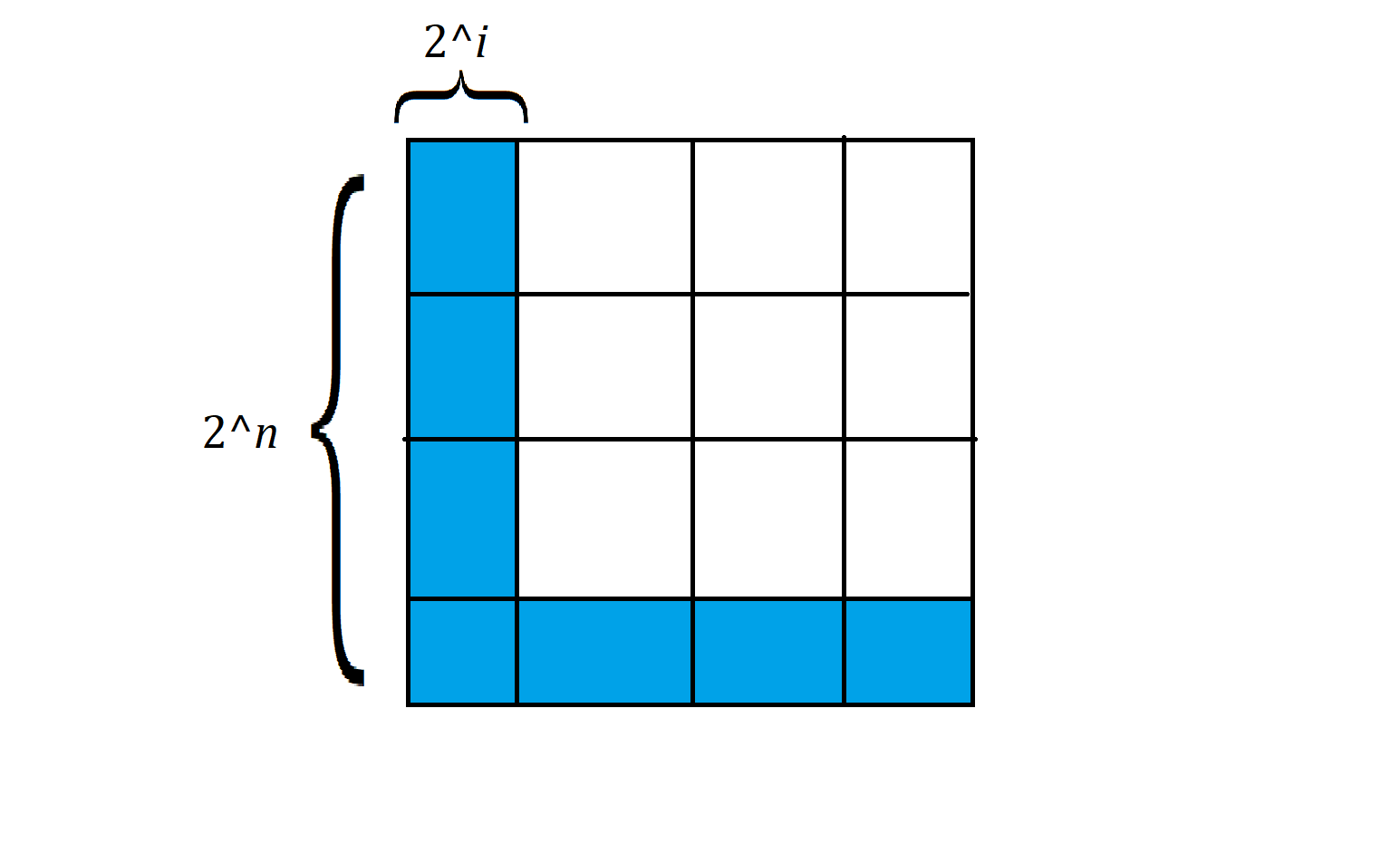
这样我们就有了一个 \(\mathcal O(n^2)\) 的做法，但实际上还能再优化。容易推出 \(\mathcal L=2^{n-i+1}-n+i-2\)，\(g(i)=(4^n-1)/3\)，通过快速幂可以将算法优化成 \(\mathcal O(Tn\log n)\)（\(1\le n\le 31\)）。

#include<bits/stdc++.h>
using namespace std;
#define int long long
int qpow(int a,int n)
{
	int ans=1;
	while(n)
	{
		if(n&1) ans*=a;
		a*=a;
		n>>=1;
	}
	return ans;
}
int n,k;
int fmin(int i) {return qpow(2,n-i+1)-n+i-2;}
int g(int i) {return (qpow(4,i)-1)/3;}
int fmax(int i) {return g(n)-(qpow(2,n-i+1)-1)*g(i);}
signed main()
{
	int T;
	cin>>T;
	while(T--)
	{
		cin>>n>>k;
		if(n>31) cout<<"YES "<<n-1<<endl;
		else
		{
			bool flag=0;
			for(int i=0;i<=n;i++)
			{
				if(fmin(i)<=k && k<=fmax(i))
				{
					flag=1;
					cout<<"YES "<<i<<endl;
					break;
				}
			}
			if(!flag) cout<<"NO"<<endl;
		}
	}
	return 0;
}

1061D

Link

考虑一种贪心：每次新来的一个区间都尽量选择最后结束的、能够与新来的区间配对的区间配对，避免浪费。如果与之前的区间匹配还不如新借一个分组或者没有能够与之配对的区间，新建一个分组。查询之前的区间可以使用 STL multiset（带重复元素的 set），可以通过 *--s.lower_bound(a[i]) 找到 multiset 中 a[i] 的前驱。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<set>
using namespace std;
#define int long long
const int N=1e5;
struct segment
{
	int l,r;
	segment(){}
}a[N+10];
bool cmp(segment x,segment y) {return x.l==y.r?x.r<y.r:x.l<y.l;}
struct node
{
	int st,ed;
	bool operator<(const node&x)const{return ed<x.ed;}
	node(int ss,int tt)
	{
		st=ss;
		ed=tt;
	}
	node(){}
};
const int MOD=1e9+7;
signed main()
{
	int n,x,y;
	scanf("%lld%lld%lld",&n,&x,&y);
	for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].l,&a[i].r);
	sort(a+1,a+n+1,cmp);
	multiset<node> s;
	int ans=0;
	s.insert(node(a[1].l,a[1].r));
	ans=x+(a[1].r-a[1].l)*y%MOD;
	for(int i=2;i<=n;i++)
	{
		multiset<node>::iterator it=s.lower_bound(node(0,a[i].l));
		if(it==s.begin())
		{
			ans+=x+(a[i].r-a[i].l)*y%MOD;ans%=MOD;
			s.insert(node(a[i].l,a[i].r));
		}
		else
		{
			node h=*--it;
			if(x+(a[i].r-a[i].l)*y<(a[i].r-h.ed)*y)
			{
				ans+=x+(a[i].r-a[i].l)*y%MOD;ans%=MOD;
				s.insert(node(a[i].l,a[i].r));
			}
			else 
			{
				ans+=(a[i].r-h.ed)*y%MOD;ans%=MOD;
				s.erase(it);
				s.insert(node(h.st,a[i].r));
			}
		}
	}
	printf("%lld",ans);
	return 0;
}

1017C

Link

注意到区间修改和区间查询，想到线段树。考虑线段树维护什么，观察到 \(1\le n,k\le 10^6,1\le m\le 2\times 10 ^5\)，显然出题人是想要让我们 \(\mathcal O(m\log m)\) 或者 \(\mathcal O(m\log n)\)。于是想到构建一棵权值线段树（因为值域是 \([1,10^6]\) 所以无需离散化），区间 \([l,r]\) 存消费在这个区间内的数量及消费总和。从 \(1\sim n\) 循环枚举时间，每次将新来的服务器及结束的服务器处理后在线段树上二分求解前 \(k\) 个的和即可。

记得开 long long。

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline void read(int &x)
{
    x=0;int f=1;
    char c=getchar();
    while(c<'0' || c>'9')
    {
        if(c=='-') f=-1;
        c=getchar();
    }
    while(c>='0' && c<='9')
    {
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    }
    x*=f;
}
const int M=2e5,N=1e6;
struct node
{
    int l,c,p,t;
    //position, count, price, type
    node(){}
    node(int pos,int cnt,int pri,int tp) {l=pos;c=cnt;p=pri;t=tp;}
    bool operator<(const node&x)const{return l<x.l;}
}a[M*4+10];
int n,k,m;
struct seg
{
    int l,r,cnt,sum;
    seg(){}
}t[N*4+10];//权值线段树
void build(int p,int l,int r)
{
    t[p].l=l;t[p].r=r;
    int mid=(l+r)/2;
    if(l==r) return;
    build(p*2,l,mid);
    build(p*2+1,mid+1,r);
}
void modify(int p,int l,int d)
{
    // printf("p:%d [%lld,%lld]\n",p,t[p].l,t[p].r);
    if(t[p].l==t[p].r)
    {
        t[p].cnt+=d;
        t[p].sum+=d*l;
        return;
    }
    int mid=(t[p].l+t[p].r)/2;
    if(l<=mid) modify(p*2,l,d);
    else modify(p*2+1,l,d);
    t[p].cnt=t[p*2].cnt+t[p*2+1].cnt;
    t[p].sum=t[p*2].sum+t[p*2+1].sum;
}
int query(int p,int k)
{
    if(t[p].l==t[p].r) return t[p].l*k;
    if(t[p*2].cnt>=k) return query(p*2,k);
    else return t[p*2].sum+query(p*2+1,k-t[p*2].cnt);
}
signed main()
{
    int n,m,k;
    scanf("%lld %lld %lld",&n,&k,&m);
    for(int i=1;i<=m;i++)
    {
        int l,r,c,p;
        scanf("%lld %lld %lld %lld",&l,&r,&c,&p);
        a[i*2-1]=node(l,c,p,1);
        a[i*2]=node(r+1,c,p,-1);
    }
    sort(a+1,a+m*2+1);
    int ans=0;
    build(1,1,1000000);
    for(int i=1,pos=1;i<=n;i++)
    {
        // printf("i=%lld, pos=%lld\n",i,pos);
        while(a[pos].l<=i && pos<=m*2)
        {
            // printf("(%lld, %lld, %lld, %lld)\n",a[pos].l,a[pos].p,a[pos].c,a[pos].t);
            modify(1,a[pos].p,a[pos].c*a[pos].t);
            pos++;
        }
        // puts("HERE");
        // printf("t[1].cnt:%lld    sum:%lld\n",t[1].cnt,t[1].sum);
        if(t[1].cnt<=k) ans+=t[1].sum;
        else ans+=query(1,k);
    }
    printf("%lld",ans);
    return 0;
}

1092E

Link

容易想到最优的图一定是个菊花图，现在我们需要考虑的就是每棵树选哪个点。一开始猜是树的重心，但是：

显然选择重心是不行的，我们选择的点应是直径的中点。为什么呢？考虑将两棵树合并成一棵树的情况，令它们的直径为别为 \(d_1,d_2\)，选的点在各自的树中能走的最远距离分别为 \(p_1,p_2\)，那么这棵树的直径就是 \(\max\{d_1,d_2,p_1+p_2+1\}\)。\(d_1\) 和 \(d_2\) 都是定值，想要让上面这个式子尽量小，只能让 \(p_1\) 和 \(p_2\) 尽量小，也就是找到树中能走的最远距离最小的点，可以发现这个点就是直径的中点。而至于重心，他的定义是「对于树上的每一个点，计算其所有子树中最大的子树节点数，这个值最小的点就是这棵树的重心」（来源：OI Wiki），子节点数量的多少并不代表着直径的长短，所以选择重心是不可行的。

找到每棵树直径的中点 \(v_i\) 后，算出所在树直径最长的点 \(v_k\)，将 \(v_k\) 与所有满足 \(j\not= k\) 的 \(j\) 连边后的直径即为最优答案。简单证（kou）明（hu）一下为什么这样做就是最优解。在新的树中，树的要么是森林中某棵树的直径，要么是某两棵树的直径取中点然后拼接起来。如果最终答案是前者，那我们无能为力，因为这是定值，无法改变；如果是后者，那我们可以让直径最大的那棵树的直径所产生的那条连保持原样，不让它有通过新连的边再增加的情况，尽量保持答案的最小。综上所述，这种做法是对的。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int N=1000,M=2000;
int head[N+10],ver[M+10],nxt[M+10],tot=0;
void add(int x,int y)
{
	ver[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
int col[N+10],cnt=0;
void dfs(int x)
{
	col[x]=cnt;
	for(int i=head[x];i;i=nxt[i])
	{
		int y=ver[i];
		if(col[y]) continue;
		dfs(y);
	}
}
vector<int> seq[N+10];//直径序列
pair<int,int> que[N+10];
int h=1,t=0,fa[N+10];
bool vis[N+10];
pair<int,int> bfs(int x,bool f)
{//first:distance, second:vertex
	memset(vis,0,sizeof(vis));
	if(f) memset(fa,-1,sizeof(fa));
	h=1;t=0;
	pair<int,int> ans=make_pair(0,0);
	que[++t]=make_pair(0,x);
	vis[x]=1;
	while(h<=t)
	{
		pair<int,int> H=que[h++];
		ans=max(ans,H);
		for(int i=head[H.second];i;i=nxt[i])
		{
			int y=ver[i];
			if(vis[y]) continue;
			vis[y]=1;
			if(f) fa[y]=H.second;
			que[++t]=make_pair(H.first+1,y);
		}
	}
	return ans;
}
int dis[N+10],v[N+10];
int main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d %d",&x,&y);
		add(x,y);
		add(y,x);
	}
	int maxx=0,f=0;
	for(int i=1;i<=n;i++)
	{
		if(!col[i])
		{
			cnt++;
			dfs(i);
			pair<int,int> tmp=bfs(bfs(i,false).second,true);
			int y=tmp.second;
			if(tmp.first>=maxx)
			{
				maxx=tmp.first;
				f=cnt;
			}
			while(~y)
			{
				seq[cnt].push_back(y);
				y=fa[y];
			}
			v[cnt]=seq[cnt][seq[cnt].size()/2];
		}
	}
	for(int i=1;i<=cnt;i++)
	{
		if(i==f) continue;
		add(v[i],v[f]);
		add(v[f],v[i]);
	}
	printf("%d\n",bfs(bfs(1,false).second,false).first);
	for(int i=1;i<=cnt;i++)
	{
		if(i==f) continue;
		printf("%d %d\n",v[i],v[f]);
	}
	return 0;
}

posted @ 2021-01-02 14:36 zzt1208 阅读(189) 评论(0) 编辑收藏举报

刷新页面返回顶部

zzt1208

SSF信息社团1月训练题目整理

Week 4（1.4 ~ 1.10）

1036C

1043E

1054D

1029D

1031D

1041E

1032D

Week 5（1.11 ~ 1.17）

1398D

1401D

1402A

1409E

1420D

1426E

1442A

Week 6（1.18 ~ 1.24）

1088D

1083B

1082E

1080D

1061D

1017C

1092E

公告