SSF信息社团12月训练题目整理
Hint:可以点击右下角的目录符号快速跳转到指定位置
Week 1(12.14 ~ 12.20)
1427C
考虑一个 \(\mathcal O(n^2)\) 的朴素 dp:令 \(f(i)\) 表示从起点到点 \(i\) 且刚好在点 \(i\) 看到明星的最优答案,则 \(f(i)=\max\limits_{1\le j<i\text{且}\operatorname{dis}(i,j)\le t_i-t_j} \{f(j)+1\}\),其中 \(\operatorname{dis}(i,j)=\vert x_i-x_j\vert+\vert y_i-y_j\vert\)。
观察题目以及不等式 \(\operatorname{dis}(i,j)\le t_i-t_j\),可以看出当 \(i-j>2r\) 时,\(j\) 一定能够到达 \(i\)(\(\operatorname{dis}(i,j)\) 最多是 \(2r\),\(\{t_i\}\) 单调递增)。也就是说,\(\max \limits_{1\le j< i-2r}\{f(j)\}\) 一定能够转移到 \(f(i)\),dp 过程中顺便存一下即可,而我们需要枚举的只有 \([i-2r+1,i-1]\) 这个区间,这样复杂度就变成了 \(\mathcal O(nr)\)。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=2e5;
int dp[N+10],t[N+10],x[N+10],y[N+10];
int main()
{
int n,r;
scanf("%d %d",&r,&n);
x[0]=y[0]=1;
for(int i=1;i<=n;i++) scanf("%d %d %d",&t[i],&x[i],&y[i]);
int mx=0xcfcfcfcf; //极小值
memset(dp,0xcf,sizeof(dp));
dp[0]=0;
for(int i=1;i<=n;i++)
{
for(int j=max(0,i-2*r+1);j<i;j++)
{
if(t[i]-t[j]>=abs(x[i]-x[j])+abs(y[i]-y[j]))
dp[i]=max(dp[i],dp[j]+1);
}
dp[i]=max(dp[i],mx+1);
if(i>=r*2) mx=max(mx,dp[i-r*2]);
}
int ans=0;
for(int j=1;j<=n;j++) ans=max(ans,dp[j]);
printf("%d",ans);
return 0;
}
1437C
将 \(\{t_i\}\) 排序,令 \(f(i,j)\) 表示前 \(i\) 个菜品在前 \(j\) 个时刻的最小代价,则容易得出 \(f(i,j)=\min\{f(i-1,j-1)+\vert j-t_i\vert,f(i,j-1)\}\),分别决策第 \(j\) 秒选或者不选菜品 \(i\)。注意 \(j\) 的循环范围是 \(1\sim 2n\) 而不是 \(1\sim n\),因为在 \(n\) 秒之后还有可能放菜品。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int N=200;
int dp[N+10][2*N+10],a[N+10];
// 选了 i 个菜品,前j秒
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+n+1);
memset(dp,0x3f,sizeof(dp));
for(int i=0;i<=2*n;i++) dp[0][i]=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=2*n;j++)
dp[i][j]=min(dp[i][j-1],dp[i-1][j-1]+abs(j-a[i]));
printf("%d\n",dp[n][n*2]);
}
return 0;
}
1437D
一个显然的性质:若 \(i>k\) 且 \(a_k>a_i\),则 \(a_k\) 不可能是 \(a_i\) 的兄弟节点(也就是说没有共同的父亲),因为题目保证遍历过程中子节点按照升序遍历。我们可以用这个性质进行贪心。
具体地,维护一个队列,将根节点插入队列,然后用类似 BFS 的方法遍历处理每一个节点。对于每一个队头 $ a_i$,我们在 $ a_i$ 后面找一个最长的子序列 \(a_{j},a_{j+1},\cdots,a_{k}(i< j\le k\le n)\),满足 \(a_j\) 是第一个未被挑选的点, \(a_{j},a_{j+1},\cdots,a_{k}\) 未被其他点挑选过且这个序列单调上升,这 \(k-j+1\) 个数就是 \(a_i\) 的子节点。类似 BFS,将这些点插入队列,然后开始下一轮求解。
容易得出这样选一定是最优的。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=2e5;
int que[N+10],h=1,t=0,d[N+10],a[N+10];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
h=1;t=0;
memset(d,0,sizeof(d));
memset(a,0,sizeof(a));
memset(que,0,sizeof(que));
int n,pos=0;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
que[++t]=1;
d[1]=0;pos=2;
int ans=0;
while(h<=t)
{
int x=que[h++];
ans=max(ans,d[x]);
int j;
for(j=pos;j<=n;j++)
if(j!=pos && a[j]<a[j-1])
break;
for(int i=pos;i<j;i++)
{
d[a[i]]=d[x]+1;
que[++t]=a[i];
}
pos=j;
}
printf("%d\n",ans);
}
return 0;
}
1444A
考虑什么情况下 \(x\) 能够满足 \(x\) 不是 \(q\) 的倍数。显然,若将他们分解成 \(\prod_{i=1}^m p_i^{c_i}\) 的质因数分解形式,则 \(x\) 的某一个 \(c_i\) 一定小于 \(q\) 的 \(c_i\),为了使 \(x\) 最大,它的 \(c_i\) 等于 \(q\) 的 \(c_i-1\),其他质因数及其指数和 \(p\) 一样。枚举这个 \(c_i\),统计哪个 \(c_i\) 能使 \(x\) 最大即可。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstring>
using namespace std;
#define int long long
int p;int q;
int qpow(int a,int n)
{
int ans=1;
while(n)
{
if(n&1) ans*=a;
a*=a;
n>>=1;
}
return ans;
}
int init()
{
int ans=0x3f3f3f3f3f3f3f3f;
for(int i=2;i*i<=q;i++)
{
if(q%i) continue;
int c1=0,c2=0;
while(q%i==0)
{
c1++;
q/=i;
}
while(p%i==0)
{
c2++;
p/=i;
}
ans=min(ans,qpow(i,c2-c1+1));
}
if(q>1)
{
int i=q;
int c1=0,c2=0;
while(q%i==0)
{
c1++;
q/=i;
}
while(p%i==0)
{
c2++;
p/=i;
}
ans=min(ans,qpow(i,c2-c1+1));
}
return ans;
}
void read(int &x)
{
x=0;int f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
x*=f;
}
void write(int x)
{
if(x<0)
{
putchar('-');
x=-x;
}
if(x>9)write(x/10);
putchar(x%10^48);
}
signed main()
{
int T;
read(T);
while(T--)
{
read(p);read(q);
if(p%q)
{
write(p);
putchar('\n');
}
else
{
write(p/init());
putchar('\n');
}
}
return 0;
}
1446B
令 \(f(i,j)\) 表示 \(A\) 的前 \(i\) 位,\(B\) 的前 \(j\) 位能够得到的最大分数,则容易得到转移方程:
注意过程中分数有可能是负数,随时和 \(0\) 取 \(\max\) 即可。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=5000;
int dp[N+10][N+10];
char s1[N+10],s2[N+10];
int main()
{
int n,m,ans=0;
scanf("%d%d%s%s",&n,&m,s1+1,s2+1);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
dp[i][j]=max(0,max(dp[i][j-1],dp[i-1][j])-1);
if(s1[i]==s2[j]) dp[i][j]=max(dp[i][j],dp[i-1][j-1]+2);
ans=max(ans,dp[i][j]);
}
printf("%d",ans);
}
1455D
Lemma:若 \(a_i>x\) 但二者不交换,则后面的数无法通过交换使序列有序。
Prove:取 \(i<j\le n\),假设 \(a_i,a_j\) 都能与 \(x\) 交换,即 \(a_i>x,a_j>x\)。
若 \(a_i\) 不交换但 \(a_j\) 交换,则交换后的 \(a_j'=x<a_i\),这与题目要求的单调不降不符,而且这两个数无法再次还原,所以 \(a_i\) 与 \(x\) 必须交换。
\(\mathcal{Q.E.D.}\)
由 Lemma,我们可以扫一遍序列,对于每个 \(a_i\),一旦可以与 \(x\) 交换就执行操作同时累加次数,若执行过程中序列已经有序,输出答案并直接退出;若序列已经扫描完毕但仍然不是有序的,说明无解,输出 -1。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=500;
int a[N+10],n;
bool check()
{
for(int i=2;i<=n;i++)
if(a[i]<a[i-1])
return false;
return true;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int x;
scanf("%d %d",&n,&x);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
if(check())
{
printf("0\n");
continue;
}
int ans=0;
for(int i=1;i<=n;i++)
{
if(a[i]>x)
{
swap(a[i],x);
ans++;
}
if(check())
{
printf("%d\n",ans);
break;
}
}
if(!check()) printf("-1\n");
}
return 0;
}
Week 2(12.21 ~ 12.27)
1462F
枚举哪个线段与其他所有线段重合,并通过树状数组计算与之重合的线段的数量,数量最多的即为所求线段。
至于如何统计,可以将所有线段以左端点为第一关键字、右端点为第二关键字排序,对于每一个线段 \([l_i,r_i]\),左端点小于它的(\([l_1,r_1],[l_2,r_2],\cdots,[l_{i-1},r_{i-1}]\)),统计右端点处于区间 \([l_i,+\infty)\) 的有多少个;左端点大于它的(\([l_{i+1},r_{i+1}],[l_{i+2},r_{i+2}],\cdots,[l_n,r_n]\)),统计左端点处于区间 \([l_i,r_i]\),二者相加的和即与该线段重合的线段的数量。由于 \(1 \leq l \leq r \leq 10^9\),树状数组统计前需要离散化。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int N=2e5;
struct segment
{
int l,r;
segment() {}
bool operator < (const segment &x) const {return l==x.l?r<x.r:l<x.l;}
}a[N+10];
int c1[N*2+10],c2[N*2+10],n,m,t[N*2+10];
void modify(int *c,int x,int d) {for(;x<=m;x+=x&-x) c[x]+=d;}
int query(int *c,int x)
{
int ans=0;
for(;x;x-=x&-x) ans+=c[x];
return ans;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d %d",&a[i].l,&a[i].r);
t[i*2-1]=a[i].l;
t[i*2]=a[i].r;
}
sort(a+1,a+n+1);
sort(t+1,t+n*2+1);
m=unique(t+1,t+n*2+1)-t-1;
for(int i=0;i<=m;i++)
{
c1[i]=0;
c2[i]=0;
}
for(int i=1;i<=n;i++)
{
a[i].l=lower_bound(t+1,t+m+1,a[i].l)-t;
a[i].r=lower_bound(t+1,t+m+1,a[i].r)-t;
}
int ans=0;
for(int i=1;i<=n;i++) modify(c2,a[i].l,1);
for(int i=1;i<=n;i++)
{
ans=max(ans,query(c1,m)-query(c1,a[i].l-1)+query(c2,a[i].r)-query(c2,a[i].l-1));
modify(c2,a[i].l,-1);
modify(c1,a[i].r,1);
}
printf("%d\n",n-ans);
}
return 0;
}
1442B
拿到题没有思路,然后大力猜结论,本来以为 WA On Test 2,结果改一个取模就 AC 了,RP 真好((
观察到如果想把某个数 \(a_i\) 加入 \(b\),则一定要在 \(a_{i-1}\) 和 \(a_{i+1}\) 中删掉一个。在纸上画画后我们发现一个规律:
令 \(p_i\) 表示 \(b_i\) 在 \(\{a_i\}\) 中的下标,\(t_i\) 表示 $ a_i$ 在 \(\{b_i\}\) 中的下标(如果 \(a_i\notin \{b_i\}\) 则令 \(t_i=0\))。
枚举 \(b_i\),令当前 \(b_i\) 对答案的贡献 \(c_i=0\),若 \(p_i>1\) 且 \(t_{p_i-1}<t_{p_i}\),\(c_i\) 加一;类似地,若 \(p_i<n\) 且 \(t_{p_i+1}<t_{p_i}\),\(c_i\) 加一。
\(\prod_{i=1}^m c_i\) 即为所求。
大白话版本:每个 \(a_i\) 都找到自己在 \(\{b_i\}\) 中是第几个被“提到”的(就是 \(t_i\)),如果左边的数没被提及过或者说左边的数比他提及的早,\(c_i\gets c_i+1\)(即 c[i]++);右边做同样的操作,最后把 \(c_i\) 乘起来就是答案。如果还无法理解可以直接翻下面的代码。
接下来证明一下为什么这样做是对的。
仔细思考一下,对于这个做法我们的迷惑点实际上是这样的:如果旁边的数已经前面的数删了,并且比当前这个数晚提及,那么答案就是错的。但实际上,这个命题是不存在的。以右边为例,如果发生这种情况,删除过程中一定会有一个情形:
若 $ a_i$ 为当前正在计算的数,则此时 \(t_{i}>t_{i+1}<t_{i+2}\)。
对于这种情况,根据前面的算法,\(c_{i+1}=0\)。因为计算总贡献时是 \(\prod\) 而不是 \(\sum\),所以如果出现这种情况答案肯定是 \(0\),就算 \(c_i\) 计算错了也无伤大雅;如果最后的答案不是 \(0\),就肯定不会出现这种情况。
\(\mathcal{Q.E.D.}\)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int N=2e5;
int a[N+10],b[N+10],tg[N+10],pos[N+10];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
memset(tg,-1,sizeof(tg));
int n,m;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
pos[a[i]]=i;
}
for(int i=1;i<=m;i++)
{
scanf("%d",&b[i]);
tg[pos[b[i]]]=i;
}
int ans=1;
for(int i=1;i<=m;i++)
{
int cnt=0;
if(pos[b[i]]>1 && tg[pos[b[i]]-1]<tg[pos[b[i]]]) cnt++;
if(pos[b[i]]<n && tg[pos[b[i]]+1]<tg[pos[b[i]]]) cnt++;
ans*=cnt;
ans%=998244353;
}
printf("%d\n",ans);
}
return 0;
}
1462E2
首先我们注意到 tag 里面有一个 sorting,将 \(\{a_i\}\) 排序,这时对于一个方案 \(i_1<i_2<i_3<\cdots<i_m\) 一定满足 \(a_{i_1}<a_{i_2}<a_{i_3}<\cdots<a_{i_m}\)。我们可以枚举 \(i_1\),同时二分能够满足 \(a_j-a_{i_1}\le k\) 的最大的 \(j\),在 \([i_1,j]\) 中挑选 \(k\) 个数即可,这个区间的方案数即为组合数 \(\mathrm C_{j-i_1}^{m-1}\)(为什么不是 \(\mathrm C_{j-i_1+1}^m\)?因为 \(a_{i_1}\) 必须选)。
因为此题需要取模,所以需要预处理出 \(1\sim n\) 的阶乘(取模之后的结果)和它们的逆元,根据公式 \(\mathrm C_n^m=\dfrac{n!}{(n-m)!m!}\) 求解。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
#define int long long
const int N=2e5,MOD=1e9+7;
int p[N+10],inv[N+10],a[N+10];
int qpow(int a,int n)
{
int ans=1;a%=MOD;
while(n)
{
if(n&1) ans=ans*a%MOD;
a=a*a%MOD;
n>>=1;
}
return ans;
}
void init()
{
p[0]=1;
inv[0]=1;
for(int i=1;i<=N;i++)
{
p[i]=p[i-1]*i%MOD;
inv[i]=qpow(p[i],MOD-2);
}
}
signed main()
{
init();
int T;
scanf("%lld",&T);
while(T--)
{
int n,m,k;
scanf("%lld %lld %lld",&n,&m,&k);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
sort(a+1,a+n+1);
int ans=0;
for(int i=1;i<=n;i++)
{
int l=1,r=n,pos=0;
while(l<=r)
{
int mid=(l+r)/2;
if(a[mid]<=a[i]+k)
{
l=mid+1;
pos=mid;
}
else r=mid-1;
}
//C_{pos-i}^{m-1}
int mm=m-1,nn=pos-i;
if(mm>nn) continue;
ans=(ans+p[nn]*inv[mm]%MOD*inv[nn-mm]%MOD)%MOD;
}
printf("%lld\n",ans);
}
}
1453C
分别从上到下、从左到右扫一遍。二者核心思路一样,所以只讲从上到下扫。
对于每个数字 \(d\) 统计它出现的最高位置(即对于所有 \(a_{x,y}=d\),统计出最小的 \(x\)) \(x_1\) 和最低位置 \(x_2\),显然,此时 \(\mathrm{ans}_d=\max\limits_{1\le i,j\le n} \{\max\{j-1,n-j\}\times\max\{i-x_1,x_2-i\}\}\)。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int N=2000,INF=0x7fffffff;
char a[N+10][N+10];int Min[10],Max[10],cnt[10],ans[10];
void read(int &x)
{
x=0;int f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
x*=f;
}
int main()
{
int T;read(T);
while(T--)
{
int n;read(n);
for(int i=0;i<10;i++)
{
Min[i]=n+1;
Max[i]=0;
cnt[i]=0;
ans[i]=0;
}
for(int i=1;i<=n;i++) scanf("%s",a[i]+1);
for(int i=1;i<=n;i++) //row
{
for(int j=1;j<=n;j++)
{
cnt[a[i][j]^48]++;
Min[a[i][j]^48]=min(Min[a[i][j]^48],i);
Max[a[i][j]^48]=max(Max[a[i][j]^48],i);
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(cnt[a[i][j]^48]<=1) continue;
ans[a[i][j]^48]=max(ans[a[i][j]^48],max(j-1,n-j)*max(i-Min[a[i][j]^48],Max[a[i][j]^48]-i));
}
}
for(int i=0;i<10;i++)
{
Min[i]=n+1;
Max[i]=0;
}
for(int i=1;i<=n;i++) //column
{
for(int j=1;j<=n;j++)
{
Min[a[i][j]^48]=min(Min[a[i][j]^48],j);
Max[a[i][j]^48]=max(Max[a[i][j]^48],j);
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(cnt[a[i][j]^48]<=1) continue;
ans[a[i][j]^48]=max(ans[a[i][j]^48],max(i-1,n-i)*max(j-Min[a[i][j]^48],Max[a[i][j]^48]-j));
}
}
for(int i=0;i<10;i++) printf("%d ",ans[i]);
printf("\n");
}
return 0;
}
1451D
必胜策略:将棋子不断地调整到 \(y=x\) 的直线上(yh, yyds),即若前面的人将 \(x\) 增加 \(k\),此轮就将 \(y\) 增加 \(k\);若前面的人将 \(y\) 增加 \(k\),此轮就将 \(x\) 增加 \(k\)。统计这种情况能持续多少轮,若为奇数,先手胜;反之,后手胜。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int d,k;
scanf("%d %d",&d,&k);
int x=0,y=0,pos=0,ans=0;
while(1)
{
if(pos) x+=k;
else y+=k;
pos^=1;
if((long long)x*(long long)x+(long long)y*(long long)y>(long long)d*(long long)d) break;
ans++;
}//sqrt(x*x+y*y)<=d
//=> x*x+y*y<=d*d
printf(ans%2?"Ashish\n":"Utkarsh\n");
}
return 0;
}
1450D
对于 \(k=1\) 和 \(k=n\),特判即可。
对于 \(k\in[2,n-1]\),首先注意到 \(1\) 必须在边界并且有且只能有一个,否则就会被包括两次;,把 \(1\) 去掉,\(2\) 也只能在边界并且有且只能有一个;\(3,4,\cdots n-k+1\) 同理。注意到如果 \(k\) 满足条件,那么 \(k+1\) 一定满足条件,因为限制只是更宽了。所以从大到小枚举 \(k\),直到不符合条件就退出,这时的 \(k\) 就是符合条件的最小的 \(k\),\(\forall i<k,\mathrm{ans}_i=0\);\(\forall i \ge k,\mathrm{ans}_i=1\)。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<deque>
using namespace std;
const int N=3e5;
int a[N+10],cnt[N+10];bool ans[N+10];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++) cnt[i]=ans[i]=0;
bool flag=1; // k = n
int minn=0x7fffffff; // k = 1
deque<int> que;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
que.push_back(a[i]);
if(cnt[a[i]]) flag=0;
cnt[a[i]]++;
minn=min(minn,a[i]);
}
for(int i=1;i<=n;i++) // yh, yyds
{
int k=n-i+1;
if(!cnt[i]) break; // 如果序列中没有 k,则不可能构造出合法的排列
cnt[i]--;
ans[k]=1;
/*
一个问题:为什么下面几个break不放在前面?如果下面几个break成立不是说明这个序列不合法吗?
实际上并不是的。从样例一就可以看出,当k=3时,que[l]!=k,que[r]!=k,但实际上k=3的时候还是成立的。
考虑为什么我们要判断a[l,r]!=k,这个判断其实判断的并不是k的情况,而是k-1的情况。
k的情况会包含整个序列,所以只要k在这个序列中出现即可,不需要考虑position;
而k-1的情况,会被长度为k-1的两个区间包括,这个时候才是不符合条件的。
*/
if(cnt[i]) break;
if(que.front()==i) que.pop_front();
else if(que.back()==i) que.pop_back();
else break;
}
ans[1]=flag;
ans[n]=minn==1;
for(int i=1;i<=n;i++) putchar(48^ans[i]);
putchar('\n');
}
return 0;
}
Week 3(12.28 ~ 1.3)
963B
为表述方便,将节点数为偶数的子树称为 Even 树,反之称之为 Odd 树。(借鉴这篇博客)
首先当这棵树为 Even 树时,答案一定是 NO,因为若节点数量为偶数则边的数量为奇数,而每次只能删除偶数条边,最终会剩下一条边无论如何也无法删除。
反之,则答案一定是 YES。我们可以按照 Even 子树 → 根 → Odd 子树的顺序构造删除方法,即递归 Even 子树完毕后删除根,随后递归 Odd 子树。证明如下。
Lemma1:一颗 Odd 树的子树一定能分为根、若干个 Even 树和偶数个 Odd 树。
Lemma2:一颗 Even 树的子树一定能分为根、若干个 Even 树和奇数个 Odd 树。
这两个 Lemma 的证明显然。
假设我们当前递归到的节点是 \(x\),若 \(x\) 是一颗 Odd 树,由 Lemma1,将所有 Even 子树删除后 \(x\) 还剩余偶数条边,此时可以删除 \(x\),继续递归 Odd 子树;若 \(x\) 是一颗 Even 树,由 Lemma2,将所有 Even 树删除后 \(x\) 与后代有奇数条边,与父亲还有一条边,加起来是偶数条边,仍然可以将 \(x\) 删除。最后,Odd 树与 Even 树一定都会收敛到下面的情况:
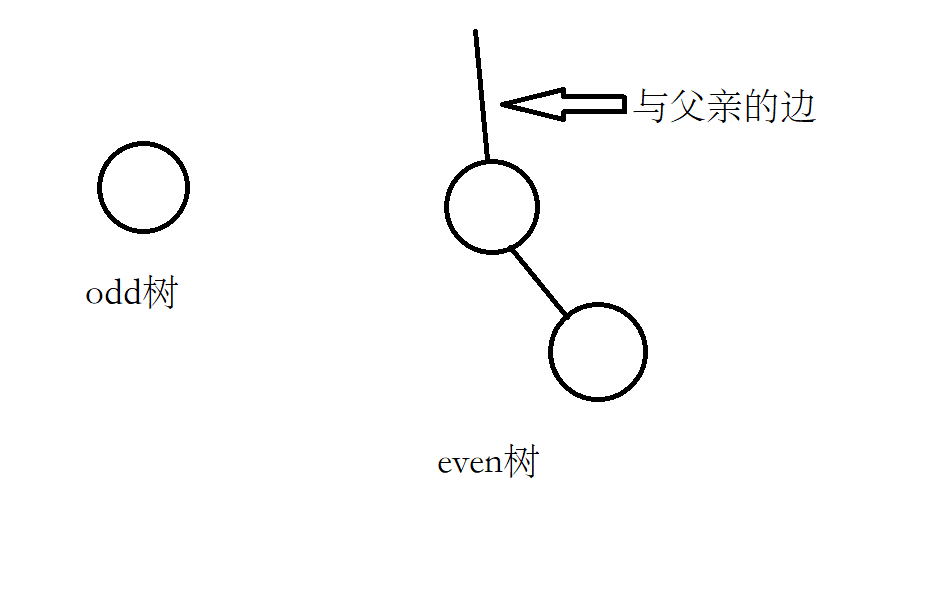
这两种情况都可以删除。
\(\mathcal{Q.E.D.}\)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<vector>
using namespace std;
const int N=2e5,M=4e5;
int head[N+10],ver[M+10],nxt[M+10],tot,sz[N+10];//d[]:degree
void add(int x,int y)
{
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
ver[++tot]=x;
nxt[tot]=head[y];
head[y]=tot;
}
void dfs1(int x,int fa)//init sz
{
sz[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
if(y==fa) continue;
dfs1(y,x);
sz[x]+=sz[y];
}
}
int ans[N+10],cnt=0;
void dfs2(int x,int fa)//delete
{
vector<int> odd,even;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
if(y==fa) continue;
// printf("(%d -> %d)\n",x,y);
if(sz[y]&1) odd.push_back(y);
else even.push_back(y);
}
//even -> 根 -> odd
for(int i=0;i<even.size();i++)
{
int y=even[i];
dfs2(y,x);
}
ans[++cnt]=x;
for(int i=0;i<odd.size();i++)
{
int y=odd[i];
dfs2(y,x);
}
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
if(!x) continue;
add(i,x);
}
dfs1(1,-1);
if(!(sz[1]&1)) printf("NO");
else
{
printf("YES\n");
dfs2(1,-1);
for(int i=1;i<=cnt;i++) printf("%d\n",ans[i]);
}
return 0;
}
965C
从 \(1\) 到 \(D\) 枚举共进行了几轮,显然当前这一轮第只分到一号能使一号拿到的糖最多,此时 \(x=\lfloor \dfrac{n}{(d-1)k+1}\rfloor\)。但这时有可能 \(x>M\),令 \(x=M\) 即可。
但是这样会爆 long long,有两种解决方法:
- 用 Python 写
- 注意到当 \(\lfloor \dfrac{n}{(d-1)k+1}\rfloor=0\) 的时候肯定无法得到最优解,于是随时特判,若出现这种情况则直接
break掉。
C++:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
int main()
{
ll n,k,M;ll D;
scanf("%lld%lld%lld%lld",&n,&k,&M,&D);
ll ans=0;
for(int d=0;d<=D;d++)
{
ll x=n/((d-1)*k+1);
if(x==0) break;
if(x>M) x=M;
ans=max(ans,x*d);
}
printf("%lld",ans);
return 0;
}
Python:
s=list(map(int,input().split()))
n=s[0]
k=s[1]
M=s[2]
D=s[3]
ans=0
for d in range(0,D+1):
x=n//((d-1)*k+1)
if x>M:
x=M
if x*d>ans:
ans=x*d
print(ans)
975D
字丑勿喷/kel

注:因为分式分母不能为 \(0\),所以统计答案时不仅要保证 \(kV_{x_1}-V_{y_1}=kV_{x_2}-V_{y_2}\),也要保证 \(V_{x_1}\not=V_{x_2}\) 且 \(V_{y_1}\not=V_{y_2}\)。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
using namespace std;
#define int long long
const int N=2e5,MOD=1e6+7;
struct Hash
{
int head[MOD+10],val[N+10],nxt[N+10],cnt[N+10],tot;
Hash()
{
memset(cnt,0,sizeof(cnt));
memset(head,0,sizeof(head));
tot=0;
}
void ins(int x)
{
int key=(x%MOD+MOD)%MOD;
for(int i=head[key];i;i=nxt[i])
{
if(val[i]==x)
{
cnt[i]++;
return;
}
}
val[++tot]=x;
nxt[tot]=head[key];
head[key]=tot;
cnt[tot]=1;
}
int query(int x)
{
int key=(x%MOD+MOD)%MOD;
for(int i=head[key];i;i=nxt[i])
if(val[i]==x)
return cnt[i];
return 0;
}
}ha/*,hb*/;
map<pair<int,int>,int> vis;//向STL低头
signed main()
{
int n,k,b;
scanf("%lld %lld %lld",&n,&k,&b);
int ans=0;
for(int i=1;i<=n;i++)
{
int x,vx,vy;
scanf("%lld %lld %lld",&x,&vx,&vy);
ans+=ha.query(k*vx-vy)-vis[make_pair(vx,vy)];
ha.ins(k*vx-vy);
vis[make_pair(vx,vy)]++;
//hb.ins(vx);
}
printf("%lld",ans*2);
return 0;
}
997B
很容易写出一个 \(\mathcal O(n^3\log n)\) 的暴力:(\(\log\) 是 map 的复杂度)
#include<bits/stdc++.h>
using namespace std;
int main()
{
map<long long,bool> vis;
long long n,ans=0;
scanf("%lld",&n);
for(int i=0;i<=n;i++)
{
for(int v=0;v<=n-i;v++)
{
for(int x=0;x<=n-i-v;x++)
{
int l=n-i-v-x;
long long X=i+v*5ll+x*10ll+l*50ll;
if(!vis[X]) ans++;
vis[X]=1;
}
}
}
printf("%lld",ans);
return 0;
}
观察到这题的数据范围 \(1\le n\le 10^{18}\),猜测这题是一个结论题,于是打表找规律:
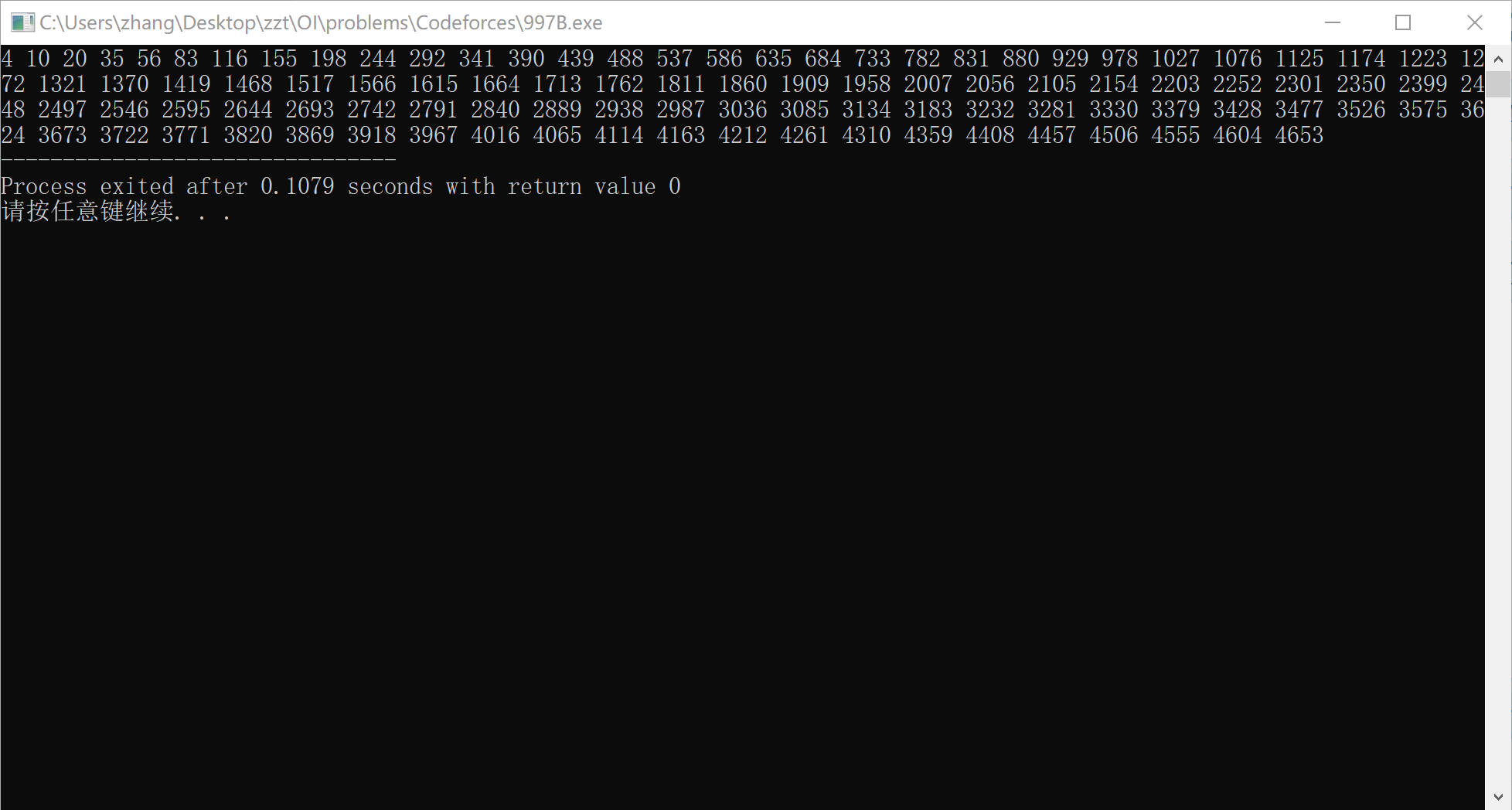
发现当 \(n\ge 12\) 的时候答案是一个公差为 \(49\) 的等差数列,于是就可以 \(\mathcal O(1)\) 求了。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int ans[12]={0,4,10,20,35,56,83,116,155,198,244,292};
int main()
{
int n;
scanf("%d",&n);
if(n<=11) printf("%d",ans[n]);
else printf("%lld ",292ll+(n-11)*49ll);
return 0;
}
999E
注意到两个关键信息:有向图(The roads in Berland are one-way),连通性(reachability),想到强连通分量,于是我们有了这样一个做法:将原图 \(G\) 通过强连通分量缩点为 \(G'\),显然 \(G'\) 是一个有向无环图,统计 \(G'\) 中入度为 \(0\) 的点的数量即可(源点 \(s\) 所在的强连通分量不计)。
简单证明一下:在 \(G'\) 中,一个入度不为 \(0\) 的点必定有若干个点能通过一条边直接到达它,这些点中有入度为 \(0\) 的,有入度不为 \(0\) 的,对于入度为 \(0\) 的点,用这个方法继续向上追溯,由于有向无环图不存在一个独立子图使得这张图内所有点的入度都不为 \(0\),所以最终追溯到的点一定都是入度为 \(0\) 的。将这些入度为 \(0\) 的点与 \(s\) 连一条边就能使得整个图 \(G'\) 都能到达 \(s\)。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
inline void read(int &x)
{
x=0; int f=1;
char c=getchar();
while(c<'0' || c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0' && c<='9')
{
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
x*=f;
}
const int N=5000,M=5000;
int head[N+10],ver[M+10],nxt[M+10],tot=0;
inline void add(int x,int y)
{
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
int dfn[N+10],low[N+10],st[N+10],top=0,num=0,col[N+10],cnt=0;
bool vis[N+10];
void tarjan(int x)
{
low[x]=dfn[x]=++num;
st[++top]=x;
vis[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int y=ver[i];
if(!dfn[y])
{
tarjan(y);
low[x]=min(low[x],low[y]);
}else if(vis[y]) low[x]=min(low[x],dfn[y]);
}
if(low[x]==dfn[x])
{
int y=0;cnt++;
do
{
y=st[top--];
vis[y]=0;
col[y]=cnt;
}while(x!=y);
}
}
int in[N+10];
int main()
{
int n,m,s;
scanf("%d %d %d",&n,&m,&s);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d %d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
// for(int i=1;i<=n;i++) printf("%d ",col[i]);
for(int i=1;i<=n;i++)
for(int j=head[i];j;j=nxt[j])
if(col[i]!=col[ver[j]])
in[col[ver[j]]]++;
int ans=0;
for(int i=1;i<=cnt;i++) if(!in[i]) ans++;
if(!in[col[s]]) ans--;
printf("%d",ans);
return 0;
}
999F
首先注意到 \(\{c_i\}\) 中所有无人喜欢的数字都是无用的,将 \(\{f_i\}\) 去重,对于每个 \(f_i\),统计数字数量 \(n\) 和喜欢这个数字的人数 \(m\),问题就成为了 \(n\) 个人分 \(m\) 张卡,每个人最多 \(k\) 张,卡片数量对应一个分值 \(h_i\),求最大得分。令 \(\operatorname{dp}(i,j)\) 表示前 \(i\) 个人分前 \(j\) 张卡得到的最大分值,容易得到 \(\operatorname{dp}(i,j)=\max\limits_{l=0}^{\min\{j,k\}}\{\operatorname{dp}(i-1,j-l)+h_l\}\)。将所有 \(f_i\) 的 \(\operatorname{dp}(n,m)\) 累加即可。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
const int N=500,K=10,VAL=1e5;
long long dp[N+10][N*K+10];
int h[K+10],f[N+10];
int card[VAL+10],cnt[VAL+10]; //卡片数量 人数
int main()
{
int n,k;
scanf("%d%d",&n,&k);
for(int i=1;i<=n*k;i++)
{
int x;
scanf("%d",&x);
card[x]++;
}
for(int i=1;i<=n;i++)
{
scanf("%d",&f[i]);
cnt[f[i]]++;
}
sort(f+1,f+n+1);n=unique(f+1,f+n+1)-f-1;
for(int i=1;i<=k;i++) scanf("%d",&h[i]);
long long ans=0;
for(int col=1;col<=n;col++)
{
int nn=cnt[f[col]],mm=card[f[col]];
memset(dp,0,sizeof(dp));
for(int i=1;i<=nn;i++)
for(int j=1;j<=mm;j++)
for(int l=0;l<=min(j,k);l++)
dp[i][j]=max(dp[i][j],dp[i-1][j-l]+h[l]);
ans+=dp[nn][mm];
}
printf("%lld",ans);
return 0;
}
1142B
我们定义 \(a_i\)(\(1\le i\le m\)) 的下一个位置为:在排列中找到一个数 \(p_j\) 使得 \(p_j=a_i\),若 \(j\in[1,n-1]\),则 \(a_i\) 的下一个位置为满足 \(a_k=p_{j+1}\) 且 \(k>i\) 的最小的 \(k\),若 \(\forall k\in[i+1,n],a_k\not= p_{j+1}\),令 \(a_i\) 的下一个位置为 \(+\infty\);若 \(j=n\),则 \(a_i\) 的下一个位置为满足 \(a_k=p_1\) 且 \(k>i\) 的最小的 \(k\),若 \(\forall k\in[i+1,n],a_k\not= p_1\),令 \(a_i\) 的下一个位置为 \(+\infty\)。\(a_i\) 的下 \(n\) 个位置定义为 \(a_i\) 的下一个位置的下一个位置的下一个位置……的下一个位置(重复 \(n\) 遍),若没有,记作 \(+\infty\)。
定义 \(f(i,j)\) 表示 \(a_i\) 的下 \(2^j\) 个位置,则显然有 \(f(i,j)=f(f(i,j-1),j-1)\),预处理出所有的 \(f(i,j)\) 需要 \(\mathcal O(m\log m)\) 的时间。有了 \(f(i,j)\),就可以对任意的 \(i\) 和 \(j\) 在 \(\mathcal O(\log j)\) 的时间内回答 \(i\) 的下 \(j\) 个位置(对 \(j\) 二进制拆分),为了方便叙述,将其记为 \(g(i,j)\)。
通过上面这些定义,我们发现题目中对区间 \([l_i,r_i]\) 的查询,实际上就是在询问 \(\min\limits_{i=l_i}^{r_i} \{g(i,n-1)\}\) 是否 \(\le r_i\),使用线段树或 ST 表回答即可。
时间复杂度 \(\mathcal O((m+q) \log m)\)。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=2e5;
int p[N+10],a[N+10],pos[N+10];
struct seg {int l,r,min;} t[N*4+10];
int nxt[N+10][20];
int get(int x,int n)
{
int ans=x,cnt=0;
while(n)
{
if(n&1) ans=nxt[ans][cnt];
if(ans>=0x7f7f7f7f) break;
n>>=1;cnt++;
}
return ans;
}
int n;
void build(int p,int l,int r)
{
t[p].l=l;t[p].r=r;
if(l==r)
{
t[p].min=get(l,n-1);
return;
}
int mid=(l+r)/2;
build(p*2,l,mid);
build(p*2+1,mid+1,r);
t[p].min=min(t[p*2].min,t[p*2+1].min);
}
int query(int p,int l,int r)
{
if(l<=t[p].l && t[p].r<=r) return t[p].min;
int mid=(t[p].l+t[p].r)/2,ans=0x7f7f7f7f;
if(l<=mid) ans=min(ans,query(p*2,l,r));
if(r>mid) ans=min(ans,query(p*2+1,l,r));
return ans;
}
int ans[N+10];
int main()
{
int m,q;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
{
scanf("%d",&p[i]);
pos[p[i]]=i;
}
for(int i=1;i<=m;i++)
{
scanf("%d",&a[i]);
a[i]=pos[a[i]];
}
memset(pos,0x7f,sizeof(pos));
for(int i=m;i;i--)
{
nxt[i][0]=pos[a[i]==n?1:a[i]+1];
pos[a[i]]=i;
}
int logn=(int)(log(n)/log(2))+1;
for(int s=1;s<=logn;s++)
{
for(int i=1;i<=m;i++)
{
if(i+(1<<s)-1>m)
{
nxt[i][s]=0x7f7f7f7f;
continue;
}
if(nxt[i][s-1]>m)
{
nxt[i][s]=0x7f7f7f7f;
continue;
}
nxt[i][s]=nxt[nxt[i][s-1]][s-1];
}
}
build(1,1,m);
for(int i=1;i<=q;i++)
{
int l,r;
scanf("%d%d",&l,&r);
int tmp=query(1,l,r);
ans[i]=(tmp<=r);
}
for(int i=1;i<=q;i++) putchar(48^ans[i]);
return 0;
}

