LOJ#2452. 「POI2010」反对称 Antisymmetry
48分做法
枚举每个子串,用 hash 逐一判断是否为反对称字符串。
时间复杂度为 \(\mathcal O(n^2)\),而此题 \(n\le 5\times 10^5\),只能得到 \(48\) 分。
100分做法
观察到 \(n\) 的数据范围,可知此题的复杂度要在 \(\mathcal O(n\log n)\) 及以下。于是,不难想到二分。
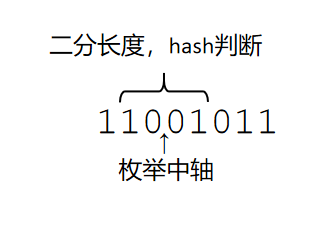
不难得出,每个反对称字符串的长度一定是偶数,这样我们就可以枚举每个字符串中间的空隙(中轴),然后二分配合 hash 求中轴为 \(l\) 的最长反对称字符串长度 \(l\),每次 \(\mathrm{ans}\) 加上 \(l/2\) 就是最终答案。这是因为,如果一个串 \(s\) 为反对称字符串,那么 \(s\) 所有以 \(l\) 为中轴的子串都是反对称字符串,这样的子串共 \(l/2\) 个。可以自己模拟一下试试。实际实现中,二分的是 \(l/2\),这样更方便一些。
可以配合图理解一下:
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=5e5,base=1e9+7;
char s[N+10];
ull h1[N+10],h2[N+10],p[N+10];
bool t1[N+10],t2[N+10];
int n;
void init()
{
p[0]=1ull;
for(int i=1;i<=n;i++) p[i]=p[i-1]*base;
for(int i=1;i<=n;i++) h1[i]=h1[i-1]*base+(s[i]=='1');
for(int i=1;i<=n;i++) h2[i]=h2[i-1]*base+(s[n-i+1]=='0');
}
ull hs(ull *h,int l,int r) {return h[r]-h[l-1]*p[r-l+1];}
bool check(int l,int r) {return hs(h1,l,r)==hs(h2,n-r+1,n-l+1);}
int erfen(int i)
{
int l=0,r=min(i,n-i),ans=0;
while(l<=r)
{
int mid=(l+r)/2;
if(check(i-mid+1,i+mid))
{
l=mid+1;
ans=mid;
}
else r=mid-1;
}
return ans;
}
int main()
{
ll ans=0;
scanf("%d%s",&n,s+1);
init();
for(int i=1;i<n;i++) ans+=erfen(i);
printf("%lld",ans);
return 0;
}
据说马拉车 Manacher 也能做?但我不会。。


