SPFA算法

转载自https://blog.csdn.net/weixin_43902449/article/details/88605417（代码部分除外）

---

一.算法简介

SPFA（Shortest Path Faster Algorithm）算法是求单源最短路径的一种算法，它是 Bellman-Ford 的队列优化，它是一种十分高效的最短路算法。外号斯（S）普（P）发（FA）。

很多时候，给定的图存在负权边，这时类似 Dijkstra 等算法便没有了用武之地，而 Bellman-Ford 算法的复杂度又过高，SPFA 算法便派上用场了。

在段凡丁的论文中，SPFA 的复杂度是 \(\mathcal O(km)\)，其中 \(k\) 是一个常数。但后来被人指出复杂度证明有错误，最坏情况下还是会退化到 \(\mathcal O(nm)\)。NOI2018 D1T1 的出题人卡掉了 SPFA，于是就有了这个梗：

不过 SPFA 还是要学的。

接下来讲一下算法流程。建立一个队列，初始时队列里只有起始点，在建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为 \(0\)）。然后执行松弛操作，用队列里有的点去刷新起始点到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。

此外，SPFA 算法还可以判断图中是否有负权环，即一个点入队次数超过 \(n\)。

---

二.算法图解

给定一个有向图，求 \(A\to E\) 的最短路。

源点 \(A\) 首先入队，并且 \(A\to B\) 松弛。

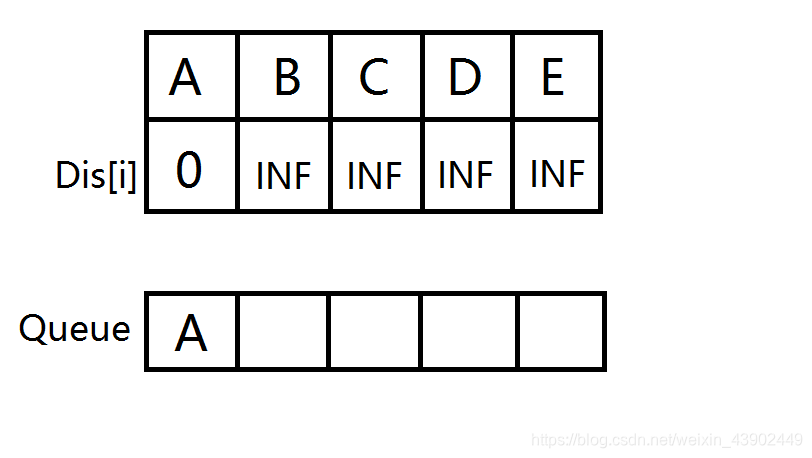
扩展与 \(A\) 相连的边，\(B,C\) 入队并松弛。

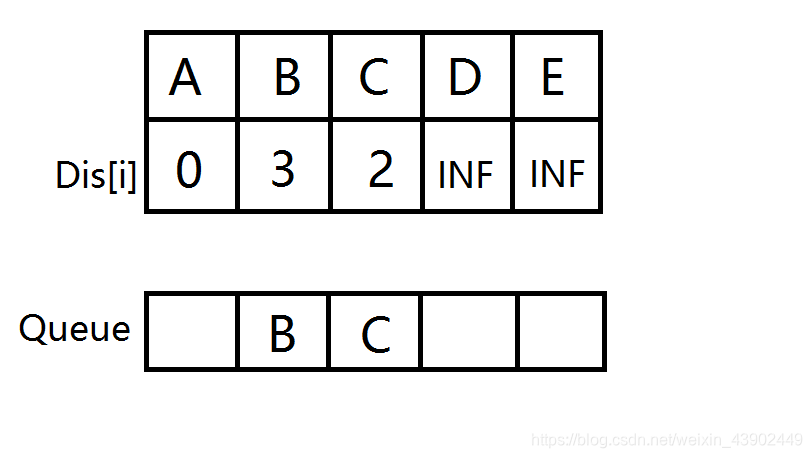
\(B,C\) 分别开始扩展，\(D\) 入队并松弛。

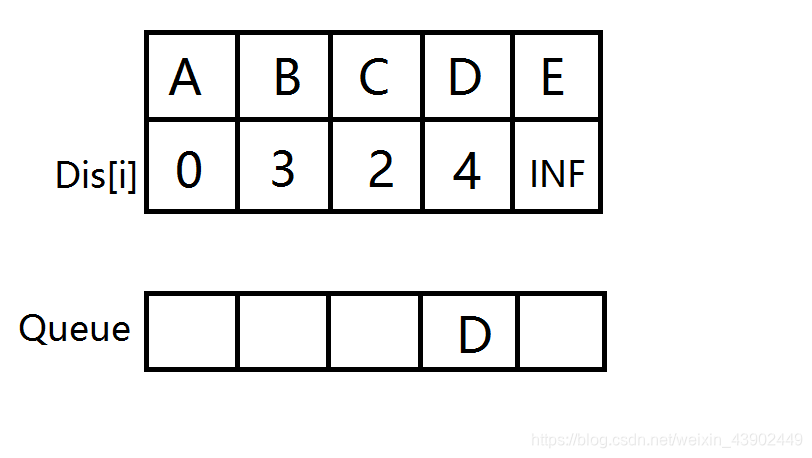
\(D\) 出队，\(E\) 入队并松弛。

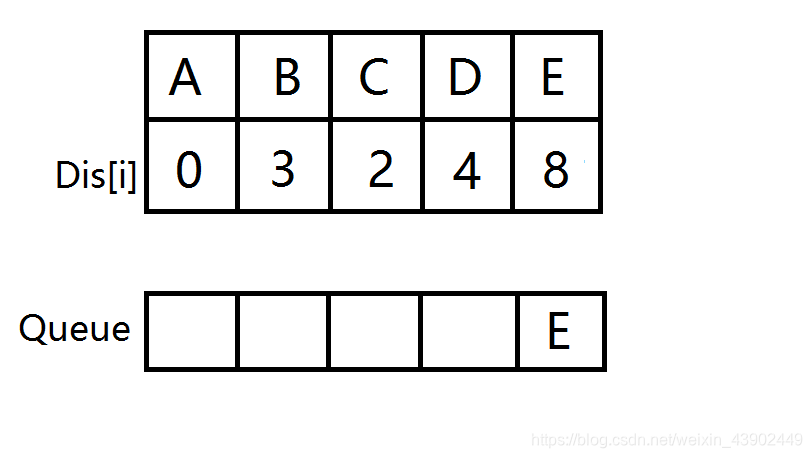
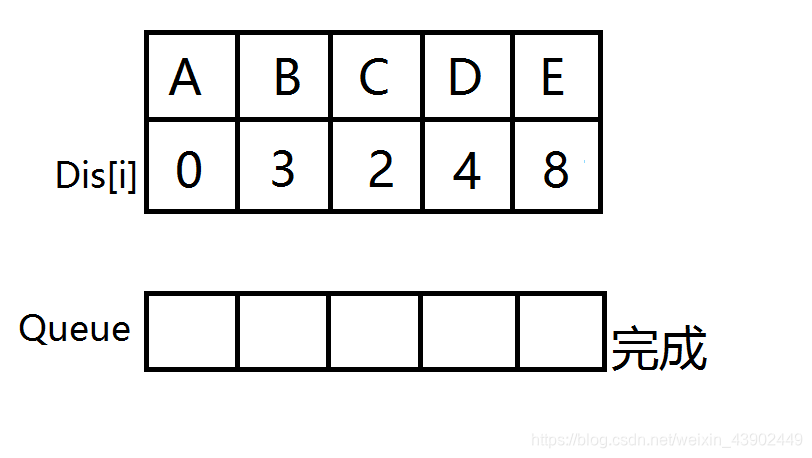
\(E\) 出队，此时队列为空，源点到所有点的最短路已被找到，\(A\to E\) 的最短路即为 \(8\)。

---

三、代码实现

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
queue<int> que;
const int N=10010,M=10010;
int n,m,tot;
int head[N],edge[M],ver[M],nxt[M],dis[N];
bool book[N];
void add(int x,int y,int z)
{
	ver[++tot]=y;
	edge[tot]=z;
	nxt[tot]=head[x];
	head[x]=tot;
}
void spfa()
{
	memset(dis,0x3f,sizeof(dis));
	memset(book,0,sizeof(book));
	dis[1]=0;
	book[1]=true;
	que.push(1);
	while(que.size())
	{
		int x=que.front();que.pop();
		book[x]=false;
		for(int i=head[x];i;i=nxt[i])
		{
			int y=ver[i],z=edge[i];
			if(dis[y]>dis[x]+z)
			{
				dis[y]=dis[x]+z;
				if(!book[y])
				{
					que.push(y);
					book[y]=true;
				}
			}
		}
	}
}
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int x,y,z;
		scanf("%d %d %d",&x,&y,&z);
		add(x,y,z);
	}
	spfa();
	for(int i=1;i<=n;i++) printf("%d ",dis[i]);
	return 0;
}

---

四、例题

模板题:hdu2680

思路:设置一个零点，将零点和所有起点的距离都设成 \(0\)，然后对零点跑一遍 SPFA 即可。

code:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
queue<int> que;
const int N=1010,M=20010;
int n,m,tot,ed;
int head[N],edge[M],ver[M],nxt[M],dis[N];
bool book[N];
#define C(n) memset(n,0,sizeof(n))
void add(int x,int y,int z)
{
	ver[++tot]=y;
	edge[tot]=z;
	nxt[tot]=head[x];
	head[x]=tot;
}
void spfa()
{
	memset(dis,0x3f,sizeof(dis));
	memset(book,0,sizeof(book));
	dis[0]=0;
	book[0]=true;
	que.push(0);
	while(que.size())
	{
		int x=que.front();que.pop();
		book[x]=false;
		for(int i=head[x];i;i=nxt[i])
		{
			int y=ver[i],z=edge[i];
			if(dis[y]>dis[x]+z)
			{
				dis[y]=dis[x]+z;
				if(!book[y])
				{
					que.push(y);
					book[y]=true;
				}
			}
		}
	}
}
int main()
{
	while(~scanf("%d %d %d",&n,&m,&ed))
	{ 
		tot=0;
		C(head);
		C(nxt);
		C(edge);
		C(ver);
		for(int i=1;i<=m;i++)
		{
			int x,y,z;
			scanf("%d %d %d",&x,&y,&z);
			add(x,y,z);
		}
		int q;
		scanf("%d",&q);
		for(int i=1;i<=q;i++)
		{
			int tmp;
			scanf("%d",&tmp);
			add(0,tmp,0);
		}
		spfa();
		if(dis[ed]!=0x3f3f3f3f) printf("%d\n",dis[ed]);
		else puts("-1");
	}
	return 0;
}