AGC
放一些我独立做不出来的并且不水的 AGC 题。
AGC005D
题意:给定 \(n,k\),求排列 \(p\) 满足 \(|p_i-i|\ne i\) 的数量,对 \(924844033\) 取模。
考虑容斥,考虑计算至少有 \(i\) 个位置不符合条件的方案。注意到每个只会与两个数产生冲突,考虑把这些冲突连上边。
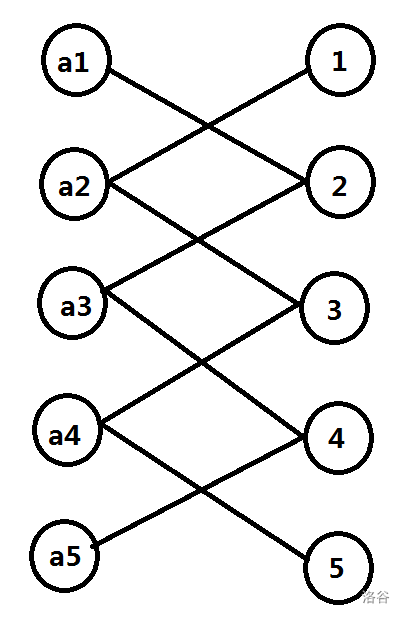
偷一张 ez_lcw 巨佬的图。
那么有一个冲突就意味着选了一条边,并且一个点连的两条边不能同时被选,即相邻的两条边至少有一个没被选。
这是一个经典问题,然后对于每个链弄出这个东西然后卷积即可,貌似也可以 dp 不过卷积貌似更容易理解和实现。
使用暴力卷积的复杂度是 \(\mathcal{O}(n^2)\),足以通过此题。
code。
AGC012C
题意:一个序列是好的当且仅当它是一个序列重复两遍,给你一个 \(n\),要求你构造一个序列使得其恰好有 \(n\) 个子序列那不至于它是好的。
长度 \(\le 200\),\(n \le 10^{14}\),数字大小 \(\le 100\)。
只想到了一个长度为 \(\mathcal{O}(\log ^2)\) 的做法:不难发现一段连续相同的贡献是 \(2^{len}-1\) 然后就做完了。
当然这个做法过不了,考虑另外一种构造,注意到长度是数字大小的两倍,可以发现如果后面的数字是 \(1,2\dots 100\),那么如果前面的排列为 \(p\),那么好的子序列的数量就是 \(p\) 的上升子序列的个数。
考虑从小到大一个一个加数,如果把空集也算作是好的,那么如果加前面则答案 \(+1\),加后面则答案 \(\times 2\),二进制拆分即可。
code。
AGC005E
首先考虑一下怎么样的情况是无解的:如果存在一个后手能到的点 \(u\),满足 \(u\) 在树 \(b\) 上存在一个相邻的点 \(v\) 满足树 \(a\) 上 \(u,v\) 的距离 \(\ge 3\),那么的话到这个点之后,反复横跳即可。
那么假定不出现这种情况,即 \(b\) 上可以到达的点连出去的边在 \(a\) 上的距离都 $ \le 2$,那么的话,一定不会出现“跨过去”的情况,这意味着每次后手都会在先手的子树内,同时他能到达的节点满足 \(depa_u > depb _u\)。那么最优的策略就是走到一个 \(depa\) 最大的点然后一直待着。
那么对于原题,先把能够让后手反复横跳的点找出来,然后如果对于前面的条件走的到这样的点,那么就输出 -1,否则就按照上述策略走。code。
AGC040C
因为考虑到每次操作是对于两个相邻的位置,那么考虑对位置奇偶取反,将所有奇数位的 \(\text{A} \to \text{B}\),\(\text{B} \to \text{A}\),那么显然每一个原序列一一对应一个新序列,而且每次删除相当于删去一个 \(\text{AA}\) 或者一个 \(\text{BB}\)。
发现后面这个问题非常好做,显然一次删除最多删掉一个 \(\text{A}\) 或者一个 \(\text{B}\),那么当 \(sum_A > \frac n 2\) 或 \(sum_B> \frac n 2\) 时必然不满足,同理可证其他情况下都满足(数归)。
那么就做完了。。容斥算不满足的个数,不妨令 \(sum_A> \frac n 2\),那么枚举 \(sum_A\) 即可。\(sum_B>\frac n 2\) 的情况乘 \(2\) 即可。code。
貌似是个套路。
AGC024E:咕
AGC001F
题目中交换的条件是 \(|i-j| \ge k,|p_i-p_j|=1\),注意到 \(|p_i-p_j| = 1\) 这个东西很诡异,若令 \(Q\) 为排列 \(P\) 的逆(即 \(Q_{P_i}=i\)),那么相当于若 \(|Q_i-Q_{i+1}| \ge k\) 就可以交换 \(Q_i\) 和 \(Q_{i+1}\),那么可以发现,若 \(|Q_i - Q_j| <k\),那么显然 \(Q_i\) 与 \(Q_j\) 在交换后的相对位置(指先后位置)是不会变的,同时可以用数学归纳法证明这是充要的。
那么再回到原排列 \(P\),相当于对于 \(|i-j|<k\),有 \(P_i\) 与 \(P_j\) 的相对大小不会变,那么的话可以得到若干个小于的关系,每次将大的向小的连边,然后拓扑排序每次删掉最大的点,那么得到的排列 \(P\) 就是最小的。
但是边数是 \(n \times k\) 级别的,考虑一个位置 \(i\) 度数为 \(0\) 的条件:\((i-k,i+k)\) 中未被删去的最大值为 \(P_i\) 那么度数就为 \(0\),同时每次删掉一个点最多使两个点度数为 \(0\),分别是 \((i-k,i)\) 的最大值的位置和 \((i,i+k)\) 的最大值的位置。这就可以用一个线段树维护,每次删点设为 \(- \infty\) 即可。
code。
AGC055C
AGC 的数数太难了。
如果知道 LIS,那么显然 \(a_i=LIS/LIS-1\),先考虑一个暴力:枚举哪些地方可以取到 \(-1\),设这个集合为 \(S\)。那么确定了 \(S\) 之后,可以猜想到可行的 \(LIS\) 是一段区间(感性理解不难吧,应该可以用调整法什么的证。。)\(LIS\) 的下界显然是 \(|S|\),并且可以通过构造取到(设 \(S\) 最后的元素为 \(x\),那么构造 \(p_{x+1 \dots n}=(n-x)\dots 1\),\(S\) 中每个元素从前往后依次从 \(n-x+1\) 递增,其余的元素从 \(n\) 递减即可)。
上界呢?考虑对于一个值为 \(LIS\) 的点,他有两种情况,一种是没有用的,另一种是有用但是有两个这样的点,删去一个无影响的,那么肯定是想让后者尽量的多,那么发现至少要两个后者这样的点才能够为 \(LIS\) 产生 \(1\) 的贡献,而且是不能够跨越两个值为 \(LIS-1\) 的点的。
那么上界就呼之欲出了:那就是每两个相邻的值为 \(LIS-1\) 的位置之间的空隙(也包括 \(0\) 与第一个位置,最后一个位置与 \(n+1\))除以 \(2\) 向下整的和加上 \(|S|\),然后我们惊讶的发现 \([l,r]\) 只与 \(|S|\) 和空隙为奇数的个数有关,枚举这两个然后用简单的组合数算贡献即可。
code。
AGC032F
代码很短的毒瘤题,这种题做了下次还是不会有个锤用,但该做还得做。。。
前置知识:在一条长度为 \(1\) 的线段里随机撒 \(n-1\) 个点形成 \(n\) 个线段,那么期望的最小为 \(\displaystyle\frac 1 {n^2}\),可以用微积分去算。
那么期望的次小呢?那就是最小加上每条边减去最小后新的长度中撒 \(n-1\) 个线段的期望最小,就是 \(\displaystyle\frac 1 {n^2}+(1-\frac 1 n)\times \frac 1 {(n-1)^2}= \frac 1 n \times( \frac 1 {n}+\frac 1 {n-1})\),可以归纳得第 \(k\) 小的期望为 \(\displaystyle \frac 1 n \times \sum_{i=1}^k \frac 1 {n-i+1}\) 。
然后考虑一个神仙的转化(这种转化感觉我一辈子都想不出来。。。):对于每一次切的地方,将这一刀设为颜色 \(1\),旋转 \(\frac 2 3 \pi\) 后再切一刀设为颜色 \(2\),再旋转 后 \(\frac 2 3 \pi\) 再切一刀设为颜色 \(3\),那么最小值就是最小的相邻的不同颜色的两刀之间的距离,正确性是比较显然的,但是 tmd 是怎么想到的啊,我不能理解。
那么的话,只考虑第一刀切出来的颜色 \(1\) 和颜色 \(2\) 那 \(\frac 2 3 \pi\) 的弧上(因为其他是对称的),那么的话相当于可以直接放到序列上:一个长为有 \(\frac 1 3\) 的线段上,线段的左右两个端点分别是 \(1\) 和 \(2\),其余的还有 \(n-1\) 个点,每个点的位置和颜色都是随机的,求两个颜色不同的点距离最短的期望。显然必然是相邻的,然后枚举第一个左右颜色不同的线段是第 \(k\) 小的线段,几率是容易算出的:\(\displaystyle \frac 1 {3^{k-1}}- \frac 1 {3^k} \times [k \ne n]\),那么答案就是 \(\displaystyle \frac 1 3 \sum _{i=1}^n (\frac 1 {3^{i-1}}- \frac 1 {3^i} \times [i \ne n]) \times \frac 1 n \times \sum_{j=1}^i \frac 1 {n-j+1}= \frac 1 n \sum_{i=1}^n \frac 1 {3^i \times (n-i+1)}\)。cmll:我会了,非常感谢。
code。都弄到这里了还需要代码吗?
AGC009D
cmll:显然只和直径有关。然后喜提一个假做法。
先把这个玩意转化成每次选一个点,把这个联通块里的权值都加一,然后删掉这个点。那么显然答案不会小于 \(\log n\) 的(每次找树的重心)。
设每个点的权值为 \(a_i\),那么有个结论:就是两个权值相同的点的路径中一定有一个权值比他大的点,这是显然的,那么 dfs 一下每次贪心的找最小的点,然后用 \(f_{u,j}\) 记录一下 \(u\) 的子树内是否有权值为 \(j\) 且他祖先里面没有权值大于 \(j\) 的点就行了,具体可以看实现。code。
AGC020F
首先肯定要断环成链:先强制最长的一条弧的起点是位置 \(0\),至于为什么是最长的文末说。
但是我们发现,每条弧的起点可能是实数,这是非常难办的,肯定要先解决掉这个问题。但是注意到弧长都是整数,那么的话,对于两种覆盖方式,如果每个弧的位置的整数部分不变,小数部分的大小关系相同,那么的话这两种覆盖方式是等价的,这启示着可以先 \((n-1)!\) 枚举剩余的弧的小数部分的大小关系(强制最长的点最小)(这里不用考虑小数部分相同的情况,显然几率是 \(0\)),显然每种关系的概率是相同的。
枚举完之后就很好做了:那么环上相当于有 \(c \times n\) 个点,每段弧有 \(c\) 个起点,然后用一个状压 dp 计数即可(\(dp_{i,S}\) 表示当前最远能到 \(i\),用了集合 \(S\),每次从前往后枚举选的点的位置即可)。时间复杂度 \(\mathcal{O}((n-1)! \times (c n)^2 \times 2^n)\),非常鬼畜。
为啥每次选最长的?如果每次不是最长的,那么有可能出现一条更长的覆盖了它并且还出头了。
code。
AGC038F
显然对于排列 \(P\) 的一个置换环,他们只有两种情况:都不变(即 \(A_i=i\)),或者都变(即 \(A_i=P_i\)),\(Q\) 也是同理,那么令 \(p_i\) 表示 \(P\) 中 \(i\) 所在的置换环的编号,\(q_i\) 同理。
那么对于一个位置 \(i\),考虑什么时候会出现 \(A_i=B_i\):
- \(i = p_i = q_i\) 那没救了,必然会出现,直接让答案减一。
- \(i = p_i \ne q_i\),那么如果 \(q_i\) 不变就会出现。
- \(i = q_i \ne p_i\),那么如果 \(p_i\) 不变就会出现。
- \(q_i=p_i \ne i\),那么如果 \(p_i\) 和 \(q_i\) 都变或者都不变就会出现。
- 其他的情况,只有 \(p_i\) 和 \(q_i\) 都不变才会出现。
但是还是不怎么可做……考虑让 \(A_i=B_i\) 的位置最少,考虑一个网络流模型:令 \(p_i\) 如果变就在集合 \(S\) 中,否则就在集合 \(T\) 中,\(q_i\) 的定义是反的,那么的话我们发现这就和文理分科这个题是很像的!
那么的话上面的那 \(4\) 种操作就可以连边了:
- \(i = p_i \ne q_i\),连 \(q_i \to T\),边权为 \(1\) 的边。
- \(i = q_i \ne p_i\),连 \(S \to p_i\),边权为 \(1\) 的边。
- \(q_i=p_i \ne i\),连 \(p_i \to q_i\) 的双向的边权为 \(1\) 的边。
- 其他的情况,连 \(q_i \to p_i\) 边权为 \(1\) 的边。
那么最小的答案就是最小割就是最大流,复杂度发现这个和二分图匹配的形式是一样的,那么就是 \(\mathcal{O(n \sqrt n)}\)。code。
AGC009E
蒟蒻只会贺题,自闭了。
考虑一次操作把选的 \(k\) 个数与新的数连边,权值为它们的平均数,那么每个数的贡献就是 \((\frac 1 k)^{h_i}\),\(h_i\) 为它的深度,那么最后的权值就是 \(\displaystyle \sum_{i=1}^m (\frac {1} k)^{b_i}\),同时有个显然的条件是 \(\displaystyle \sum_{i=1}^m (\frac {1} k)^{b_i}+\sum_{i=1}^n (\frac {1} k)^{a_i}=1\),其中 \(a_i,b_i\) 表示每个 \(0/1\) 的深度。可以证明这是充要的。
然后再 \(k\) 进制的角度下思考这个东西,相当于是数有多少个 \(w=0.x_1x_2x_3 \dots\) 满足 \(w\) 可以由 \(\displaystyle \sum_{i=1}^m (\frac {1} k)^{b_i}\) 组成并且 \(1-w\) 可以由 \(\displaystyle \sum_{i=1}^n (\frac {1} k)^{a_i}\) 组成。考虑进位的过程,对于原来的 \(\displaystyle w=\sum c_i \times (\frac 1 k)^i\) 这个形式,每次进位会让 \(\displaystyle \sum c_i\) 减少 \(k-1\),这意味着只要 \(w\) 中的 \(\displaystyle \sum x_i\le m\) 并且在膜 \(k-1\) 意义下与 \(m\) 同余即可,这也是充要的。那么 \(1-w\) 呢?貌似并不是和 \(\displaystyle \sum c_i\) 有关的?实际上还和最后一个不为零的位数 \(len\) 有关,经过简单的推导就是 \(\displaystyle len \times (k-1)-\sum c_i+1\),同理也要满足上面那个条件。然后用 \(dp_{i,j,0/1}\) 表示考虑到第 \(i\) 位,\(\displaystyle \sum c_i=j\),最后一位是否为 \(0\) 的方案数,然后用前缀和优化一下就可以了。
AGC029F
考虑一个有解的必要条件:对于一个点集的集合 \(S\),\(f(S)\) 表示这些集合的并,那么有 \(|f(S)|>|S|\),否则一定会连出环来,下面也可以说明这是必要的。
那么考虑先找一个点为根,那么其他的点一定是和与他祖先连的边一一对应的,这意味着把点与每个点集(即树上可能的边)连边,删掉任意一个点后都是有完美匹配的,那么考虑先求出来一个,然后找到没有匹配的点为根,那么所有包含当且确定的点并且本身没有被确定的边都是可以连的,可以用 bfs 一层一层扩展下去,如果能连出来一个树就是可行的,否则意味着当前没有被确定的点与没有被确定的边的个数是相同的,发现正好是上面那个无解的情况!
用 dinic 求解网络流,复杂度 \(\mathcal{O}(n \sqrt n)\)。code。
AGC007E
考虑这个要求到底是要干什么:这意味着到了一个叶子后,需要找到第一个祖先满足这个祖先内的叶子没有全部走到过,然后走到这个祖先的另一侧的儿子上去。
这便可以设计一个 dp:\(dp_{u,a,b}\) 表示 \(u\) 的子树内,起点为 \(a\),终点为 \(b\) 的情况下的最小答案。
考虑稍微转化一下状态:不记录起终点,记录起点到 \(u\) 的距离和终点到 \(u\) 的距离,那么可以二分之后扔掉一维:\(dp_{u,a}\) 表示 \(u\) 的子树内,起点为 \(a\) 的情况下终点到 \(u\) 的最小距离。
如果对于两个状态 \(a,b\),满足 \(a\le b,dp_{u,a} \le dp_{u,b}\),那么 \(b\) 完全是没有用的,把没有用的状态扔了再按照 \(a\) 排序,那么可以发现转移就是一段前缀,这样的复杂度看起来是 \(\mathcal{O(n^2 \log n)}\) 的,但是并不是如此:如果一个点左右的子树内的状态分别是 \(L,R\),那么可以发现状态数是 \(2 \times \min (L,R)\),实际上状态数总共只有 \(n \log n\) 个,那最后的复杂度就是 \(\mathcal{O}(n \log ^2n)\)。
AGC023D
神仙思维题,自闭了。
先考虑一个情况:$S<x_1 $ 或者 \(S>x_n\) ,那么的话所有人都会投相同的方向,下面考虑 \(x_n > S > x_1\) 的情况。
从后往前考虑:如果有 \(p_1 \ge p_n\),那么可以证明,\(1\) 一定在 \(n\) 前到达:如果不是这样,那么当 \(S\) 到 $x_{n-1} $ 的时候,必然会向左走,那么就有 \(t_{n}=t_1 + (x_n-x_1)\),反之亦然。
那 \(n\) 号点的所有人的决策会是如何呢?\(t_n\) 最小意味着 \(t_1\) 最小,这说明 \(n\) 号点的决策将和 \(1\) 号点是相同的,这意味着可以直接给 $p_1 $ 加上 \(p_n\),然后不考虑这个点,这就缩小到了一个更小规模的子问题,然后就做好了。
code。

