题目总结

感觉有些时候题目也做不动，而且有些题目貌似也是似懂非懂，虽然写出来了，但是未必理解，还经常要看题解。于是总结一下题目写过的题目也比颓废发呆好。

题目基本是我认为比较“好”的题或者一些经典题（当然大部分都是我不会的），思路可能会参考题解，但是也有时候就加上自己的理解，不保证不咕，主要是写给自己看的，不保证对其他人有价值。

新开了一个 CF 构造，交互，博弈题总结，以后 CF 上的构造，交互，博弈题就放在这里了，欢迎来看吖。

学长之前说过，如何想到题解的思路也是非常重要的，这里也可能会加以阐述，~~虽然我不会做~~，但会尽量去想象题解是如何想到的，考场上的灵光一现确实是解题的关键，但是灵光一现之前的准备甚至其本身的过程才是做题的作用。

如果我写的部分有错误可以直接和我说。

P4766 [CERC2014]Outer space invaders

题意：有 $n$ 个外星人，第 $i$ 个外星人在 $[l_i,r_i]$ 时段出现，需要 $d_i$ 的成本打败。在某一时刻使用 $x$ 的成本能够打败所有在该时刻出现的需要成本 $\le x$ 的外星人，求最小要多少成本。

看到数据范围想到区间 dp 与离散化，~~然后我就不会了。~~

首先离散化，使时间区间为 $[1,p]$，$dp_{i,j}$ 表示杀死出现时间 $[l,r] \in [i,j]$ 的所有外星人的最低成本，则答案为 $dp_{1,p}$，考虑转移。

如果没有外星人，那么 $dp_{i,j}=0$。
如果有外星人，那么设 $maxn_i=max(d_p)\ ([l_p,r_p]\in [i,j])$，不难得到 $dp_{i,j}=\min(dp_{i,k-1}+maxn_k+dp_{k+1,j})\ (k \in [i,j])$。

然后发现预处理 $maxn$ 数组是 $O(n^2)$ 的，时间复杂度是 $O(n^4)$ 貌似并不过的，如果用线段树维护 $maxn$ 的话也要 $O(n^3 \times logn)$，因为离散化之后 $n$ 达到了 $600$ 的规模也很难过去。（但是我并没有尝试过，可以尝试一下）。

接下来是一个比较重要的结论了：我们并不用处理 $maxn$ 数组，只要直接找到一个 $p$ 满足 $d_p$ 在所有满足条件的点中最大，这样子就能够做到 $O(n^3)$ 了。

为什么这样子是对的呢？~~绝大部分题解都没有解释，可能他们觉得这个太简单了~~。感性理解一下，枚举的这个 $k$ 就意味这在 $k$ 这个时间点上进行一次操作。那么对于 $p$，必然有一个操作是在 $[l_p,r_p]$ 之间的（为了消除 $p$），而且因为 $p$ 是最大的，那么 $maxn$ 就显然是 $d_p$ 不用预处理了。

code。

P4180 [BJWC2010]严格次小生成树经典题。

如果是非严格的最小生成树怎么做？

首先用 Kruskal 建出最小生成树，然后枚举每一条边并且加入这条边 $(u,v)$，减去树上 $(u,v)$ 这条路径上的最大边，取 $\min$ 即可。

最大边怎么求呢？用类似于 $LCA$ 求法的倍增即可。

可是严格的怎么做呢？注意到非严格的做法之所以是非严格的，是因为有可能加入的边的权值和删去边的权值相同。所以倍增的时候记录下非严格的第二大的边，倍增即可，写起来有点麻烦，但是数据强度很弱。

code。

CF981D Bookshelves

题意：给你一个数组 $a_{1...n}$，将 $a$ 划分为 $k$ 段，使每段和的按位与和最大。

首先弄个前缀和，$sum_i=\sum_{j=1}^i a_j$

因为是按位与和，所以从高到低按位考虑。若现在的答案是 $ans$，那么就要判断 $ans'=ans|2^i$ 是否可行。

那么怎么判断呢？直接判断 $ans'$ 比较困难，可以尝试判断是否存在 $x$ 满足 $x \And ans' = ans'$。有一个结论： $(a\And b) \And ans'=ans' \Leftrightarrow (a \And ans'=ans')\And (b \And ans'=ans')$。设 $dp_{i,j}$ 表示前 $i$ 个数分成 $j$ 段之后能否存在 $x$ 满足$x \And ans' = ans'$。状态转移方程为 $dp_{i,j}|=dp_{p,j-1} \And ((sum_i-sum_p) \And ans'==ans')$。其中 $dp_{0,0}=1$。

看上去到这里就结束了？其实小蒟蒻自己在做题的时候还有一个疑惑：为什么 $dp_{0,0}=1$？实际上，因为 $dp_{0,0}$ 的意义是前 $0$ 个数选 $0$ 个，后面若有一段为 $x$，那么这两段的按位与和就是 $x$（因为实际上只有一段），说明 $dp_{0,0}$ 所“代表”的数 $\And$ 任何数都是它自身。那么显然 $\And ans'=ans'$，所以 $dp_{0,0}=1$。~~可能说的并不是很好，请轻点 D 我~~。

code。

CF1491D Zookeeper and The Infinite Zoo

题意：对于点 $u$，有一条 $u \to (u+v)$ 的单向边当且仅当 $u\And v=v$，多组询问，每次给出一个 $(u,v)$，询问是否存在一条 $u\to v$ 的路径。

虽然只是 Global Round 的 D 题，但是我好菜。。。

第一个结论：若 $u>v$，则无解，原因显然。

第二个结论：对于每个 $u$，不妨每次增加一个 $v$ 满足 $v=2^i(i\in N)$。

为什么呢？如果增加的是另一个数 $x=2^{a_1}+2^{a_2}+...+2^{a_n}$，那么加 $n$ 次，第 $i$ 次加 $2^{a_i}$，显然是可行的，并且最终结果是一样的。

第三个结论：因为已知 $u \le v$，设 $v$ 中第一个为 $1$ 的数位为 $k$，那么 $u$ 中第一个为 $1$ 的数位必须 $\le k$，同时，第二，第三个都同理。即：设 $sum1_k$ 为 $u$ 在 $1-k$ 位中 $1$ 的个数，$sum2_k$ 为 $v$ 在 $1-k$ 位中 $1$ 的个数，那么对于任何时候都要有 $sum2_k\le sum1_k$。必要性显然。充分性我们可以这么构造：因为 $u \le v$，可以一位一位的把当前最高的不相同的位推到相同的，然后就可以了。建议手玩几个试一下。比如：$(011010)_2$ 和 $(100100)_2$，可以 $(011010)_2 \to (100010)_2 \to (100100)_2$。

代码就很好写了。code。

CF125E MST Company 经典题。

因为 $n \le 5000$，考虑 $n^2$ 算法。

首先断掉与 $1$ 号点连接的所有边，形成若干个联通块。对于每个联通块做一个最小生成树。然后连一条到 $1$ 号点最小的边。设有 $x$ 个联通块，如果 $x > k$ 则无解，否则还要加上 $k-x$ 条边。

对于每次加边，找到所有除去与 $1$ 连接的边后所有森林中每个点 $i$ 到当前（除去 $1$ 号点）的根最大的边 $(p1_i,p2_i)$ 以及其权值 $maxn_i$，求出边 $(1,u)$ 满足 $w-maxn_u$ 最小并且加入 $(1,u)$，删去 $(p1_u,p2_u)$。时间复杂度 $O(n^2)$。

实现比较难，有比较多的细节。code。

P3978 [TJOI2015]概率论生成函数经典题，~~可以找规律。~~

下面给出生成函数的推法：

设 $g_n$ 为 $n$ 个点的二叉树的数量，$f_n$ 为 $n$ 个点的所有二叉树的儿子的和，那么不难得到：$ans=\frac {f_n} {g_n}$。

先考虑 $g_n$ 怎么算。若左儿子的节点数为 $\displaystyle i \ (0\le i \le n-1)$，那么对于$g_n$ 的贡献为 $\displaystyle g _i \times g_{n-i-1}$，那么不难得到 $\displaystyle g_n = \sum_{i=0}^{n-1}g_i \times g_{n-i-1}$，$g_0=g_1=1$，不难发现这是个卡特兰数，即 $\displaystyle g_i=\frac{C_{2\times n}^{n}}{i+1}$。

然后考虑 $f_n$，若左节点的个数为 $\displaystyle i \ (0\le i \le n-1)$，那么左儿子对于答案的贡献为 $\displaystyle f_i \times g_{n-i-1}$，因为左右对称，所以不难得到 $\displaystyle f_n=2\times \sum_{i=1}^{n-1} f_i \times g_{n-i-1}$，这个怎么推呢？

考虑 $g_i$ 的生成函数 $G$ 以及 $f_i$ 的生成函数 $F$，那么不难得到：$G(x)=x\times G(x)^2+1,F(x)=2\times x\times F(x)\times G(x)+x$。

对于前面一个式子我们可以得到 $G(x)=\frac {1-\sqrt{1-4\times x}}{2 \times x}$ 或 $G(x)=\frac {1+\sqrt{1-4\times x}}{2 \times x}$，后者显然不是收敛的，舍去。

再通过后面一个式子可以得到：$F(x)=x \times (1-4 \times x)^{- \frac 1 2}$。

我们需要找到 $G(x)$ 和 $F(x)$ 的关系。不难发现：$\displaystyle (G(x)\times x)'=(1-4 \times x)^{- \frac 1 2}=\frac {F(x)} x$，即 $\displaystyle F(x) = x \times (G(x)\times x)'$。

则：$\displaystyle f_n=[x^n]F(x)=[x^{n-1}](G(x)\times x)'=n \times g_{n-1}=C_{2\times n-2}^{n-1}$。

$\displaystyle C_{2\times n-2}^{n-1}=\frac {(2\times n-2)!}{((n-1)!)^2}=\frac{(2\times n)!}{(n!)^2} \times \frac{n^2}{2\times n \times (2 \times n-1)}=C_{2\times n}^{n} \times\frac{n}{2 \times (2 \times n-1)}$。

那么：$\displaystyle ans=\frac {f_n}{g_n}=\frac {C_{2\times n}^{n} \times\frac{n}{2 \times (2 \times n-1)}}{\frac {C_{2\times n}^{n}}{n+1} }=\frac{n\times (n+1)}{2\times (2\times n-1)}$。

代码就不贴了。

CF708E Student's Camp 毒瘤推式子题。

首先考虑朴素的 dp：设 $dp_{i,l,r}$ 表示第 $i$ 天剩下区间 $[l,r]$ 并且合法的几率，剩下 $[l,r]$ 的几率很好算，不妨设为 $P_{l,r}$。设 $d_x$ 表示 $t$ 天中有 $x$ 个被吹走的几率，$p = \frac a b$ 为一天的几率，那么不难得到 $d_x = C_{t}^{x}\times p^x \times {(1-p)}^{t-x}$，那么显然 $P_{l,r} = d_{l-1} \times d_{m-r}$。

同时我们不难推出转移方程：$\displaystyle dp_{i,l,r} =P_{l,r} \times \sum_{[l',r'] \cap [l,r] \ne \varnothing}dp_{i-1,l',r'}$，然而这样显然是不够的，考虑优化。

使用容斥的思想不难得到：$\displaystyle dp_{i,l,r} =P_{l,r}\times \sum_{[l',r'] \cap [l,r] \ne \varnothing}dp_{i-1,l',r'} =$
$\displaystyle P_{l,r} \times (\sum_{l',r'}dp_{i-1,l',r'}-\sum_{l'\le r'<l}dp_{i-1,l',r'}-\sum _{r<l' \le r'}dp_{i-1,l',r'})$。

设 $\displaystyle f_{x,l}=\sum_{l' \le r' < l}dp_{x,l',r'}$，不难得到：$\displaystyle dp_{i,l,r}= P_{l,r} \times (f_{i-1,m} - f_{i-1,l-1}-f_{i-1,m-r})$。而且显然，$f_{n,m}$ 就是答案。

再设 $\displaystyle g_{x,r}= \sum _{l<r}dp_{x,l,r}$，那么有 $\displaystyle f_{x,l}=\sum_{l'<l}g_{l'}$。

$\displaystyle g_{x,r}= \sum _{l<r}dp_{x,l,r}=\sum_{l<r} D_{l-1} \times D_{m-r} \times (f_{x-1,m}-f_{x-1,l-1}-f_{i-1,m-r})=$
$\displaystyle D_{m-r} \times (\sum _{l<r}D_{l-1} \times (f_{x-1,m}-f_{i-1,m-r+1})-\sum_{l<r}D_{l-1}\times f_{x-1,l-1})$。

对于 $D_{i}$ 和 $D_{l} \times f_{x-1,l}$ 做一个前缀和就可以做到 $O(n^2)$ 了。

code。

CF516D Drazil and Morning Exercise

首先考虑把 $f_i$ 求出来。

~~这部分先咕了，等我找到一个说的清楚的方法再来。~~

然后我们可以观察到一个性质，找到点 $u$ 满足 $f_{u}$ 最小，那么以 $u$ 为根，对于任何 $v1$ 以及在 $v1$ 的子树中过的 $v2$，有 $d_{v1} \le d_{v2}$。

要证明这个结论，只需证明：对于任何 $v1$ 以及在 $v1$ 的儿子的 $v2$，有 $d_{v1} \le d_{v2}$。证明如下（建议画个图理解）：

$v1$ 的最长路径不经过 $v2$，那么因为 $v2$ 是 $v1$ 的儿子，那么 $v2$ 先经过 $v1$，然后走 $v1$ 的最长路径，那么显然有 $d_{v1} \le d_{v2}$。
$v1$ 的最长路径经过 $v2$，那么 $u$ 就可以先到 $v1$，然后走 $v1$ 的最长路径，即 $d_{v1} \le d_{u}$，矛盾，不可能。

综上，结论成立。

那么使用双指针，并且用并查集维护。根据结论，每次删除的点都是最外面的点，不会影响连通性，那么直接把 $size$ 减一就可以了。

code~~看代码可能更能够理解。~~

CF643F Bears and Juice 神仙题。

~~其实这是一道构造题。~~

题意：先咕了。

首先考虑，我们能够得到的“信息”是什么？

有哪些熊去睡觉了，有哪些熊没有去。
睡觉的哪些熊，他们是在什么时候睡觉的。

那么共有 $x$ 天时，我们能够得到的信息的种类数即为：$\displaystyle sum=\sum_{i=0}^{\min (p,n-1)}( \dbinom{n}{j} \times x^i)$。

解释一下这个式子：首先枚举睡觉的熊的数量 $i$，因为有 $n$ 头熊，那么有 $C_{n}^i$ 种情况。此外，睡觉的熊可以在 $1-x$ 这 $x$ 天中任选一天睡觉，那么就是 $x^i$，乘一下再加一下就可以了。

但是这个信息数只是答案的“上限”，~~因为一般来讲这个上限都是达得到的，而且你如果交一发你就会发现你过了~~，所以考虑如何构造出一种方案可以达到这个上限 $sum$。

我们把所有方案编号为 $1-sum$，酒的编号也为 $1-sum$，显然，每种方案是要恰好对应一个酒的。那么对于熊 $a$，若方案 $i$ 中他没有睡觉，那么他就不喝第 $i$ 桶的饮料。否则，如果他在 $j$ 时刻去睡觉了，那么他就在 $j$ 时刻喝第 $i$ 桶的饮料。不难发现，这样做事一一对应的。

那么我们就能够得到答案 $\displaystyle xor_{i=1}^{q} (i \times \sum_{j=0}^{\min(p,n-1)}(\dbinom{n}{j} \times i^j))\ mod \ 2^{32}$。

结果我们发现 $2^{32}$ 不是质数，$\dbinom{n}{j}$ 比较难求。注意到 $p$ 比较小，把分母里的数约掉就可以 $O(p^3)$ 预处理了。

时间复杂度 $(p^3 \times \log n + q \times p)$。

code。

CF891E Lust 生成函数，多项式。

首先观察到一个简单的结论：设一开始的数是 $a_i$（题目已经给出），结尾的数是 $a_i-b_i$（$\displaystyle 0 \le b_i\le k,\sum_{i=1}^n b_i=k$），那么这样子的答案为 $\displaystyle \prod_{i=1}^n a_i - \prod_{i=1}^n(a_i-b_i)$。

~~虽然这个结论很简单但是我还是没有发现~~。我们可以用数学归纳法证明：对于某次将 $a_x$ 减一的操作，这次操作所产生的贡献是 $\displaystyle \prod_{i \ne x,1\le x \le n}a_i=a_x\times \prod_{i \ne x,1\le x \le n}a_i-(a_x-1)\times \prod_{i \ne x,1\le x \le n}a_i$。显然成立。

那么我们只要算出 $\displaystyle \prod_{i=1}^n(a_i-b_i)$ 的期望 $E$ 就可以了。

不难得到：$ \displaystyle E = \frac 1 {n ^ k } \times k! \sum_{ b_i } ( \frac {\prod_{ i=1 }^n( a_i - b_i) }{ \prod_{i=1} ^ n (b_i !)}) = \displaystyle \frac 1 {n^k} \times k! \sum_{ b_i }( \prod_{ i = 1 }^n( \frac { a_i - b_i }{b_i!}))$。

考虑把上述式子写成生成函数的形式 $\displaystyle F_i(x)=\sum_{j=0}^{\infty}\frac {a_i-j}{j!}=\sum_{j=0}^{\infty}\frac {a_i}{j!} -\sum_{j=0}^{\infty} \frac j {j!}=(a_i-x)\times e^x$。

那么不难得到答案为 $\displaystyle [x^k](\frac 1 {n^k} \times k! \times \prod_{i=1}^n F_{i}(x))=[x^k](\frac 1 {n^k}\times k! \times \prod_{i=1}^n(a_i-x) \times e^{n\times x})$。

因为 $\displaystyle \prod_{i=1}^n(a_i-x)$ 是一个 $n$ 次多项式，$n \le 5000$ 直接暴力算出来就可以了，设 $\displaystyle \prod_{i=1}^n ( a_i - x ) = \sum_{i=0}^n f_i\times x^i$，又已知 $\displaystyle e ^{n \times x}=\sum_{i=0}^{ \infty } \frac {n^k\times x^k}{k!}$。不难有 $\displaystyle [x^k](\frac 1 {n^k}\times k! \times \prod_{i=1}^n(a_i-x) \times e^{n\times x}) = \frac {k!}{n^k} \times \sum_{i=0}^k f_i \times \frac { n^{k-i}}{(k-i)!}=\displaystyle \sum_{i=1}^k f_i \times n^{-i}\times \frac {k!}{(k-i)!}$，发现后面那个东西就是一个下降幂，提前预处理就可以了。

时间复杂度 $O(n^2)$。因为题目没给 NTT 模数而且 $n \le 5000$ 就没必要再一步优化了。

code。

P3758 [TJOI2017]可乐经典题，没看题解。

观察数据范围，考虑矩阵加速。

留在原地和去别的城市都是经典问题，直接连边就可以，难点在与自爆怎么处理，~~虽然也不是很难~~。

可以考虑新建一个点 $s=n+1$，一个点到了这里就表示他在自爆了，那么加上 $(i,s) \ (1 \le i \le s)$ 的边就可以了。接下来就是常规操作矩阵加速了。时间复杂度 $O(n^3 \log t)$。

code。

AT2046 [AGC004F] Namori 神仙题。

（本题解的图来自 @unputdownable）

首先 $n$ 为奇数显然不可能。

先考虑是一棵树的情况。树显然是一个二分图。把二分图左边的点染成黑，右边的点染成白色（即奇偶染色）。规定左边的点是黑色或者右边的点是白色的时候，这个点的真实颜色是白，否则就是黑。那么不难发现，一个合法的操作必然就是对于两个颜色不同的点交换其颜色，而最终的要求就是把所有白色换成黑色，黑色换成白色。

那么显然有白色的数量等于黑色的数量，否则不合法。

那么对于每个子树，设黑色的点与白色的点的差为 $x$，那么这个子树的根节点与其父亲之前的这条边至少要运输 $|x|$ 个点，即交换 $|x|$，那么答案的下界就是 $\sum |x|$。

~~其实我们完全可以猜测答案就是 $\sum |x|$~~。只要让每条边不进行多余的操作就行，观察一下并且感性理解一下这是做得到的。

~~其实非常的不严谨。我以后如果记得的话会补一个严谨的东西上来的。~~

实现的时候把白点设为 $-1$，黑点设为 $1$，那么记录一下子树中所有和就可以了。

那么树的情况就解决了，接下来考虑基环树的情况。

环上的点数为偶数。

先断掉一条边，然后算出子树和 $s_i$。

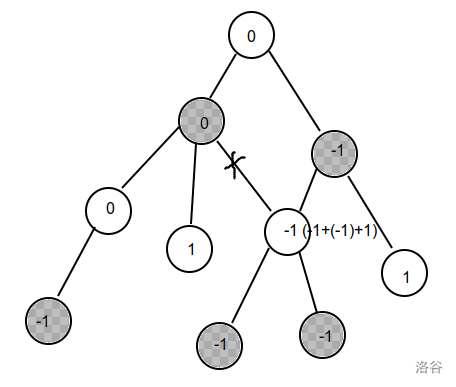
然后考虑被断掉的这条边，如果这条边运输 $x$ 的权值，那么：

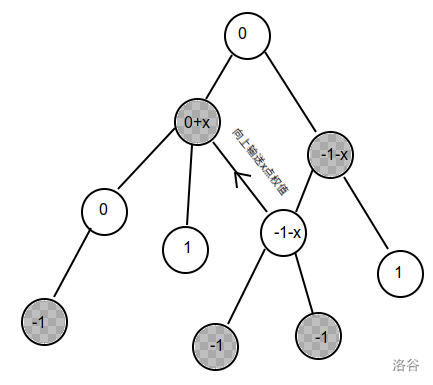
左边的点的权值为 $s_i+x$，对答案的贡献为 $|s_i+x|=|-s_i-x|$，右边的点的权值为 $s_i-x$，对答案的贡献为 $|s_i-x|$，设左边的点有一个 $k_i=-1$，右边的点 $k_i=1$。

设环上的点组成的集合为 $S$ 那么就能得到：$\displaystyle ans = \min(|x|+ \sum_{i \in S}|k_i\times s_i-x|+\sum_{i \notin S}|s_i|)$，就相当于求 $\displaystyle \min(\sum_{i \in S}|k_i \times s_i -x|+|x|)=\min(\sum_{i \in S}|k_i \times s_i -x|+|0-x|)$。这是一个经典问题。把所有的 $k_i \times s_i$ 和 $0$ 放入数组中，取中位数就可以了。

环上的点数为奇数。

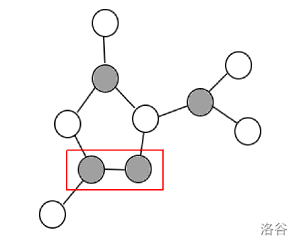
这个时候图就不是二分图了，考虑如何断掉这条边。

此时操作这条边的效果就是使黑点数量 $+2$ 或 $-2$。

那么设此时 $sum =\sum c_i$，那么可以操作 $\frac {sum} 2$ 次让它变成 $0$。

然后就转化成树的问题了。

code。

CF1119H FWT 好题。

一个非常 naive 的想法就是对于每个 $(a_i,b_i,c_i)$，设 $F_i[a_i]=x,F_i[b_i]=y,F_i[c_i]=z$，然后答案就是 $F_1 \oplus F_2 \oplus.. \oplus F_n$，其中 $ \oplus $ 表示异或卷积，时间复杂度 $O(n\times k\times 2^k)$，明显不能通过。

我们可以进行优化，对于每个 $F_i$，算出其 $FWT_i$，然后将其每项相乘再 $IFWT$ 回去，时间复杂度 $O((n+k)\times 2^k)$，还是不能通过。

我们发现每个 $F$ 只有三个数有值，考虑在这方面进行操作。

$\displaystyle \prod_{k=1}^n FWT(F_k)[i]= \prod_{k=1}^n ((-1)^{cnt(i \And a_k)}\times x+ (-1)^{cnt(i \And b_k)}\times y +(-1)^{cnt(i \And c_k)}\times z)$。

注意到上面这个东西必然只有 $8$ 种可能。然而还是太多了。不妨让 $a_i=0,b_i=b_i \oplus a_i,c_i=c_i \oplus a_i$，那么最后 $ans_{i \oplus a_1 \oplus a_2 \oplus ... \oplus a_n}$ 就是 $i$ 的答案。

这样子的话就只有 $4$ 种可能：$x+y+z,x+y-z,x-y+z,x-y-z$。设这四种出现的次数分别为 $w1,w2,w3,w4$。那么就有 $\displaystyle \prod_{k=1}^n FWT(F_k)[i]= (x+y+z)^{w1}\times (x+y-z)^{w2} \times (x-y+z)^{w3} \times (x-y-z)^{w4}$。

那么对于每个 $i$ 算出 $w1,w2,w3,w4$ 就可以得到 $\displaystyle \prod_{i=1}^n FWT(F_k)$，再 $IFWT$ 回去就可以得到答案。

那么怎么算出 $w1,w2,w3,w4$ 呢？首先不难有 $w1+w2+w3+w4=n$。

令 $F1_{k}[b_k]=1$，那么 $FWT(F1_k)[i]=(-1)^{cnt(i\And b_k)}$，设 $\displaystyle s1= \sum_{k=1}^n FWT(F1_k)[i]$，那么有 $s1=w1+w2-w3-w4$。

怎么算出 $s1$ 呢？我们有 $\displaystyle \sum_{k=1}^n FWT(F1_k)[i]= FWT(\sum_{k=1}^nF1_k)[i]$，然后就可以快速求出来了。

同理令 $F2_{k}[c_k]=1$，那么有 $\displaystyle s2=\sum_{k=1}^n FWT(F2_k)[i]=FWT(\sum_{k=1}^nF2_k)[i]$。

接下来令 $F3_{k}[b_k \oplus c_k]=1$，那么 $\displaystyle FWT(F3_{k})[i] = (-1)^{cnt(i\And (b_k \oplus c_k))}=(-1)^{cnt(i \And b_k)}\times (-1)^{cnt(i \And (c_k))}$。

那么有 $\displaystyle s3=\sum_{k=1}^nFWT(F3_k)[i]=FWT(\sum_{k=1}^n F3_k)[i]=w1-w2-w3+w4$。

那么我们就有 $4$ 个方程 $4$ 个未知数，不难手算出 $w1,w2,w3,w4$。

然后得到 $FWT(F)$ 再 $IFWT$ 回去就可以了。

code。

CF348D Turtles 容斥 dp，经典题。

首先考虑只有一只乌龟的时候怎么做，

这就是一个经典的 $dp$ 问题，设 $f_{i,j}$ 表示点 $(1,1)$ 到 $(i,j)$ 的方案数，$a_{i,j}$ 表示 $(i,j)$ 是否可走，那么有不难有：

$f_{i,j}=\begin{cases} 0\ (a_{i,j}=0) \\ f_{i,j}+f_{i-1,j}+f_{i,j-1}\ (a_{i,j}=1)\end{cases}$。

然而题目让我们求的是两条不相交的路径，这个怎么求呢？

我们不难注意到，不相交的路径必然是一条 $(1,2) \to (n-1,m)$ 的路径和一条 $(2,1) \to (n,m-1)$ 的路径，而一条 $(1,2) \to (n,m-1)$ 和一条 $(2,1) \to (n-1,m)$ 必然是相交的。那么我们因为我们能求助所有 $(1,2) \to (n-1,m)$ 的路径和 $(2,1) \to (n,m-1)$ 的路径，那么我们只要减去满足上述条件，并且相交的路径总数就可以了。

对于两条有交点的路径，不妨在最后一个交点处，交换剩下的两个路径。那么这就转换成了一条 $(1,2) \to (n,m-1)$ 和一条 $(2,1) \to (n-1,m)$ 的路径。并且不难发现，这些路径是一一对应的。所以相交的路径总数就是一条 $(1,2) \to (n,m-1)$ 和一条 $(2,1) \to (n-1,m)$ 的路径总数。

画几幅图可能更容易理解：如果原来的两条相交的路径是这样的：

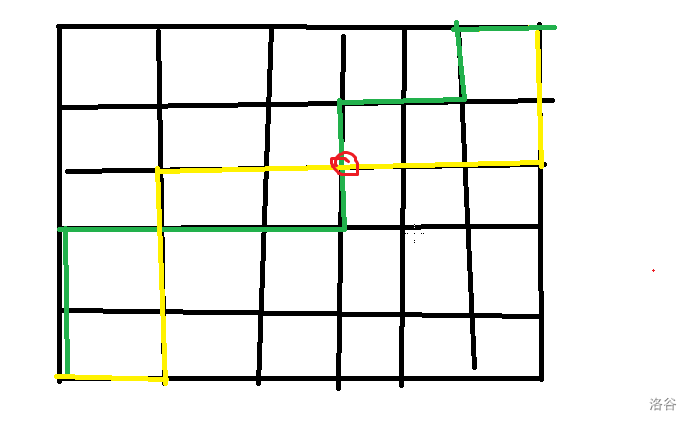
其中黄线和绿线分别表示两条路径，红圈表示最后一个交点处。那么可以讲此图转换成：

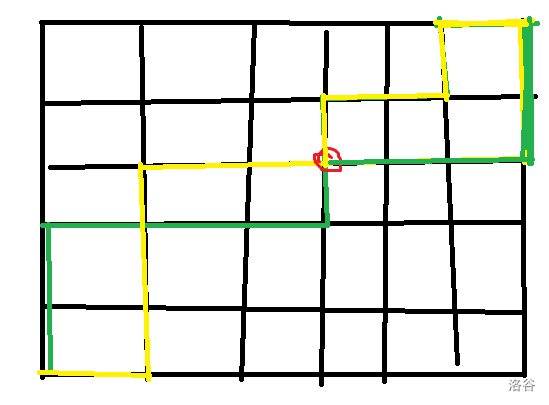
这样就是满足第二个条件的路径了。同理，每个满足第二个条件的两条路径也能够转化回来。

然后就转换成上述的经典问题了。设 $F(x1,y1,x2,y2)$ 表示 $(x1,y1) \to (x2,y2)$ 的路径总数，那么有 $ans=F(1,2,n-1,m)\times F(2,1,n,m-1)-F(1,2,n,m-1)\times F(2,1,n-1,m)$。时间复杂度 $O(n^2)$。

（吐槽：用 string 和 cin 读入字符串会被卡常）。

code。

CF727F Polycarp's problems dp。

首先不难发现，答案其实是有单调性的。具体的说，若初始的心情是 $p$，留下了 $x$ 个数，那么有 $x$ 越大，$p$ 越小（$0 \le p$）。

因为有多个询问，所以每次对二分出来的值必须快速判断，这提示我们可以预处理。

具体的说，设 $dp_{i,j}$ 表示点 $i-n$ 中，保留 $j$ 个数，所需的最小的初始值。

那么有 $dp_{i,j}=\max(dp_{i+1,j},\min(0,dp_{i+1,j-1}-a_i))$。这个式子应该很容易理解。

那么预处理出 $dp_{i,j}$ 之后，在 $dp_{1,x}$ 上二分或者把所有询问离线双指针就可以了。

code。

CF1016F Road Projects。

首先不难发现，答案不会小于原来 $1 \to n$ 的路径长度。

设 $dis_i$ 表示 $1\to i$ 的路径长度，考虑什么时候答案就是 $dis_n$。

把 $1\to n$ 的所有路径上的点拉出来形成一条链在，设这个链的集合为 $S$，那么整棵树必然是这个链上的每个节点以及其子树构成（子树可以没有）的一个树。

那么如果一个节点的子树除了它自身有超过 $2$ 个节点的话，那么取两个节点连一条边，答案就是 $m$ 个 $dis_n$ 了。

接下来考虑不是这样的情况，即一个节点的子树除了它最多只有一个节点。

不难发现，要是连 $u \to v$ 的边，如果 $u$ 有子节点 $s$，那么连 $s \to v$ 会更优， $v$ 同理。

设 $f_u$ 表示点 $u$ 到其子节点的距离。如果其没有子节点就为 $0$，那么有 $\displaystyle ans=\max_{l,r \in S,dis_l < dis_r}(x+dis_l+f_l+dis_n-dis_r+f_r)=x+ \max_{l,r \in S,dis_l < dis_r}(dis_l+f_l+dis_n-dis_r+f_r)$。发现和 $x$ 是没有关系的。预处理出 $\displaystyle \max_{l,r \in S,dis_l < dis_r}(dis_l+f_l+dis_n-dis_r+f_r)$ 就可以了。对于 $dis_l+dis_r$ 做个前缀最大值就可以了。

时间复杂度 $O(n)$。写代码的时候要注意判断 $l,r$ 能否相邻，这个自己想一想就好了。

code。

CF1146E Hot is Cold 数据结构。

因为 $a_i$ 的值域是 $[-10^5,10^5]$，而且对于 $x$，他最后只能变成 $x$ 或者 $-x$。

所以考虑用数据结构维护每个数 $x$ 最后变成了 $-x$ 还是 $x$，如果是 $-1$ 则表示为 $-x$，$1$ 则表示为 $x$。接下来考虑 $s = '>' $ 的情况。

$x \ge 0$ 的情况。

那么对于 $[-x,x]$ 的数 $a$，无论是 $-a$ 还是 $a$ 都 $\ge x$，不用进行操作。

对于 $[x+1,10^5]$ 之间的数 $a$，若是 $-a$，那么不会有变化。否则 $a$ 就会变成 $-a$，这样对于 $[x+1,10^5]$ 之间的数全部设置为 $-1$ 就可以了。同意，对于 $[-10^5,-x-1]$ 之间的是要全部设置为 $1$。

$x < 0$ 的情况。

对于 $[x+1,-x-1]$ 之间的数 $a$，无论 $a$ 上维护的值是 $1$ 还是 $-1$，都需要乘上 $-1$，即区间 $\times -1$。

对于 $[-10^5,x-1]$ 之间的数 $a$，维护的值必然会变成 $1$。对于 $[-x+1,10^5]$ 之间的数，维护的值必然会变成 $-1$。

$s='<'$ 是同理的，所以只要维护一颗能做到区间乘 $-1$，区间赋值为 $1$ 或 $-1$ 的线段树就可以了。

code。

[ZJOI2015]地震后的幻想乡概率dp，状压。

根据提示，我们可以把问题转换成：按照时间从小到大加边，排名为 $i$ 的边让这个图恰好联通的几率。

这个东西并不好求，考虑求出一个更好求的东西：排名前 $i$ 条边让这张图联通的几率。

算几率不好算，考虑算方案数。考虑状压 dp。设 $f_{i,S}$ 表示用 $i$ 条边联通 $S$ 这个集合的方案数，$g_{i,S}$ 表示用 $i$ 条边不联通 $S$ 这个集合的方案数。那么不难有 $\displaystyle f_{i,S}+g_{i,S}= \dbinom {cnt(S)}{i}$，其中 $cnt(x)$ 表示 $x$ 的二进制表示中 $1$ 的个数。

怎么转移呢？为了避免算重，这里有一个非常神仙的方法来转移。因为 $f_{i,S}$ 和 $g_{i,S}$ 只要知道一个就能知道另外一个，那么只要把 $g_{i,S}$ 算出来就可以了。首先随便钦定一个点 $p \in S$，那么有 $\displaystyle g_{i,S} = \sum_{S' \in S,S' \ne S,p \in S'} \sum_{j=0}^i f_{j,S'}\times \dbinom {cnt(S \oplus S')}{i-j}$，意思是说把原来的集合分成包含 $p$ 的一个联通块 $S'$，以及其他的点，保证 $S'$ 联通并且 $S'$ 是最大的联通快与别的点都没有连边，这样图就是不联通的。然后剩下的 $S \oplus S'$ 这个集合就随便选好了，再枚举一下每个集合的边数就可以。仔细分析一下就能发现这是不会算重的。

然后就好处理了。时间复杂度 $O(3^n \times m)$，$3^n$ 是枚举子集的时间复杂度。

code。

P3750 [六省联考2017]分手是祝愿

先考虑 $k=n$ 的时候怎么做。不难发现，必然是从大到小对于每一个亮的灯进行操作，时间复杂度 $O(n \sqrt n)$。

如果当前还需要进行 $i$ 次操作，那么显然在下一步操作中，有 $\frac i n$ 的几率让需要操作的次数 $-1$ ，有 $\displaystyle \frac {n-i} n$ 的几率让需要操作的次数 $+1$。

设 $f_i$ 表示进行 $i$ 次操作 $\to $ 进行 $i-1$ 次操作的期望时间，那么不难有 $\displaystyle f_i=\frac {n-i} n (f_{i+1}+f_i+1)+ \frac i n$，化简后得 $\displaystyle f_i=\frac {(n-i) \times f_i + n}{i}$。不难有 $f_n=1$。

算出 $f_i$ 之后我们还需要算出此时最少的操作 $cnt$，如果有 $cnt \le k$，那么答案就是 $cnt$，否则答案就是 $\displaystyle \sum_{i=k+1}^{cnt}f_i+cnt$，别忘了还要乘上 $n!$。

code。

P6669 [清华集训2016] 组合数问题数位dp。

注意到 $k$ 很小，联想到卢卡斯定理：

$\displaystyle \dbinom{i}{j} \equiv \dbinom {\frac{i}{k}}{\frac {j}{k}} \times \dbinom{i \bmod k}{j \bmod k}\pmod k$。

将 $i$ 和 $j$ 以 $k$ 进制拆分。设 $i$ 和 $j$ 的第 $p$ 位分别是 $a1_p,a2_p$，长度为 $len$，那么 $\displaystyle \dbinom {i}{j} \equiv \prod_{p=1}^{len} \dbinom{a1_p}{a2_p}\pmod k$。

又有 $a1_p,a2_p<k$，那么 $\dbinom{i}{j} \equiv0 \pmod k$ 等价于存在 $p$ 满足 $a1_p<a2_p$。用数位dp做一下就好，具体细节可以看代码。code。

CF1043F Make It One。

首先不难发现，如果答案不是无解，那么答案应该是在 $\log\log a_i$ 数量级的，手动构造一下会发现答案最大是 $7$ 的样子。

既然答案这么小，那么肯定要从这里入手。直接判断是否可行比较困难，考虑直接计算出方案。先枚举答案 $k$，设 $f_i$ 表示在 $n$ 个数中选 $k$ 个并且这 $k$ 个数的最大公约数是 $i$ 的倍数的方案数。设 $cnt_i$ 表示是 $i$ 的倍数的数的个数，那么有 $f_i = \dbinom {cnt_i}{k}$。

然后设一个 $g_i$ 表示在 $n$ 个数中选 $k$ 个并且这 $k$ 个数的最大公约数是 $i$ 的方案数，那么有 $\displaystyle g_i = f_i - \sum_{j|i,j \ne i}g_j$。$f_i$，$cnt_i$ 和 $g_i$ 都可以通过枚举倍数做到 $O(n\ln n)$ 的时间复杂度。

然而会发现这个方案数会很大，有个无脑的方法是给这个东西加个模数，理论上你的模数足够多就能保证正确性了（因为这等价于对于一个极大的模数取模，而且因为答案最多是 $7$，方案数不会非常大）。我直接用 $998244353$ 也能过。

code。

P4688 [Ynoi2016] 掉进兔子洞

（写的比较简略，如果看不懂可以问我）。

不难发现 $ans= len1+len2+len3-3\times size$，其中 $len$ 表示区间长度，$size= \sum \min(cnt1_{i},cnt2_i,cnt3_i)$，其中 $cnt_i$ 表示这个区间中 $i$ 的个数。

考虑 bitset + 莫队。

重点在于这里的离散化，应该不是很好描述但是很好理解，就用举例子来解释吧：

对于一个区间 $[1,1,4,3,3,5]$，先把它离散化成 $[1,1,5,3,3,6]$，然后对于一个询问，每次加数 $a_i$ 的时候，这个数的编号就是 $a_i+cnt_{a_i}$，$cnt_x$ 表示当前区间内 $x$ 的数量。比如：$[1,4]$ 这个区间的编号就应该是 $[1,2,5,3]$，$[3,5]$ 这个区间的编号就应该是 $[5,3,4,6]$，这很容易用莫队解决。然后把每个编号放到 bitset 里面去，不难发现三个 bitset 的交集的大小就是所求的答案。

还有一个要注意的：这个题卡空间，直接放这么多的 bitset 是放不下的，可以分段去计算。code。

P3226 [HNOI2012]集合选数好题！

考虑构造一下的矩阵：

|1|3|9|27|
|:---😐:---😐:---😐:---😐:---😐
|2|6|18|54|
|4|12|26|108|

准确的说，令 $a_{i,j}$ 表示第 $i$ 行第 $j$ 列的值，那么有 $a_{i,j}=a_{1,1} \times 2^{i-1} \times 3^{j-1}$。

那么题目要求的东西就等价于在上述矩阵中两两不相邻的方案数，注意到一行的长度大概是 $\log_3 n$ 级别的，就可以用状压 dp 解决。

而且这样子并不包含全部的数，令 $a_{1,1}$ 为所有的 $x (2 \not | x,3 \not | x)$，不难发现这是不会重复的。

顺便要加点小优化，复杂度不太会分析但是跑的蛮快的……code。

P3514 [POI2011]LIZ-Lollipop 思维题。

尝试证明下面一个结论：如果 $x$ 可以找到，那么 $x-2$ 也可以找到。

设 $x$ 所找到的区间为 $[l,r]$，那么如果 $a_l=2$ 或 $a_r =2$，那么显然，$[l+1,r]$ 或 $[l,r-1]$ 这个区间可以满足答案。

否则，就相当于 $a_l=a_r=1$，那么区间 $[l+1,r-1]$ 满足答案。

这样子的话只要找到最大的奇偶答案，然后地柜的构造就可以了。

code。

CF1151E Number of Components

不会做 *2100 的题，怀疑自己的智商有问题。

本题中一个非常重要的转换就是：联通块个数等于点数减去边数。

那么考虑点数的贡献和边数的贡献，减一下就好了。

对于一个点 $a_i$，他存在当且仅当 $l \le a_i \And r \ge a_i$，贡献是 $a_i\times (n-a_i+1)$。

对于一条边连接 $a_{i-1},a_i$，他存在当且仅当 $l \le \min(a_{i-1},a_i) \And r \ge \max(a_{i-1},a-i)$，贡献是 $\min(a_{i-1},a_i) \times (n-\max(a_{i-1},a_i)+1)$。

然后加加减减一下就好了。code。

CF1516E Baby Ehab Plays with Permutations

貌似有更快的方法，可是我不会。

考虑反着思考，设 $f_{i,j}$ 表示长度为 $i$ 的所有排列中，最少需要交换 $j$ 次可以得到原排列（$p_i=i$）的排列数，状态转移的时候可以考虑对 $p_i$ 分类讨论，如果 $p_i=i$，那么不用管它，$f_{i,j}=f_{i-1,j}$，否则，对于 $p_i = 1 \dots (n-1)$ 的情况，需要把 $p_i$ 和前面的数进行一次交换，有 $f_{i,j}=(i-1) \times f_{i-1,j-1}$，总的来说，得到 $f_{i,j}=f_{i-1,j}+(i-1)\times f_{i-1,j-1}$，一开始所有的 $f_{i,0}=1$。因为这只是最少需要的交换次数，那么交换 $i$ 次的答案就是 $f_{n,i}+f_{n,i-2}+ \dots$。看上去非常正确，只可惜时间复杂度 $O(n \times k)$，过不去。

注意到，因为最多交换 $k$ 次，那么最多有 $2k$ 的数位置会变化，可以尝试着从这里入手。一个很 naive 的想法是枚举有 $i$ 个位置变化，但是这样子做会算重。可以尝试着设 $g_{i,j}$ 表示长度为 $i$ 的所有排列中，满足 $p_l \ne l$，需要 $j$ 次交换的答案，那么交换 $x$ 次的答案就是 $\displaystyle \sum_{i=0}^{\min(n,2\times x)}(\dbinom{n}{i} \times \sum_{j=0}^{\frac x 2 } g_{i,x-2\times j})$。这样就不会算重了。

然而怎么算出 $g_{i,j}$ 呢？可以考虑在原来算出来的 $f_{i,j}$ 上做容斥。根据容斥定理就很容易得到：$\displaystyle g_{i,j}= \sum_{x=0}^i (-1)^x \times f_{i-x,j} \times \dbinom{i}{x}$。

然后就可以 $O(k^3)$ 计算出 $g$ 然后得出答案了。

code。

CF1188C Array Beauty

首先排序。这个最小值不是很好处理，转化成对于每个 $v$，最小值 $\ge v$ 的方案数，这样就相当于对于每个选出的序列 $p_1,p_2,\dots,p_k$，都有 $a_{p_i}-a_{p_{i-1}} \ge v$。然后差分一下就好了。

然后考虑 dp，设 $dp_{i,j}$ 表示最小值 $\ge v$ 时，前 $i$ 个数选了 $j$ 个，并且选了第 $i$ 个数的方案数，那么显然有 $\displaystyle dp_{i,j}=\sum_{a_i-a_k\ge v} dp_{k,j-1}$，这个东西显然可以用尺取法和前缀和优化，可以快速在 $O(n\times k)$ 的时间复杂度内完成。

再算上枚举 $v$，时间复杂度好像是 $O(\max(a_i)\times n\times k)$ 的样子，好像过不去诶…

naive！实际上，因为要选 $k$ 个数，所以显然，答案最大是 $\frac {\max(a_i)}{k-1}$ 的，枚举到这里就好了，那么最后时间复杂度不就变成 $O(\max(a_i) \times n)$ 了吗？然后就过了。

code。

CF626F Group Projects

首先先把 $a$ 排序。看到这个题目可能会想到 dp，但是如果直接 dp 的话比较难转移。设每组第一个数是 $l$，最后一个数是 $r$，那么这段区间的贡献就是 $a_r-a_l$，这提示我们可以把贡献拆开来。一个一个加数的时候，对于每一组，如果这一组里的数已经全部加完了那么就称这一组是闭合的。那么对于新加的一个数 $a_i$，有以下 $4$ 种可能：

加到了前面任何一个没有闭合的组里，这一组还是没有闭合，对总数的贡献是 $0$。
加到了前面任何一个没有闭合的组里，让这一组闭合了，对总数的贡献是 $a_i$。
新成立了一个没有闭合的组，这一组没有闭合，对总数的贡献是 $-a_i$。
新成立了一个没有闭合的组，这一组闭合了（即这一组只有它一个数），对总数的贡献是 $0$。

那么可以设 $dp_{i,j,k}$ 表示前 $i$ 个数，有 $j$ 个未闭合区间，此时的总数为 $k$ 的情况，转移就分成上面四类转移：

$dp_{i,j,k}=dp_{i-1,j,k}\times j + dp_{i-1,j+1,k-a_i} \times (j+1)+dp_{i-1,j-1,k+a_i}+dp_{i-1,j,k}=(j+1)\times (dp_{i-1,j,k}+dp_{i-1,j+1,k-a_i})+dp_{i-1,j-1,k+a_i}$。

然而……这样子会出现负下标的情况，状态数是 $n^2 \sum a_i$ 级别的，过不去。

思考一下原因：计算贡献的时候有减有加，这样的话会让第三维的下标变的很小。如果把这个过程变成单调不减的过程，那么就没有那么多事情了。

那么，怎么变呢？差分！对于 $a_r-a_l$ 这个东西，把他转化成 $\displaystyle \sum_{i=l+1}^r {a_i-a_{i-1}}$。那么算加入第 $i$ 个数之和的贡献的时候，不就相当于是 $j \times (a_{i}-a{i-1})$ 了吗（$j$ 是之前没有闭合的组，显然每个没有闭合的组都会产生 $a_{i}-a_{i-1}$ 的贡献）。

那么可以轻松得到 dp 方程（$d=a_i-a_{i-1}$）：$dp_{i,j,k}=dp_{i-1,j,k-d\times j}\times j+dp_{i-1,j+1,k-d\times(j+1)}\times (j+1)+dp_{i-1,j-1,k-d\times (j-1)}+dp_{i-1,j,k-d\times j}=dp_{i-1,j,k-d\times j}\times (j+1)+dp_{i-1,j+1,k-d\times (j+1)}\times (j+1)+dp_{i-1,j-1,k-d\times (j-1)}$。时间复杂度 $O(n^2 k)$。

code。

P4870 [BalticOI 2009 Day1]甲虫

首先，显然先排序。

有一个结论：取到的露珠必然是一段连续的区间。

证明：显然。

还有一个结论：取完一段连续的区间的所有露珠的时候，必然在最左边或者最右边。

证明：如果不在，显然会有更优的方法。

因为这个东西弄起来蛮麻烦的，正难则反，考虑最小流失多少水。

设 $dp_{i,j,0/1}$ 表示取完了 $[i,j]$ 这段区间，在最左边或者最右边时的最小流失的水的数量。转移的时候，考虑每次移动的时候的贡献（每次都想不到这个东西呜呜呜）就好（具体的来说，如果一共经过 $n$，对于第 $x$ 次次经过的点 $i$，从点 $j$ 转移过来的贡献是 $(n-x+1)\times |a_i-a_j|$），具体可以看细节。这里是 $O(n^2)$ 的。

然而有个问题，每个露珠最多减到 $0$，这怎么办呢…

枚举使用多少露珠就好啦，显然这样子会把正确的答案算进去，时间复杂度 $O(n^3)$。

还有一个细节就是一开始一点是从 $0$ 开始的，如果没有 $0$ 可以新加这一个节点进去，这样 dp 数组初始化的时候会方便。当然不这么做也是有别的方法解决的，我这里就不加阐述了。code。

~~所以，这个题里的 $m \le 10^6$ 和 $|x_i| \le 10^4$ 有任何的用处吗，害的我往 $O(nm)$ 之类的复杂度想了半天，最后还是得看题解/wq~~

CF1421E Swedish Heroes

vp 的时候大概猜到是发现这个东西的某些性质然后 dp，然而我一直在往二进制上去找规律，而且因为看到这题是 *2700，没几个人过，差不多直接就放弃了，一直没找出来/wq。

显然答案是 $\displaystyle \sum a_i \times t_i$，$t_i \in \{-1,1\}$。现在要找的就是 $t_i $ 的规律。

先摆结论：如果 $t_i=1$ 的个数为 $x$，$t_i=-1$ 的个数为 $y$，那么一段 $t_i$ 合法，需要满足 $x+2\times y \equiv 1 \pmod 3$。

证明：数学归纳法即可。我认为难点可能是想到对 3 取模，毕竟我一股脑在考虑二进制/wq。

除了这个限制还有没有别的了呢？有一个显然的：必然有两个相邻的 $t_i$ 相同。这是为了第一步。

此外就没有别的条件了。虽然我不会证明，但是想到这里大概可以大胆猜测。

然后就可以随便 dp 了，具体的过程这里就不加以阐述了，还是比较简单的。code。

CF840C On the Bench

首先，如果一个数 $a$ 可以表示为 $a=p1^{x1} \times p2^{x2} \times \dots \times pk^{xk}$ 的形式，那么令 $a = p1^{x1 \% 2} \times p2^{x2 \% 2} \times \dots \times pk^{xk \% 2}$ 显然是没有问题的。这样子的话两个数相乘是平方数等价于两个数相同。这一部分的思路还是比较显然（并且套路）的。

这样问题就转化成了相邻的数两两不相同的情况。然后考虑排序之后一个一个插入，这样可以保证相同的数会连续得被插入。然而直接计算会有点问题，因为并不需要满足时时刻刻相邻的数两两不相同。

考虑插入一个数的可能的情况。

增加了一组答案：插入在与此数相同且相邻的位置。
减少了一组答案：插入在两个相邻且相同，并且不为此数的位置。
对答案没有影响：以上两种情况之外。

如何算出以上三种的情况？我们发现需要知道当前相同且相邻的数的对数，与当前插入数相同的数的个数，与当前插入数相同且相邻的数对的个数。其中，当处理到第 $i$ 个数的时候，第二种东西是固定的。因此可以设计出一个 dp：设 $dp_{i,j,k}$ 表示当 $i$ 这个数，当前有 $j$ 对相邻且相同的数，有 $k$ 对相邻且相同且等于 $a_i$ 的数，$cnt$ 表示当前有 $cnt$ 个等于 $a_i$ 的数。推一下之后可以得到（怎么推就是时间问题了，用你喜欢的方式解决就好）：

$dp_{i,j,k}=(2\times cnt-(k-1))\times dp_{i-1,j-1,k-1}+(i-(2\times cnt-k)-(j-k))\times dp_{i-1,j,k}+dp_{i-1,j+1,k}\times (j+1-k)$。

然后转移就可以了。注意，当 $a_i \ne a_{i-1}$ 的时候，需要把所有的 $dp_{i-1,j,k}$ 加到 $dp_{i-1,j,0}$ 上，原因显然。

时空复杂度都是 $O(n^3)$。其中空间复杂度可以用滚动数组优化到 $O(n^2)$，但是没必要。

code。双倍经验（

CF1305F Kuroni and the Punishment 来道随机化放松一下（

一个显然的结论是答案 $\le n$。因为一种方法是让 $\gcd(a_i)=2$。这样最多操作次数是 $n$。

这样我们就能得到一个结论：修改次数 $\ge 2$ 的数的数量 $\le \frac n 2$。为啥是这样可以反证法，如果 $> \frac n 2$，那么答案就会超过 $n$。

所以每次随机取一个数 $i$，$a_i$ 修改次数 $\le 1$ 的几率 $\ge \frac 1 2$，即最终可能是 $a_i-1,a_i,a_i+1$。

如果已经知道了其中的一个数怎么做呢？枚举其全部质因数，并且将没有计算过的计算一次就可以了。

所以随机多次 $a_i$ 然后对于 $a_i-1,a_i,a_i+1$ 分别计算一次答案就可以了。随机 $100$ 次左右大概能随便过。

code。

P1758 [NOI2009] 管道取珠真是道好题啊！可惜我要先咕咕咕！

P4768 [NOI2018] 归程

前置知识：~~最短路~~，kruskal 重构树（建议看这个题的 kruskal 重构树做法）。

显然，对于一个询问 $(u,p)$，归程是一段 $u \to v$ 的开车的路程以及一段 $v \to 1$ 的走路的路程。前者需要满足每一步的路程都 $> p$，而后者是没有任何限制的，而且答案算的就是这一段，这意味这相当于要找到 $u$ 所有可以开车到达的点 $v$ 中，$1 \to v$ 的距离最小的那一个。后者显然是一个最短路，那就先求出 $dis_i$ 表示 $1 \to i$ 的最短路。~~注意，这题是臭名昭著的卡 SPFA 的题，请使用 dijkstra。~~

然后怎么算出来 $u$ 所有可以到达的点呢？使用 kruskal 重构树，将边按照海拔从大到小排序并且建出 kruskal 重构树，然后对于每一个 $v$，不停的向上跳，找到一个深度最小的满足海拔 $<p$ 的节点，那么这个节点的所有儿子都是可以到达的，可以在 dfs 的时候直接预处理出其所有儿子中最小的 $dis_i$，然后这个向上跳的过程是可以倍增优化的，然后就做完了！

code。

AT3526 [ARC082C] ConvexScore 非常有意思的题目！

对于一个凸包形成的点集 $S$，设其内的点集为 $T$（不包括凸包），他对于答案的贡献是 $2^{n-|S|}=2^{|T|}$，着以为这这个凸包的每个子集都会对答案产生 $1$ 的贡献，设其子集为 $P$，我们可以惊奇的发现，如果已知 $S \cup P$，那么所对应的 $S$ 和 $P$ 是唯一的，其中 $S$ 就是 $S \cup P$ 的凸包。~~这意味着每个子集都可能是答案，答案就是 $2^n$，这个题实在是太简单啦！~~

显然太 naive 了。有些点集不存在凸包，那么就需要把这些点除掉。一些点集存在凸包等价于点数 $\ge 3$ 并且三点不共线。可以 $\mathcal{O}(n^3)$ 枚举直线并找出在直线上的店，然后随便算一算就可以了。

code。

CF1264D2 Beautiful Bracket Sequence (hard version) 来补 APIO 讲的题了/youl。

先考虑 D1 （$n \le 2000$）怎么做。实际上 D1 才是解题的关键。

考虑如果已知一个括号序列，如何求其深度：对于一个点 $i$，求出 $1 \to i$ 中 ( 的数量 $a_i$，以及 $i +1 \to n$ 中 ) 的数量 $b_i$，那么显然答案就是 $\max(\min(a_i,b_i))$。

不难注意到，随着 $i$ 的增加，$a_i$ 是递增的，$b_i$ 是递减的，那么必然可以在 $a_i=b_i$ 的时候取到最大值，注意到，可能并非只有 $a_i=b_i$ 的时候取到最大值，但是，$a_i=b_i$ 必然是最大值的其中一种情况，而且因为随着 $i$ 的增加，$a_i$ 和 $b_i$ 必然会改变一个，而且当 $i=1,n-1$ 两个极端情况的时候，有 $a_i \le b_i$ 和 $b_i \le a_i$（如果答案不为 $0$，但是 $0$ 的情况本身就没有贡献不用考虑），所以会且仅仅会有一个 $i$ 取到 $a_i = b_i$，这就意味着不会算重也不会算漏了，那么做好做了。

具体的，枚举 $i$，设此时 $1 \to i$ 有 $s1$ 个 (，$s2$ 个 ?，$i+1 \to n$ 有 $s3$ 个 )，$s4$ 个 ?，其中 $s1,s2,s3,s4$ 用前缀和算一下就好。枚举当前答案是 $j$，那么此时对于答案的贡献为 $j \times \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3}$。时间复杂度 $\mathcal{O}(n^2)$。可过 D1。code1。

那么如何优化呢？后面那个式子是 $\displaystyle \sum_{j=0}^n j \times \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3}$，看起来很有优化的前途，尝试着优化一下：

\[\displaystyle \sum_{j=0}^n j \times \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3}= \\ \sum_{j=0}^n (j-s1+s1) \times \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3}=\\ \sum_{j=0}^n s1 \times \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3}+ \sum_{j=0}^n (j-s1) \times \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3} \]

先看前面这个东西：

\[\begin{aligned} \displaystyle \sum_{j=0}^n s1 \times \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3}=s1\times\sum_{j=0}^n \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3}=s1 \times \sum_{j=0}^n \dbinom{s2}{j-s1}\times \dbinom{s4}{s4+s3-j} \end{aligned} \]

考虑后面这个东西的组合意义，实际上就是 $s1\times \dbinom{s2+s4}{s4+s3-s1}$，前半部分就好了。再看看后面这个东西：

\[\begin{aligned} \sum_{j=0}^n (j-s1) \times \dbinom{s2}{j-s1}\times \dbinom{s4}{j-s3}=s2 \times \sum_{j=0}^n \dbinom{s2-1}{j-s1-1}\times \dbinom{s4}{s3+s4-j}=s2\times \dbinom{s2+s4-1}{s3+s4-s1-1}\end{aligned} \]

然后就做完了 /youl，时间复杂度 $\mathcal{O}(n\log p)$（是预处理中求逆元的复杂度），可以过 D2，code2。

CF1526E vp 的时候看到后缀数组就直接跑路了。

下文中令 $sa_i$ 为给定的后缀数组，$rk_i$ 为 $sa_i$ 的反函数，即 $suf_i$ 的排名，$suf_i$ 表示后缀 $s_{i \dots n}$。

知道 $sa_i$ 可以直接求出 $rk_i$。对于 $sa_i$ 和 $sa_{i+1}$，那么有 $suf_{sa_i} < suf_{sa_{i+1}}$，则有 $s_{sa_i} <$ 或 $\le s_{sa_{i+1}}$。

啥时候可以取到等号呢？如果 $s_{sa_i} = s_{sa_{i+1}}$ ，那么如果 $suf_{sa_i} < suf_{sa_{i+1}}$，则有 $suf_{sa_i+1} < suf_{sa_{i+1}+1}$，即 $rk_{sa_i+1}<rk_{sa_{i+1}+1}$。这个也可以直接求出来，这样就可以求出有多少个 $i$ 可以取到等号，记为 $cnt$。

然后就可以枚举取到等号的个数 $i$，在 $cnt$ 个数中找到 $i$ 个取等号的方案数是 $\dbinom{i}{cnt}$，剩下 $n-i$ 个不取等的需要在 $k$ 个字符中选择 $n-i$ 个，而且选出给定的字符集后不难确定出所有的数，方案数就是 $\dbinom{n-i}{k}$，所以最后的答案就是 $\displaystyle \sum_{i=0}^{cnt} \dbinom{i}{cnt} \times \dbinom{n-i}{k}$。

实际上这个东西根据组合意义来看就等于 $\dbinom{n}{k+cnt}$，算是一个经典的 trick，但改变不了复杂度（

#include<bits/stdc++.h>
#define int long long
#define pb push_back
#define mp make_pair
#define x first
#define y second
#define WT int T=read();while(T--) 
#define NO puts("NO");
#define YES puts("YES");
using namespace std;

inline int read()
{
    char c=getchar();int x=0;bool f=0;
    for(;!isdigit(c);c=getchar())f^=!(c^45);
    for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
    if(f)x=-x;return x;
}

const int Mod=998244353;
const int M=4e5+10;
int n,k,cnt,sa[M],rk[M],ans;
int fac[M],ifac[M];

int poww(int a,int b)
{
	int res=1;
	while(b)
	{
		if (b&1)res=res*a%Mod;
		a=a*a%Mod,b>>=1;
	}return res;
}
int inv(int x){return poww(x,Mod-2);}
int C(int m,int n)
{
	if (n<0||m<0||n>m)return 0;
	return fac[m]*ifac[m-n]%Mod*ifac[n]%Mod;
}

void init(int n)
{
	fac[0]=ifac[0]=1;
	for (int i=1;i<=n;i++)
		fac[i]=fac[i-1]*i%Mod,
		ifac[i]=inv(fac[i]);
}

signed main()
{
	n=read(),k=read();init(n+k);
	for (int i=1;i<=n;i++)sa[i]=read()+1,rk[sa[i]]=i;
	for (int i=1;i<n;i++)
		if (rk[sa[i]+1]<rk[sa[i+1]+1])cnt++;
	cout<<C(cnt+k,n)<<endl;
	return 0;
}

P6185 [NOI Online #1 提高组] 序列

很久以前的 NOI Online 的题目，非常经典。

首先另 $a_i=a_i-b_i$，那么相当于是要让最后所有的 $a_i=0$。

首先考虑一下操作 1。这意味着所有操作 1 所构成的连通块内的点直接都可以满足在总和不变的情况下任意的加减，那么就可以把这些点先缩点。

然后再考虑操作 2。将所有操作二连边，对于每个连通块，如果构成的图是一个二分图，那么显然一次操作会让二分图左边和右边的差各减一个数或者加一个数，那么方案存在等价于左边的和等于右边的和。相反，就可以在总和奇偶性不变的情况下改变任何值（在一个奇环上构造即可），也非常好判断。

code。

ARC117E

看到 $n \le 30$ 就可以考虑折半搜索或者高维 dp。折半搜索显然是不太行的（因为实际上长度是 $60$），因此可以想到这是个高维 dp。

不难想到转换成前缀和，那么有 $sum_0=sum_{2\times n}=0,|sum_i-sum_{i-1}|=1$，那么对于 $k$，设 $c_k$ 表示 $sum_i=k$ 的 $i$ 的个数 $(0 \le i\le 2\times n)$，那么有 $\displaystyle k=\sum_i \frac {c_i\times (c_i-1)}{2}$。

考虑 dp 的状态，对于这种 dp，考虑按层转移，先只考虑 $sum_i\ge 0$ 的情况，所谓“按层转移”就是对于每个 $sum$ 相同的数为一层，然后一层层去转移。状态设计时，必然会有两维分别表示当前所用掉的数的个数以及当前为 $0$ 的区间数。

（偷一张 Atcoder 官方的图片来帮助一下理解。）

然而这样直接转移是很难的，可以发现，新增的节点中必然是在每个峰之间，而且每个峰之间必须要有至少一个，那么可以把第三维状态设置成与“峰”的个数有关的东西（我代码中实际上是“峰的个数 $-1$），那么就好做了。考虑使用刷表法，每次枚举下一层的数量，然后转移即可，转移的时候相当于每两个峰（包括最左边和最右边）直接至少要有一个，剩下的自由分配，这是一个经典的组合数用隔板法弄一下就好了。

（再偷一张 Atcoder 官方的图片。）

答案怎么弄呢？一种情况就是 $sum_i \ge 0$ 那就是 $dp_{n,k,0}$，否则的话枚举 $\ge 0$ 的数字个数，所造成的贡献以及峰的个数，然后个 $<0$ 的相对应的情况乘一下再加一下就好了。时间复杂度 $\mathcal{O}(n^5)$。

code。

P3960 [NOIP2017 提高组] 列队

考虑一个 $n=1$ 的时候的做法，每次相当于取出一个点放到最后，~~我会平衡树！~~ 其实相当于是把这个位置上的数删掉然后在末尾加一个数，用树状数组/线段树维护 $0/1$ 表示这个位置有没有树，每次找第 $k$ 个的时候二分即可。

回归原问题，发现我们对于每行都要维护，但是真正改变的地方是很少的，~~我会动态开点线段树！~~ 动态开点线段树是可行的但是写起来比较困难，有个巧妙的树状数组做法。

首先离线。然后把 $x$ 相同的放在一起处理，若 $y=m$ 那么先不管，否则尝试预处理出这个 $y$ 对应的是第 $x$ 行原来的第几个位置，设为 $t$。若 $t < m$ 则显然有当前的数为 $(x-1)\times m+t$，$t\ge m$ 代表着什么意思呢？对于每一次操作 $(x,y)$，相当于把第 $(x,m)$ 个数塞入第 $x$ 行，这样的操作一共只有 $q$ 个因此可以用若干个 vector 来记录每行新塞入的数，那么 $t \ge m$ 就以为着这是第 $t-m+1$ 个新插入的数。

然后再按照时间排序，维护一下第 $m$ 列即可。具体细节可以看代码。code。

[NOIP2018 提高组] 保卫王国

暴力大家都会，直接考虑正解，~~我会 dpp！~~我不会 ddp。

考虑一个弱化版的问题：每次只钦定一个点。实际上设 $f_{u,0/1}$ 表示 $u$ 的子树内 $u$ 是否被选的最小答案，$g_{u,0/1}$ 表示整个数不考虑 $u$ 的子树并且 $u$ 是否被选的最小答案（如果 $u$ 没被选那么 $fa_u$ 是必须要选的），这两个东西都可以通过两次 dfs 求出来。

钦定两个点怎么做？注意到，钦定两个点 $(u,v)$ 之后，dp 值发生改变的只有 $u \to lca,v\to lca,lca \to rt$ 的路径，这启示我们 dp 的时候可以只考虑这些路径上的东西。$lca \to rt$ 的路径其实就是上述情况，钦定 $lca$ 选或者不选就行了，那么现在是要算出 $f'_{lca,0/1}$。

这种树上路径的题目（而且本身就需要求一个 $lca$）可以考虑倍增：具体的，令 $ff_{i,j,0/1,0/1}$ 表示 $i$ 到 $i$ 的第 $2^j$ 级祖先，$i$ 是否被选，$j$ 是否被选的情况下 $i$ 的第 $2^j$ 级祖先的子树减去 $i$ 的子树的最小答案，合并是简单的，枚举中间点是否被选取个 $\min$ 即可。

那么对于每次钦定的点 $(u,v)$，若 $u$ 为 $v$ 的祖先或者 $v$ 为 $u$ 的祖先，那么直接倍增上去即可，否则，把 $u$ 和 $v$ 都跳到 $lca$ 下一层然后枚举 $lca$ 是否被选即可，答案不难计算，具体可以看实现。code。

ARC124 E

AT 的 dp 咋都这么毒瘤……

设每个人换出去的球的个数为 $c_i$，那么若 $\min(c_i) \ne 0$，那么将所有的 $c_i-1$ 后产生的序列 $a'$ 是一样的，也显然若有 $\min{c_i}=0$，那么每个 $c_i$ 所产生的 $a'$ 也是不同的，那么的话只算 $\min(c_i)=0$ 时所有产生的 $a'$ 的贡献，这样就不会算重，也可以转化成对于所有没有限制的 $c_i$ 的贡献减去所有 $c_i>0$ 的贡献。

注意到 $\displaystyle \prod_{i=1}^n a'_i$ 表示的组合意义是有 $i$ 个盒子每个盒子有 $a_i$ 个球，从每个盒子中选一个球的方案数，第 $i$ 个球要么从第 $i$ 个盒子中剩下的取，要么从第 $i-1$ 个盒子中给出来的取，那么可以设计一个 dp：$f_{i,0/1}$ 表示处理到 $i$，$i$ 这个球是否从前一个盒子中取出，只考虑前 $i-1$ 个盒子的方案数，转移的时候枚举前一个盒子是什么样的然后算一下就行，算的时候先枚举第一个盒子的状况 $x$ 然后把 $f_{1,x}$ 设为 $1$，答案就是 $f_{n+1,x}$，还要减去 $c_i>0$ 的，具体可以看代码。

code。

ARC118E

ARC 的数数也好难。

考虑固定 $P$ 的时候怎么做，~~我会 dp！$dp_{i,j}$ 表示到 $(i,j)$ 的方案数，直接 $\mathcal{O}(n^2)$ 解决！~~显然这种做法是不好扩展的，不难想到容斥，考虑钦定经过集合 $T$ 的点，容斥系数显然是 $(-1)^{|T|}$，可以用 $dp_{i,j,k}$ 表示到了 $(i,j)$，经过了 $k$ 个不能经过的点的方案数，这种东西貌似是容易扩展的！

还是从容斥的角度去考虑，只需要考虑 $a_i = -1$ 的位置，记这样的位置个数为 $cnt$，那么对于我们钦定经过的点集的 X 坐标集合 $X$，那么剩余的集合可以随便排方案数为 $(cnt-|X|)!$，dp 的时候，发现排列（即不能重复）这个条件非常难处理，因为可以多增加两维状态：$dp_{i,j,k,0/1,0/1}$ 表示到 $(i,j)$，经过 $k$ 个不能经过的点，行/列当前有没有被填数，这样就非常好处理了，转移的时候直接避开 $a_i \ne -1$ 的点 $(i,a_i)$ 即可。

code。

ARC125E

实际上是不难想到一个网络流模型的：$s$ 向所有的人 $i$ 连一条 $c_i$ 的边，所有人 $i$ 向所有零食 $j$ 连一条 $b_j$ 的边，所有零食 $j$ 向 $t$ 连一条 $a_j$ 的边，正确性比较显然（偷一张小粉兔的图）（这张图 $n,m$ 貌似是反的）。

直接上网络流当然跑不过去，根据最大流最小割定理，我们可以把它往最小割上去考虑，即删掉若干个边让它不联通。

这里有左中右三部分边，显然如果确定了第一部分和第三部分删掉的边，那么第二部分的边也是确定的。

对于最后一部分，可以发现，若删去的边的数量相同，那么对于前面的贡献的影响是不变的，那么必然是从小到大删，排序后记录一个前缀和。

然后枚举删了 $x$ 条边，剩下 $n-x$ 个点，那么对于每个人 $i$，要么删掉 $s \to i$ 的边，贡献是 $a_i$，要么删掉所有 $i \to j$，$j$ 是未被删掉的右边的点，贡献是 $b_i \times (n-x)$，那么相当于就是 $\displaystyle \sum_{i=1}^m \min(a_i,b_i \times (n-x))$，那么当 $x$ 从往小的时候，这玩意是一个分段函数，可以记录斜率然后快速计算（具体可以看代码吧）。

[CSP-S2019] 树上的数

神仙题。。~~但该做还是得做。~~

先考虑一些特殊性质，菊花图是比较容易的，手玩一下会发现他相当于是对于每个点做了一个置换但是只能有一个环，然后每次贪心并查集急救可以了，~~听说这场几乎所有人都是 $10$ 分，那我会菊花图岂不是无敌了。~~

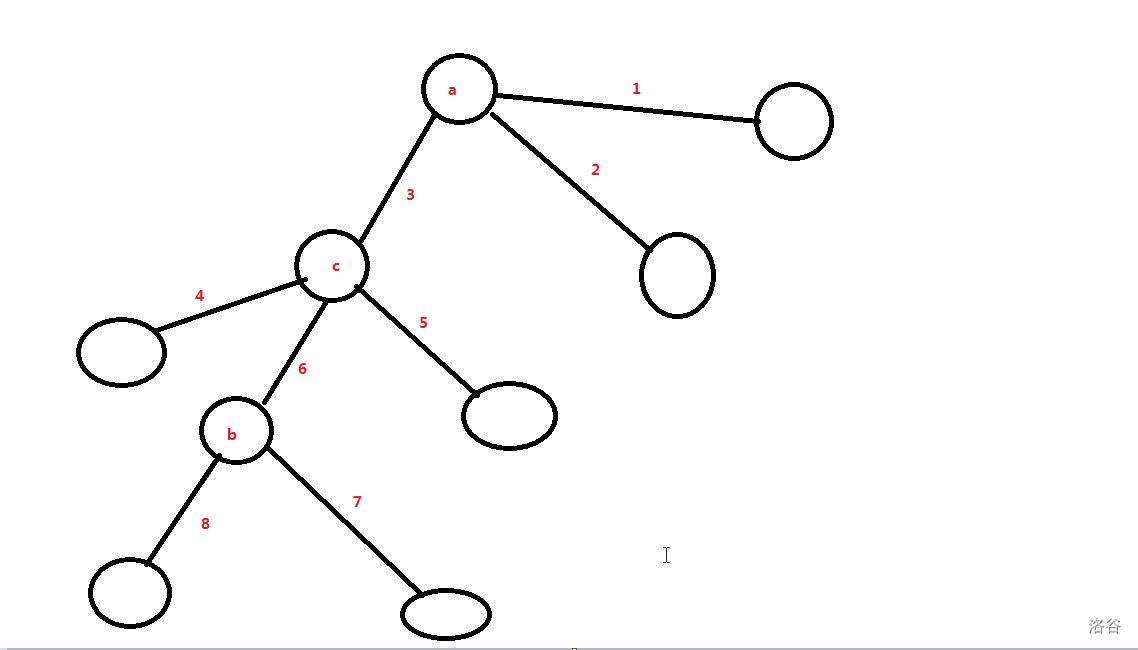
对于链的情况，先考虑从小到大的去贪心，若要把点 $a$ 上的数移到位置 $b$ 上（如图），那么对于每对相邻的边我们可以得到一些删边的先后关系：

显然，边 $2$ 比边 $1,3$ 先被删的，边 $3$ 比边 $4$ 后删，等等，那么每次暴力找到不会有矛盾的最小的点并且更新就行了。

考虑正解，注意到链的时候我们让相邻的边有个先后顺序，那么这个树的时候我们是不是也可以这样呢？答案是可以的，考虑这么一个树，若要把 $a$ 点上的数移到 $b$ 点上：

那么显然有：

与 $a$ 相邻的三条边里面，$3$ 是第一条，与 $b$ 相邻的三条边里面，$6$ 是最后一条。
对于中间经过的点 $c$，那么顺序是先 $3$ 后 $6$。

这就好了吗？显然不是：如果操作了 $3$ 之后操作了 $5$，那么 $a$ 上的数就到不了 $b$ 了，这意味着对于 $c$ 这个点连出去的边的操作，$3$ 和 $6$ 必须是相邻的。

显然每个点都可以独立来算，而且对于每个点，将连出去的边中，每次有强制要求相邻就连一条有向边，那么到最后最终的形态恰好是一条链，并且以第一条为起点，最后一条为重点。那么我们新建一个虚点，若是强制 $3$ 是 $a$ 相邻的第一条操作的边，就连这个虚点向 $3$ 的边，反之亦然，那么最终恰好是一个（有向）环（是否和菊花图的结论很像呢？），这个是很好维护的（用一个并查集记录联通性，同时用两个数组 $in,out$ 记录是否有连入/练出的边即可，形成环必须是 $sz=deg_u+1$，并查集记录一个 $sz$ 即可），注意每条边要拆成两条边，可以用一些技巧来实现，具体可以看代码。时间复杂度 $\mathcal{O}(n^2)$。

code。

[CSP-S2019] 划分

这个题看上去非常牛逼，我们掏出一个结论：每次一定选最小的可以满足的一段后缀最优，注意到每次这么操作也能让下一个可以选的最小。

怎么想到的呢？可以 dp 打表，也可以考虑一些比较小的情况然后“感性理解”。严谨的证明如下：考虑归纳法：若对于序列 $a$ 的每个前缀都满足上面的条件，那么考虑序列 $a$：

我们用红线表示每个划分，那么一定不会出现这样的情况，其中 $A$ 的最优划分为 $B$，$C$ 的最优划分为 $D$：

原因是显然的：这样的话 $D$ 可以作为 $A$ 的最优划分点，那么相当于，对于两个可行的划分点，只会有这样的情况：

（相当于除了前面多出来的若干划分点，其他的两张图中的划分点是一一穿插的）

不妨令他们划分点的个数是相同的：不同的话更加好做，因为删掉多余的那些就变成相同的了。也就是如下的情况：

那么相当于就是对于长度为 $n$ 的序列 $\{a\},\{b\}$，满足 $\displaystyle \sum a_i=\sum b_i,a_i \le a_{i+1},b_i \le b_{i+1},\sum_{i=1}^ja_i\ge \sum_{i=1}^j b_i$，证明 $\displaystyle \sum a_i^2\ge \sum b_i^2$。

考虑调整法和归纳：若有前缀相同的分割点，那么可以把他看成两部分去考虑，否则，找到第一个与 $b_1$ 相同的 $b_i$ 以及最后一个与 $b_n$ 相同的 $b_j$，令 $b_i+1$，$b_j-1$，那么平方和会变大，但是还是满足上述条件，一直归纳下去就可以了（可以证明是一定有的，而且减了之后也是满足的，比较显然qwq）。

然后就可以愉快的去做了：记录一下前缀和 $sum$ 和每个点的最优匹配 $pre$，那么对于一个点 $i$，他的最优匹配就是最大的 $k$，满足 $sum_i-sum_k\ge sum_k-sum_{pre_k}$，移项之后单调队列优化即可。略微卡空间，统计答案的时候要 __int128。code。

ARC128E

先考虑什么时候有解：把整个序列每 $k$ 个分为一块，最后一块的个数为 $x \le k$，有 $cnt$ 块，那么有解的充要条件是 $A_i \le cnt$ 并且 $\sum [A_i = cnt]\le x$。这是显然并且容易构造的。

但是要字典序最小，这个充要性的构造貌似对于本题没什么帮助。因为是字典序，那么考虑一个贪心：每次放最小的没有在前 $k-1$ 个位置出现过的数，若当前块内有 $\sum [A_i=cnt]=x$，那么必须选 $A_i=cnt$ 的位置，否则都可以，然后递归下去去做，接下来证明正确性。注意到，这么操作下去，那么每次加的数不考虑那前 $k-1$ 个的重复那是一定行的，考虑反证：

若第一个不行的位置上有 $\sum[A_i=cnt]=x$：那么相当于所有 $A_i=cnt$ 的位置上都在前 $k-1$ 个数里面出现过，那么对于前 $k-1$ 个数的情况，有 $x \to x-1,\sum[A_i=cnt]$ 不变，就矛盾了。
若第一个不行的位置上有 $\sum[A_i=cnt]<x$：那么相当于 $A_i \ne 0$ 的数都在前 $k-1$ 个里出现过了，即小于 $k$ 个。如果剩下的数 $\ge k$ 个，那么不考虑前 $k-1$ 个数的重复是可行的，那么说明 $A_i \ne 0$ 的个数至少有 $k$ 个，否则有 $cnt=1$，那么 $A_i$ 只能为 $0/1$，也是必然可以的。

然后直接贪心即可。复杂度 $\mathcal{O}(n \sum a_i)$。code。

CF1605F PalindORme

一道 div2 赛时没人过的题，评分竟然只有 2900，小编也很惊讶，可是事实就是如此。

考虑已知一个序列如何判断他是好的：容易发现第一个和最后一个一定得相同，然后这些有 $1$ 的位数可以不管，然后需要再找到不管这些位数的情况下相同的两个数。实际上这个过程等价于每次找两个能匹配的放两边。

那么考虑一个坏的序列：那么的话必然是一直操作下去，直到剩下的数中没有相同的为止。如果有 $0$ 的话就再把这个 $0$ 加进去避免算重，这样就可以让一个坏的序列对应为一个长度为 $k$ 的好的序列。

考虑一个 dp，一个朴素的想法是 $dp_{i,j}$ 表示长度为 $i$ 的序列，每个数在 $[0,2^j)$ 之间的坏的序列的个数，但是这样子实际上是难以转移的，经过尝试之后，容易注意到，第二维可以设置成所有数的或的 $\text{popcount}$。那么转移的话，枚举这个坏的序列所对应的好的序列的长度和这个序列的或的 $\text{popcount}$，然后转移的方程为 $\displaystyle dp_{i,j}=\sum_{w1,w2} (all_{w1,w2}-dp_{w1,w2})\times \dbinom{i}{w1} \times \dbinom{j}{w2} \times 2^{(i-w1)\times w2} \times f_{i-w1,j-w2}$，其中 $f(i,j)$ 表示 $i$ 个 $[1,2^j)$ 中的数，每个数最多出现一次，而且所有数的或为 $2^j-1$ 的方案数，$all_{i,j}$ 表示 $i$ 个 $[0,2^j)$ 的数组成的序列，所有的或为 $2^j-1$ 的方案数，这两个都可以容斥后预处理。时间复杂度 $\mathcal{O}(n^2k^2)$。code。

P2566 [SCOI2009]围豆豆

先考虑怎么判断一个点是否被包围了，这（貌似）是有一个经典的结论的，你弄一条横的射线出去，如果穿过了奇数次路径就被包围了，否则就没有，有些细节要弄一下，这是平凡的。

然后就可以做了，枚举起点，设 $dp_{i,j,S}$ 表示到了 $(i,j)$，当前包围的豆豆集合是 $S$ 的最短路径，由于上面那个结论，，每走一条边这个 $S$ 是可以直接弄出来的，就好了。

code。

APIO T3

考虑对于一个已知的 $x$，怎么求出答案：$dp_{u,0/1}$ 表示只考虑点 $u$ 的子树内的点，$u$ 的度数 $</ \le x$ 的最小删边方案，转移的话，需要在儿子中选出若干个连边，连边的代价是 $dp_{v,0}$，不连的代价是 $dp_{v,1}+w$。最后的答案就是 $dp_{1,1}$。转移的时候，不妨假设都连，然后不连边的贡献排序之后贪心选，这个过程是先把所有贡献小于 $0$ 的贪心加上，然后再把大于等于 $0$ 的从小到大排序加上。

考虑到一个点的度数 $deg$ 之和是 $\mathcal{O}(n)$ 级别的，而且如果 $deg_u \le x$，那么这个点位置上 $dp_{u,0}=dp_{u,1}= \sum dp_{v,1}$，对答案会造成相同的贡献可以直接加到答案上，然后直接当做他 $dp$ 值为 $0$，这就使得状态数缩减成了 $\mathcal{O}(n)$ 级别，接下来要优化的是转移的复杂度。考虑一个 $deg_u \le x$ 的节点，那么对于一个它的祖先，连上这条边的贡献就是 $w$，用一个堆来维护这些贡献，每次遍历到一个节点的时候，提前处理好的应该是已经被看成没用的点的那些 $w$ 的堆，如果这个时候堆的元素大于需要删去的边个数的时候，直接把最大的弹出来，然后对于还有用的点 dfs 并且把大于等于 $0$ 的贡献加上去，然后贪心的删最大的边直到够了位置，最后再撤销，这样的复杂度，稍微算一下就是 $\mathcal{O}(n\log n)$ 的了，不得不说是一个非常巧妙的题，~~可惜是原题~~。