数数入门

前前言

参考资料

多项式计数杂谈

【x义x讲坛】生成函数入门

膜拜巨佬

%%%太强啦 Rainbow_sjy❤OI 素质玩家孙1超

前言

首先是最基础的一些数数，相信大家都会吧。

阶乘：从 \(1\) 乘到 \(n\) 的结果，记做 \(n!\)

排列数：从 \(n\) 个不同元素中任取 \(m(m\le n)\) 个元素排成一列（考虑元素先后出现次序）称此为一个排列，此种排列的总数即为排列数，记做 \(A_n^m\) ，有 \(A_n^m=\frac{n!}{m!}\)

组合数：从 \(n\) 个不同元素中取出 \(m(m\le n)\)个元素的所有组合的个数，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的组合数，记做 \(C_n^m\) 或 \(\tbinom{n}{m}\) ，有：\(C_n^m=\frac{n!}{m!(n-m)!}\)

这些定义我们后面还可以拓展，但我们现在先不去管它。

还有一些应该知道的数学基础：

简单数学基础

简单微积分入门

导数的基本运算：

\[\begin{aligned} &(F(x)±G(x))^\prime=F^\prime(x)±G^\prime(x)\\ &(a\times F(x))^\prime=c F^\prime(x)\\ &(F(x)\times G(x))^\prime= F^\prime(x)G(x)+F(x)G^\prime(x)\\ &\left(\frac{F(x)}{G(x)}\right)'=\dfrac{F'(x)G(x)-F(x)G'(x)}{G^2(x)} \end{aligned}\]

单项式求导/求原:

\[(x^i)^\prime=ix^{i-1}\Leftrightarrow \int x^idx=\frac{x^{i+1}}{i+1} \]

链式求导法则/复合函数求导：

\[\frac{d}{du}\frac{du}{dx}=\frac{d}{dx}\\ \]

\[v(u(x))\frac{d}{dx}=v^\prime(u(x))\times u^\prime(x) \]

泰勒展开/麦克劳林级数

设 \(F^{(n)}(x)\) 为 \(F(x)\) 的 \(n\) 阶导数，我们考虑一个多项式，使其在 \(x=a\) 处零阶导数一阶导数、二阶导数……无穷阶导数与 \(F(x)\) 的对应导数相同，那么这两个函数就完全相同：

\[F(x)=\sum\limits_{i=0}\dfrac{F^{(i)}(a)}{i!}(x-a)^i \]

在 \(x=0\) 处泰勒展开

\[F(x)=\sum\limits_{i=0}\dfrac{F^{(i)}(0)}{i!}x^i \]

利用这个，我们可以用多项式表示 \(\exp x\) 、 \(\sin x\) 、 \(\cos x\)，大家可以自己试试看。

多项式牛顿迭代

若 \(G(F(x))=0\)

加入我们已知 \(G(F_0(x))=0 \pmod {x^n}\)

那么有 \(F(x)=F_0(x)-\frac{G(F_0(x))}{G^\prime(F_0(x))} \pmod{x^{2n}}\)

这个可以用泰勒展开证明：

\[G(F(x))=\frac{G(F_0(x))}{0!}+\frac{G^\prime(F_0(x))}{1!}(F(x)-F_0(x))+\frac{G^{\prime\prime}F_0(x)}{2!}(F(x)-F_0(x))^2+\ldots \]

关注 \((F(x)-F_0(x))^2\) ,发现 \(F(x)\) 与 \(F_0(x)\) 的前 \(n\) 项是相等的，最低次至少为 \(x^n\) ,平方后就是 \(x^{2n}\)，再取模是把它给“截断了”

化简就能得到一开始的结论了。

例题1：一个方程

Using the chain rule is like peeling an onion: you have to deal with each layer at a time, and if it is too big you will start crying。

这里化一个比较麻烦的方程，等下可能会用到：
\(G(x)=x\exp \frac{2F(x)-F(x)^2}{2-2F(x)}-F(x)\)

我们让 \(G(x)\) 对 \(F(x)\) 求导，可以得到：

\[G^\prime(F(x))=x\times \exp \frac{2F(x)-F(x)^2}{2-2F(x)}\times (\frac{2F(x)-F(x)^2}{2-2F(x)})^\prime-1= \]

为了让推导更加简洁，我们令\(H(x)=x\times \exp \frac{2F_0(x)-F_0(x)^2}{2-2F_0(x)}\)，然后就可以列出迭代式了：

\[\begin{aligned} F(x)&=F_0(x)-\frac{G(F_0(x))}{G^\prime(F_0(x))}\\ &=F_0(x)-\frac{H(x)-F_0(x)}{H(x)\times (\frac{2F_0(x)-F_0(x)^2}{2-2F_0(x)})^\prime-1}\\ &=F_0(x)-\frac{2H(x)-2F_0(x)}{(1+\frac{1}{(F(x)-1)^2})H(x)-2} \end{aligned}\]

中间跳去的步骤留给读者自己思考我绝对不会说是编辑器太卡了

阶乘幂引入

下降幂 :

\[x^{\underline{n}}=\overbrace{x(x-1)(x-2)\ldots(x-n+1)}^{\text{共}n\text{个因子}} \]

注意当 \(n<0\) 时下降幂仍有意义：

\[x^{\underline{-n}}=\dfrac{1}{(x+1)(x+2)\ldots(x+n)} \]

上升幂：

\[x^{\overline{n}}=\overbrace{x(x+1)(x+2)\ldots(x+n-1)}^{\text{共 n 个因子}} \]

类似的有 \(n<0\)

\[x^{\overline{-n}}=\dfrac{1}{(x-1)(x-2)\ldots(x-n)} \]

两者统称为阶乘幂。

有一些简单的性质：

\[x^{\overline{a+b}}=x^{\overline{a}}(x+a)^{\overline{b}} \]

\[x^{\underline{a+b}}=x^{\underline{a}}(x-a)^{\overline{b}} \]

以及上升幂与下降幂的转化：

\[x^{\overline{n}}=(-1)^n(-x)^{\underline{n}} \]

\[x^{\underline{n}}=(-1)^n(-x)^{\overline{n}} \]

来考虑前者：

\[\begin{aligned} x^{\overline{n}}&=x(x+1)(x+2)\ldots(x+n-1)\\ &=(-1)^n(-x)(-x-1)(-x-2)\ldots(-x-n+1)\\ &=(-1)^n(-x)^{\underline n} \end{aligned} \]

一些有趣的性质由于笔者还不会就咕咕咕了。

广义二项式系数&广义二项式定理

二项式定理：

\[(x+y)^n=\sum_{i=0}^n\tbinom{n}{i}x^iy^{n-i} \]

\(\tbinom{n}{m}\) 表示 \(n\) 个里选 \(m\) 个的方案数

\[\tbinom{n}{m}=\frac{n!}{m!(n-m)!} \]

此时要求 \(n,m\) 都为整数且\(m\le n\)。可以换一种写法：

\[\tbinom{n}{m}=\frac{n^{\underline{m}}}{m!} \]

显然正确。

现在我们的组合数对于实数也有意义了。因为对于实数为底并不影响下降幂的计算。

现在我们的二项式定理的 \(n\) 也就不再局限于正整数了。用 \(\alpha\) 重写柿子，区分一下上式 （其实因为博客里都是α

\[(x+y)^\alpha=\sum_{i=0}^\infty \tbinom{\alpha}{i}x^iy^{n-i} \]

普通的二项式只要取到 \(n\) 是因为后面的下降幂会变成 \(0\)

只需证明 \((1+z)^\alpha=\sum_{i=0}^\infty \tbinom{\alpha}{i}z^i\) ，然后令 \(z=\frac{x}{y}\) ,两边同乘 \(y^\alpha\) 即可。

不难发现

\[\begin{aligned} ((1+z)^\alpha)^{(i)} &=(\alpha(1+z)^{\alpha-1})^{(i-1)}\\ &=(\alpha(\alpha-1)(1+z)^{\alpha-2})^{(i-2)}\\ &=\ldots\\ &=\alpha^{\underline{i}}(1+z)^{\alpha-i} \end{aligned} \]

于是带入麦克劳林级数得到：

\[(1+z)^\alpha=\sum_{i=0}^\infty\frac{\alpha^{\underline{i}}}{i!}z^i=\sum_{i=0}^\infty\tbinom{\alpha}{i}z^i \]

不过要注意当 \(z\not\in(-1,1)\) 时上式发散，不过求系数倒是不影响。

上指标反转

\[\tbinom{r}{k}=(-1)^k\tbinom{k-r-1}{k} \]

理解：两数分母字样，分子\(r^{\underline{k}}=(-1)^k(-r)^{\overline{k}}=(-1)^k(k-r-1)^{\underline{k}}\)

接下来就可以进行一些魔法了

\(\tbinom{2n}{n}\)的封闭形式

\[\sum_{n=0}^\infty\tbinom{2n}{n}x^n \]

考虑下降幂的定义，我们发现

\[\begin{aligned} x^{\underline{k}}(x-\frac12)^{\underline{k}}&=\frac{2x\times (2x-2)\times\ldots\times (2k-2k+2) \times (2x-1)\times(2x-3)\times\ldots\times(2x-2k+1)}{2^{2k}}\\ &=\frac{2x\times (2x-1)\times (2x-2) \times(2x-3)\times\times\ldots\times(2k-2k+2)\times(2x-2k+1)}{2^{2k}}\\ &=\frac{(2x)^{\underline{2k}}}{2^{2k}} \end{aligned}\]

令 \(x=k=n\) ，得到：\(n^{\underline{n}}(n-\frac12)^{\underline{n}}=\frac{(2n)^{\underline{2n}}}{4^n}\)

考虑用拆开右边的 \((2n)^{\underline{2n}}=(2n)^{\underline{n}}n^{\underline{n}}\)

于是两边就可以消去一些东西了：\((n-\frac12)^{\underline{n}}=\frac{(2n)^{\underline{n}}}{4^n}\)

两边同除 \(n!\) 得到我们喜闻乐见的组合数：\(4^n\tbinom{n-\frac12}{n}=\tbinom{2n}{n}\)

用一下我们刚刚的指标反转：\(4^n(-1)^n\tbinom{-\frac12}{n}=\tbinom{2n}{n}\)

于是我们就可以来化简了 \( \sum_{n=0}^\infty\tbinom{2n}{n}x^n=\sum_{n=0}^\infty\tbinom{-\frac12}{n}(-4x)^n\)

于是我们可以得到一个非常优美的柿子：

\[\sum_{n=0}^\infty\tbinom{2n}{n}x^n=\frac{1}{\sqrt{1-4x}} \]

这个柿子我们后面还会用到。

生成函数

对于一个数列 \(a_0,a_1,a_2,\ldots\) ，我们可以搞一个函数来描述这个序列，然后就可以用一些数学魔法来解决一些问题。形式化地，我们定义：

\[F(x)=a_0f_0(x)+a_1f_a(x)+a_2f_2(x)+\ldots \]

这里的 \(f_k(x)\) 我们随便搞出来的标志函数。我们称 \(F(x)\) 为数列 \(\{a_0,a_1,a_2,\ldots\}\) 的母函数，也称为生成函数。

那么现在我们只需要研究函数就可以解决一些实际问题了。

普通生成函数 \(\mathbf{OGF}\)

如果我们定义 \(f_k(x)=x^k\) ，就能得到最普通的一类生成函数，即普通生成函数（\(\mathbf{OGF}\)，\(\rm ordinary\quad generating\quad function\)），来看一下这个奇怪的函数：

\[F(x)=a_0+a_1x^1+a_2x^2+\ldots \]

例题1：简单背包问题

现在我们先来看一个简单例题：有 \(\rm 1g\) 的砝码三个， \(\rm 3g\) 的砝码一个， \(\rm 5g\) 的砝码一个，求凑出 \(\rm 10g\) 的方案数。

当然可以背包，但从生成函数来看，这个答案就是 \((1+x+x^2+x^3)(1+x^3)(1+x^5)\)的\(x^{10}\)的系数，记为 \([x^{10}](1+x+x^2+x^3)(1+x^3)(1+x^5)\)。

上边的问题为什么可以这么求解？其实本质还是因为多项式乘法：

\[[x^n](F(x)\times G(x))=\sum_{i=0}^nF_iG_{n-i} \]

就类似于 \(\rm dp\) 的思想， 根据乘法原理，\(n\) 的方案数来自于就是两个子问题的方案，且与多项式乘法惊人地吻合。想通了这一点，上面的例题也就迎刃而解了。

现在来看几个常用的普通生成函数：

\[\boxed{ \begin{aligned} &\{1,1,1,1,\ldots\}\stackrel{\mathbf{OGF}}{\longrightarrow}\frac{1}{1-x}\\ &\{\overbrace{1,1,1,\ldots,1}^n\}\stackrel{\mathbf{OGF}}{\longrightarrow}\frac{1-x^{n+1}}{1-x}\\ &\{0,1,0,1,\ldots\}\stackrel{\mathbf{OGF}}{\longrightarrow}\frac{x}{1-x^2}\\ &\{1,c,c^2,c^3,\ldots\}\stackrel{\mathbf{OGF}}{\longrightarrow}\frac{1}{1-cx}\\ \end{aligned} } \]

这里只证明第二个柿子（逃：

\[\begin{aligned} 1+&x+x^2+\ldots+x^{n-1}+x^n=S&(1)\\ &x+x^2+\ldots+x^{n-1}+x^n+x^{n+1}=xS&(2)\\ \end{aligned} \]

\((2)-(1),x^{n+1}-1=(x-1)S\)，即\(S=\frac{1-x^{n+1}}{1-x}\)。

发现若是 \(x\in(-1,1)\) :

\[\lim_{n\to +\infty}\frac{1-x^{n+1}}{1-x}=\frac{1}{1-x} \]

这也就证明了第一个柿子。

但现在的左右两边只有当\(x\in(-1,1)\)才成立。但我们做生成函数只考虑系数，不用管范围。

其他柿子都是同理。

例题2：斐波那契数列

记斐波那契数列的第 \(i\) 项为 \(fib_i\) ，那么有： \(fib_0=0,fib_1=1,fib_n=fib_{n-1}+fib_{n-2}\)

令 \(F(x)=\sum_{i=0}^{+\infty}fib_ix^i\) ，即 \(\mathbf{OGF}\{fib_0,fib_1,fib_2,\ldots\}\)：

\[\begin{alignedat}{2} F(x)&=fib_0+&fib_1\times x+&fib_2\times x^2+fib_3\times x^3+fib_4\times x^4+\ldots(1)\\ xF(x)&=&fib_0\times x+&fib_1\times x^2+fib_2\times x^3+fib_3\times x^4+\ldots(2)\\ x^2F(x)&=&&fib_0\times x^2+fib_1\times x^3+fib_2\times x^4+\ldots(3)\\ \end{alignedat} \]

\((2)\) 式加 \((3)\) 式，由于 \(fib_i+fib_{i+1}=fib_{i+2}\) ，可以得到：

\[(x+x^2)F(x)=fib_2\times x^2+fib_3\times x^3+fib_4\times x^4\ldots \]

与 \((1)\) 式对比一下，有：

\[F(x)=(x+x^2)F(x)+x \]

可以得到一个非常优美的柿子：

\[F(x)=\frac{x}{1-x-x^2} \]

称之为封闭形式。

利用这个我们甚至还可以反推通项公式：

设 \(x_{1,2}\) 为方程 \(x^2+x-1=0\) 的两根，那么就可以把 \(\frac{x}{1-x-x^2}\) 化为我们喜闻乐见的 \(\frac{1}{1-cx}\) 的形式：

\[\begin{aligned} F(x)&=-\frac{x}{x^2+x-1}=-\frac{x}{(x-x_1)(x-x_2)}\\ &=\frac{x}{x_1-x_2}(\frac{1}{x-x_1}-\frac{1}{x-x_2})\\ &=\frac{x}{x_1-x_2}(-\frac{1}{x_1}\frac{1}{1-x/x_1}+\frac{1}{x_2}\frac{1}{1-x/x_2})\\ &=\frac{1}{x_1-x_2}( -\frac{1}{x_1}\sum_{i=0}^\infty \frac{x^{i+1}}{x_1^i} +\frac{1}{x_2}\sum_{i=0}^\infty \frac{x^{i+1}}{x_2^i} )\\ &=\frac{1}{x_1-x_2}( -\sum_{i=1}^\infty \frac{x^i}{x_1^i} +\sum_{i=1}^\infty \frac{x^i}{x_2^i} ) \end{aligned} \]

提取系数得到 \([x^n]F(x)=\frac{1}{x_1-x_2}(\frac{1}{x_2^n}-\frac{1}{x_1^n})\) ，把 \(x_{1,2}\) 带入，得到了大名鼎鼎的斐波那契通项公式：

\[fib_n=\dfrac{\sqrt{5}}{5}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right] \]

思考题： \(G(x)=\frac{1}{x^2+1}\) ，求 \([x^n]G(x) \bmod 998244353\)

例题3：卡塔兰数

\(C_0=1,C_n=n\text{对括号合法序列数}\) \((n>1)\)

口胡出递推方程：

\[C_{n+1}=\sum_{i=0}^nC_iC_{n-i} \]

也就是枚举第一对括号里放了多少东西。

来考虑 \(C_i\) 的生成函数 \(C(x)\) ,发现：

\[xC^2(x)+1=C(x) \]

就是\(C(x)\)自卷、右移一位(对应\(n+1\))、强制令\(C_0=1\)

我们用自身表示了自己，根据求根公式不难得到：

\[C(x)=\dfrac{1±\sqrt{1-4x}}{2x} \]

现在出现了两个根，应该取哪一个呢？根据定义，对于一个\(\mathbf{OGF}\) ,当\(x\to0\)时应该是收敛的，那么我们来验证一下：

• \(\displaystyle \lim_{x\to0}\dfrac{1+\sqrt{1-4x}}{2x}\)显然不收敛。
• \(\displaystyle \lim_{x\to0}\dfrac{1-\sqrt{1-4x}}{2x}=1\)。

不难知道选负号。

然后提取系数\([x^n]\dfrac{1-\sqrt{1-4x}}{2x}\)

如果你阅读了前面的话应该知道 \(\displaystyle \sqrt{1-4x}=\sum_{n=0}^{+\infty}\tbinom{\frac12}{n}(-4x)^n\)

提取系数就可以发现我们需要的了 \(C[n]=-\frac{(-4)^{n+1}\tbinom{\frac12}{n+1}}{2}\)

可以拆广义二项式系数。最终得到：

\[C[n]=\frac{\tbinom{2n}{n}}{n+1} \]

我们又双叒叕推出了一个（伪）通项。

例题4：差分与前缀积

这个我熟，我会 \(\Theta(nk)\)

考虑一个数列 \(\langle a_0,a_1,a_2,\rangle\) ，对其 \(\mathbf{OGF}\) 做前缀和和差分的结果。

记当前的生成函数为\(F(x)\)

对于前缀和，发现 \(a_n^\prime=\sum_{i=1}^na_i\times 1\) ，那么构造一个生成函数\(G(x)=1+x+x^2+\ldots\)，就有：

\[F^\prime(x)=F(x)\times G(x) \]

(这里的 \(F^\prime(x)\) 指做完前缀和后的生成函数)

我们知道乘法具有结合律，因此做完 \(k\) 次后的生成函数就为 \(F(x)\times G^k(x)\)

对于前缀积，发现

\[F^\prime(x)=F(x)-xF(x)=F(x)\times(1-x) \]

可以理解为：\(xF(x)\) 可以理解为把整个数列右移。

于是也可以写成幂形式： \(F(x)\times(1-x)^k\)

都看到这里了写个多项式快速幂应该难不倒你吧QwQ

指数生成函数 \(\mathbf{EGF}\)

我们令 \(f_k(x)=\frac{x^k}{k!}\) 就可以得到指数生成函数（\(\mathbf{EGF}\)，\(\rm exponential\quad generating\quad function\)）了。

\[F(x)=a_0+\frac{a_1x}{1!}+\frac{a_2x^2}{2!}+\frac{a_3x^3}{3!}+\ldots \]

首先来看一个数列 \(\{1,1,1,\ldots\}\)，ta的 \(\mathbf{EGF}\) 就为

\[F(x)=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\ldots \]

惊奇的发现：这不就是 \(e^x\) 的泰勒展开吗。这也是指数其名字的由来。来看几个比较简单的生成函数：

\[\boxed{ \begin{aligned} &\{1,1,1,1,\ldots\}\stackrel{\mathbf{EGF}}{\longrightarrow}e^x\\ &\{1,-1,1,-1,\ldots\}\stackrel{\mathbf{EGF}}{\longrightarrow} e^{-x}\\ &\{1,0,1,0,\ldots\}\stackrel{\mathbf{EGF}}{\longrightarrow} \frac{e^x+e^{-x}}{2}\\ &\{0,1,0,1,\ldots\}\stackrel{\mathbf{EGF}}{\longrightarrow} \frac{e^x-e^{-x}}{2}\\ &\{1,c,c^2,c^3,\ldots\}\stackrel{\mathbf{EGF}}{\longrightarrow} e^{cx} \end{aligned} } \]

都可以用泰勒展开得到。

那么指数生成函数有什么意义呢？

例题1：数数问题

用两个\(1\)，两个\(3\)，一个\(5\)，能排成多少个不同的四位数？

\[\mathbf{EGF}\{1,1,1\}\times\mathbf{EGF}\{1,1\}\times\mathbf{EGF}\{1,1\} \]

提取 \(\frac{x^4}{4!}\) 的系数即为答案。

还是考虑多项式乘法，我们设\(A(x)\times B(x)=C(x)\)：\(\frac{C_n}{n!}=\sum_{i=0}^n\frac{A_i}{i!}\frac{B_{n-i}}{(n-i)!}\)，可以写成组合数的形式：

\[C_n=\sum_{i=0}^n\tbinom{n}{i}A_iB_{n-i} \]

可以理解成对 \(A\) 、 \(B\) 内部的方案放到大小为 \(n\) 的序列中，对其中 \(i\) 个位置选用 \(A\) 内部的方案，剩下的位置选用 \(B\) 的方案。在回顾例题就迎刃而解了。

例题2：染色问题

用红蓝绿三种颜色，涂一个长度为 \(n\) 的纸条，使得红色和蓝色的个数是偶数，求方案数。

这显然符合我们刚刚的 \(\mathbf{EGF}\) ，分别考虑三种颜色的:

• 红色和蓝色是偶数 \(\{1,0,1,0,\ldots\}\stackrel{\mathbf{EGF}}{\longrightarrow} \frac{e^x+e^{-x}}{2}\)
• 绿色是任意数 \(\{1,1,1,1,\ldots\}\stackrel{\mathbf{EGF}}{\longrightarrow}e^x\)

把这三者乘起来就是答案的 \(\mathbf{EGF}\) 了

\[(\frac{e^x+e^{-x}}{2})^2e^x=\frac{e^{3x}+2e^{x}+e^{-x}}{4} \]

提取系数(也可以理解为还原 \(\mathbf{EGF}\) )得到：\(\frac{3^n+2+(-1)^n}{4}\)

例题3：无聊的水题 I

有一说一确实又无聊又水

一棵有编号无根树唯一对应一个prufer序列，并且，度数为其在序列中的出现次数加 \(1\) 。我们希望能求出满足的序列数使其出现的最大次数为 \(M-1\)。

最大次数恰好为 \(M-1\) 不太好做，考虑差分：

• \(\text{至多M-1次}-\text{至多M-2次}=\text{恰好M-1次}\)

于是剩下的就是套路了。

于是对每一个节点写出在序列中的 \(\mathbf{EGF}\):

\[F(x)=\sum_{i=0}^m\frac{x^i}{i!} \]

每个节点的生成函数都是一样的，答案的生成函数就是\(F^N(x)\)。

对于\(m=M-1,M-2\)分别求值做差即可。

概率生成函数 \(\mathbf{PGF}\)

概率生成函数与上面两种略有不同，先来看一下概率生成函数(\(\mathbf{PGF}\),\(\rm probabilistic\quad generating\quad function\))

设 \(P(A)\) 为 \(A\) 为真的概率。

对于一个离散随机变量 \(X\):

\[F(x)=\sum P(X=i)x^i \]

这个不太好看的柿子有很多神奇的结论：

1. 根据定义显然有 \(\sum P(X=i)=1\)，即\(F(1)=1\)
2. \(E(X)=\sum_{i}P(X=i)i=F^\prime(1)\)
3. 方差也咕咕咕了

其实等于号可以改成大于号，不过上面的性质就不满足了。

很多时候概率生成函数只是一个工具，实际使用中最后的结果往往与其无关。

直接看例题吧。

例题1：[CTSC2006]歌唱王国

设 \(F_i\) 为恰好到第 \(i\) 次结束的概率，\(G_i\) 表示到第 \(i\) 次还未结束的概率。\(F(x)\) 、 \(G(x)\) 分别为两者的 \(\mathbf{PGF}\)

那么唱一个数，要么结束要么没结束，因此有：

\[F(x)+G(x)=xG(x)+1 \]

对比系数，左边 \([x^n]\) 表示 \(n\) 次恰好结束与 \(n\) 次还未结束的概率，右侧 \([x^n]xG(x)=G[n-1]\) ,就是 \(n-1\)次未结束的概率。因为一定会结束，所以两者相等。

两边同时求导：

\[\begin{aligned} F^\prime(x)+G^\prime(x)&=xG^\prime(x)+G(x)\\ F^\prime(1)&=G(1) \end{aligned} \]

利用到字符串本身的一些性质。对于序列 \(A\)，如果 \(A[1:i]=A[len-i+1:len]\) ，即又是前缀又是后缀，那么称其为一个 \(\rm border\)。

能够写出一个奇怪的等式：

\[G(x)\times(\frac1mx)^L=\sum_{A[1:i] \rm is\ border}F(x)\times(\frac1mx)^{L-i} \]

左边是强制令其结束，右边是因为强制结束时可能已经结束，此时必定最后是一个 \(\rm border\) (可以画个图理解一下)

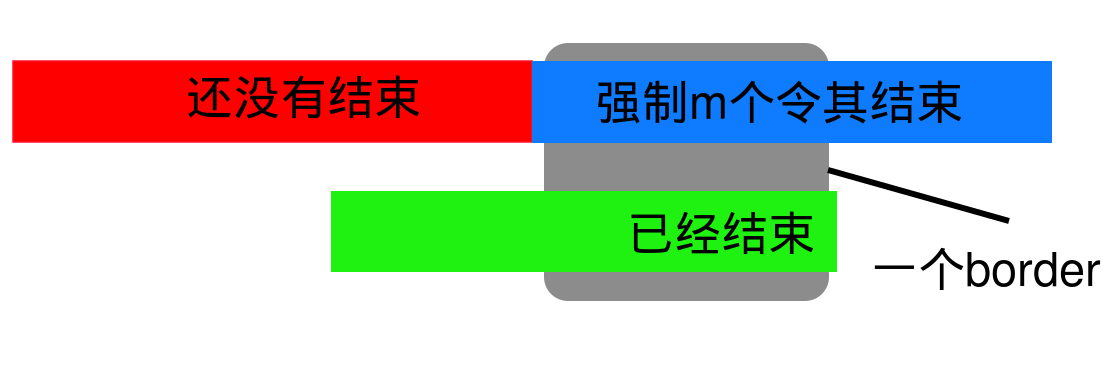
那么把 \(x=1\) 就可以出答案了

\[F^\prime(1)=G(1)=\sum_{A[1:i]\rm is\ border}F(1)m^i=\sum_{A[1:i]\rm is\ border}m^i \]

然后hash \ kmp就十分简单了。

例题2： [SDOI2017]硬币游戏

把上一题扩展一下，就可以做这道题了。

我们用 \(F_k[i]\) 表示第 \(k\) 个人走 \(i\) 步结束(即胜利)的概率， \(G[i]\) 表示走 \(i\) 步还未结束的概率， \(F_k(x)\) 与 \(G(x)\) 为它们的 \(\mathbf{PGF}\) ，不难发现下面两个等式：

\[\begin{aligned} &\sum_{i}F_i(1)=1\\ &G(x)+\sum_{i}F_i(x)=xG(x)+1 \end{aligned}\]

第一个等式是因为必然会结束，第二个是例题1的等式扩展到多个串的情况。我们要求的即为 \(F_i(1)\) 。考虑在 \(G[i]\) 后面加一个串强制令其结束，设加的是第 \(i\) 个串。

\[G(x)\times(\frac12x)^L=\sum_{j}\sum_{A_i[1:k]=A_j[L-k+1,L]}F_j(x)\times(\frac12x)^{L-k} \]

令 \(x=1\) 得到：

\[G(1)=\sum_{j}\sum_{A_i[1:k]=A_j[L-k+1,L]}F_j(1)\times 2^k \]

在结合第一个等式，我们就可以列出 \(n+1\) 个方程，恰好有 \(n+1\) 个未知数。高斯消元即可。

生成函数&卷积进阶

一些讨论整理在这里。

\(\exp\) 的组合意义

众所周知 \(\exp x\) 是 \(\sum\limits_{i=0}^\infty\dfrac{x^i}{i!}\) ，那么 \(\exp F(x)\) 会得到什么呢？
先暴力展开在说：

\[\exp F(x)=\sum_{i=0}^\infty\frac{F^i(x)}{i!} \]

这个东西是有组合意义的。假如 \(F(x)\) 是“单个元素”的 \(\mathbf{EGF}\) ,那么 \(\exp F(x)\) 就是把这些元素拼接起来的 \(\mathbf{EGF}\)

展开式就相当于枚举有几个元素，多次卷积拼接，由于元素之间无序需要除以个数的阶乘。

例题1：[集训队作业2013]城市规划

如果我们用 \(F[i]\) 表示 \(i\) 个点组成的连通图个数，\(G[i]\) 表示 \(i\) 个点组成的 图 的个数，\(F(x)\) 与 \(G(x)\) 分别为它们的 \(\mathbf{EGF}\)

可以认为是若干个 连通图 组成了一张图，因此可以有：\(\exp F(x)=G(x)\)

于是 \(F(x)=\ln G(x)\) 。 \(G(x)\) 是很好求的，因为 \(G[i]=2^{\tbinom{i}{2}}\)

例题2：有标号荒漠计数

• 先来考虑仙人掌怎么做

本来是无根的，我们强制令其有根。因为有标号，有根方案数除以节点数就是无根方案数。

用 \(F(x)\) 表示方案数的 \(\mathbf{EGF}\)

那么我们先钦定一个点为根，那么这个点可以这样连边：

情况一	情况二	情况三	...
			...
\(F(x)\)	\(\frac{F(x)^2}{2}\)	\(\frac{F(x)^3}{2}\)	...

除以 \(2\) 是因为顺时针与逆时针是一种方案。这部分的生成函数就是 \(\displaystyle F(x)+\frac12\sum_{i=2}F(x)^i\)。

这只是根上的一个基本单位，可以由任意个组成，不难写出方程：

\[F(x)=x\exp(F(x)+\frac12\sum_{i=2}^\infty F(x)^i) \]

后面一串是一个等比数列求和。拆开来就变成 \(\exp\frac{2F(x)-F(x)^2}{2-2F(x)}\)

熟不熟悉？

对 \(F(x)\) 的 \(x^i\) 除以 \(i\) 就得到无根有标号仙人掌的数目了。以下的 \(F(x)\) 指无根。

那么现在荒漠的 \(\mathbf{EGF}\) 就是 \(\exp F(x)\) 了

差/和卷积

在实际卷题的过程中，我们的卷积形式可能不是很明显，比如下边这个柿子：\(H[j]=\sum_{i=j}^nF[i]\times G[i-j]\)

但是这个东西也是可以求的，我们只需要翻转 \(F\) 得到 \(F_R\) ,在翻转 \(H\) 得到 \(H_R\),就可以得到显然的卷积式: \(H_R[n-j]=\sum_{i=j}^nF_R[n-i]\times G[i-j]\) ,这个式子就可以直接卷了。

同样还有类似的和卷积，思路还是翻转形成卷积。

\[H[j]=\sum_{i=0}F[i]\times G[i+j] \]

我们翻转 \(F\) 得到 \(F_R\) ,并把 \(H\) 整体 \(n\) 右移可以得到：

\[H[n+j]=\sum_{i=0}F_R[n-i]\times G[i+j] \]

实战中常常会用到类似的套路。

Bluestein's algorithm

Bluestein's algorithm 算法可以在 \(\Theta(n\log n)\)的时间内完成任意长度的 \(\mathbb{DFT}\)

具体来说是这样的：

\[\begin{aligned} y_k&=\sum_{i=0}^{n-1}a_i\omega_n^{ki}\\ &=\sum_{i=0}^{n-1}a_i\omega_{2n}^{-(k-i)^2 +k^2+i^2}\\ &=\omega_{2n}^{k^2}\sum_{i=0}^{n-1}a_i \omega_{2n}^{i^2}\times\omega_{2n}^{-(k-i)^2} \end{aligned} \]

可以理解为拆指数形成卷积形式。但有些毒瘤题目中可能会不保证 \(\omega_{2n}\) 存在，因此下面介绍另一种常用方法：

\[\begin{aligned} y_k&=\sum_{i=0}^{n-1}a_i\omega_n^{ki}\\ &=\sum_{i=0}^{n-1}a_i\omega_n^{\binom{k+i}{2}-\binom{i}{2}-\binom{k}{2}}\\ &=\omega_{n}^{-\binom{k}{2}}\sum_{i=0}^{n-1}a_i\omega_n^{-\binom{i}{2}}\times\omega_n^{\binom{k+i}{2}} \end{aligned} \]

这个形式显然可以卷积了。可以参见上文的 差/和卷积。

单位根反演

有公式

\[[n|k]=\frac1n\sum_{i=0}^{n-1}\omega_n^{ik} \]

证明直接分类讨论即可：

• \(n|k\) ，\(\omega_n^{ik}=1\) ,上式显然等于 \(1\)
• \(n\not | k\)，等比数列求和得到：\(\dfrac{1}{n}\times \dfrac{\omega_n^{nk}-\omega_n^0}{\omega_n^k-1}=0\)

可以直接记结论。

例题1：小猪佩奇学数学

给定 \(n,p,k\) 询问 \(\sum_{i=0}^n \binom n i \times p^{i} \times \left\lfloor \frac{i}{k} \right\rfloor \bmod 998244353\)

\(k\in\{2^{w}|0\leq w\leq20\}\)就是在保证单位根的存在。

然后就爆推式子。

向下取整可以拆成容易算的 \(\lfloor\frac{i}{k} \rfloor=\frac{i-i \bmod k}{k}\)

原式就可以写成 \(\frac{1}{k}(\sum_{i=0}^n\tbinom{n}{i}p^ii-\sum_{i=0}^n\tbinom{n}{i}p^i(i\bmod k))\)

分开来看式子。

由于组合数的定义： \(\tbinom{n}{i}i=\frac{n!}{i!(n-i)!}i=\frac{n(n-1)!}{(i-1)!(n-i)!}=\tbinom{n-1}{i-1}n\)

\[\begin{aligned} &\sum_{i=0}^n\tbinom{n}{i}p^ii\\ &=\sum_{i=1}^n\tbinom{n-1}{i-1}np^i\\ &=np\sum_{i=0}^{n-1}\tbinom{n-1}{i}p^{i}\\ &=np(p+1)^{n-1} \end{aligned} \]

\[\begin{aligned} &\sum_{i=0}^n\sum_{t=0}^{k-1}[i\bmod k=t]\tbinom{n}{i}p^it\\ &=\sum_{i=0}^n\sum_{t=0}^{k-1}[k|(i-t)]\tbinom{n}{i}p^it\\ &=\sum_{i=0}^n\sum_{t=0}^{k-1}\frac{1}{k}\sum_{j=0}^{k-1}\omega_k^{j(i-t)}\tbinom{n}{i}p^it\\ &=\frac{1}{k}\sum_{j=0}^{k-1}\sum_{t=0}^{k-1}t\omega_k^{-tj}\sum_{i=0}^n\tbinom{n}{i}(\omega_k^jp)^i\\ &=\frac{1}{k}\sum_{j=0}^{k-1}\sum_{t=0}^{k-1}t\omega_k^{-tj}(\omega_k^jp+1)^n \end{aligned} \]

所以只需要对于\(j\in[0,k)\)求出后面一串的值就行了。可以使用Bluestein's Algorithm拆指数具体过程就不展开了。

最后能得到：

\[\frac{1}{k}\sum_{j=0}^{k-1}\omega_k^\tbinom{j}{2}(\omega_k^jp+1)^n\sum_{t=0}^{k-1}t\omega_k^{\tbinom{t}{2}}\times \omega_k^{-\tbinom{t+j}{2}} \]

这就可以卷积了。不过注意 \(\omega_k^{-\tbinom{t+j}{2}}\) 的数组要倍长。

例题2：[HNOI2019]白兔之舞

与上一题类似的操作，不过涉及一点点矩阵。

记\(g_{i,j}\)为走了\(i\)步到第二维为\(j\)的顶点（不钦定走那些列）的方案数，有：

\[g_{i,j}=\sum_{k=1}^ng_{i-1,k}w_{k,j} \]

若记 \(G_i=(g_{i,1},g_{i,2},\ldots,g_{i,n})\)$

\[G_0=(\underbrace{0,\ldots,0}_{x-1},1,\underbrace{0,\ldots,0}_{n-x}) \]

\[S= \begin{pmatrix} w_{1,1}&\cdots&w_{1,n}\\ \vdots&\ddots&\vdots\\ w_{n,1}&\cdots&w_{n,n} \end{pmatrix} \]

有：\(G_i=G_{i-1}\times S\)，即\(G_i=G_0\times S^i\)

但此时我们没有考虑白兔兔每次走了几步。所以我们还需要考虑\(i\)步走了那些列。实际上就是在\(L\)个位置上选了\(i\)个位置唱跳，也就是\(\tbinom{L}{i}g_{i,j}=\tbinom{L}i(G_0S^i)_{1,y}\)

那么此时我们已经表示出跳了\(i\)的方案数。来考虑答案，列出式子开始乱推：

\[\begin{aligned} ans_t&=\sum_{i=0}^L[i\bmod k=t]\tbinom{L}{i}g_{i,y}=\sum_{i=0}^L[k|(i-t)]\tbinom{L}{i}g_{i,y}\\ &=\sum_{i=0}^L\frac{1}{k}\tbinom{L}{i}g_{i,y}\sum_{j=0}^{k-1}\omega_{k}^{(i-t)j}=\frac{1}{k}\sum_{i=0}^L\tbinom{L}{i}g_{i,y}\sum_{j=0}^{k-1}\omega_{k}^{ij}\omega_{k}^{-tj}\\ &=\frac{1}{k}\sum_{j=0}^{k-1}\omega_{k}^{-tj}\sum_{i=0}^L\tbinom{L}{i}g_{i,y}\omega_{k}^{ij}\\ &=\frac{1}{k}\sum_{j=0}^{k-1}\omega_{k}^{-tj}\sum_{i=0}^L\tbinom{L}{i}\omega_{k}^{ij}\times(G_0S^i)_{1,y} \end{aligned} \]

矩阵那部分事实上也可以先提取公因式再求和再取下标，即：

\[\begin{aligned} &=\frac{1}{k}\sum_{j=0}^{k-1}\omega_{k}^{-tj}(G_0\sum_{i=0}^L\tbinom{L}{i}\omega_{k}^{ij}\times S^i)_{1,y}\\ &=\frac{1}{k}\sum_{j=0}^{k-1}\omega_{k}^{-tj}(G_0\sum_{i=0}^L\tbinom{L}{i}(\omega_{k}^{j}\times S)^i)_{1,y}\\ &=\frac{1}{k}\sum_{j=0}^{k-1}\omega_{k}^{-tj}(G_0\sum_{i=0}^L\tbinom{L}{i}(\omega_{k}^{j}\times S)^iI^{L-i})_{1,y}\\ &=\frac{1}{k}\sum_{j=0}^{k-1}\omega_{k}^{-tj}(G_0(\omega_k^jS+I)^L)_{1,y} \end{aligned} \]

如果我们记\(f_i=(G_0(\omega_k^iS+I)^L)_{1,y}\)，就可以吧答案写成比较简单的形式。

\[ans_t=\frac{1}{k}\sum_{j=0}^{k-1}\omega_{k}^{-tj}f_j \]

然后就是 有手就行 的Bluestein's algorithm了。

\[\begin{aligned} ans_t&=\frac{1}{k}\sum_{j=0}^{k-1}\omega_{k}^{-\tbinom{t+j}{2}+\tbinom{t}{2}+\tbinom{j}{2}}f_j\\ &=\frac{\omega_{k}^\tbinom{t}{2}}{k}\sum_{j=0}^{k-1}\omega_{k}^{-\tbinom{t+j}{2}}\times \omega_{k}^\tbinom{j}{2}f_j \end{aligned} \]

卷积就不难了。

二项式反演

有时做题中恰好等词不是怎么好做，我们使用二项式反演可以由至少得到他。（这个至少其实是假的，如果真正意义上的至少只需要差分就行了

\[F[n]=\sum_{i=0}(-1)^i\binom{n}{i}G[i]\Longleftrightarrow G[n]=\sum_{i=0}(-1)^i\dbinom{n}{i}F[i] \]

以及另两种常用的形式

\[F[n]=\sum_{i=0}\binom{n}{i}G[i] \Longleftrightarrow G[n]=\sum_{i=0}^n(-1)^{n-i}\binom{n}{i}F[i] \]

\[F[n]=\sum_{i=n}\binom{i}{n}G[i] \Longleftrightarrow G[n]=\sum_{i=n}(-1)^{i-n}\binom{i}{n}F[i] \]

例题1：[HAOI2018]染色

设 \(G[k]\) 表示有 \(k\) 种颜色恰好出现了 \(S\) 次

那么我们尝试先钦定 \(k\) 种颜色，并强行令其出现恰好 \(S\) 次，我们记做 \(F[k]\) ,不难有：

\[F[k]=\binom{m}{k}\frac{n!}{(S!)^k(n-kS)!}(m-k)^{n-kS} \]

考虑这么算对于一个恰好为 \(i\) 个情况，会计算\(\binom{i}{k}\) 遍，因为同样是恰好 \(i\) 个，钦定的 \(k\) 个不同会重复计算。

于是：

\[F[n]=\sum_{i=n}\binom{i}{n}G[i] \Longleftrightarrow G[n]=\sum_{i=n}(-1)^{i-n}\binom{i}{n}F[i] \]

这个东西也可以卷，拆开组合数就十分明显了QwQ。

\[\begin{aligned} G[n]&=\sum_{i=n}(-1)^{i-n}\frac{i!}{n!(i-n)!}F[i]\\ &=\frac{1}{n!}\sum_{i=n} i!F[i] \frac{(-1)^{i-n}}{(i-n)!} \end{aligned} \]

可以参见 差/和卷积

例题2：[CTS2019]珍珠

记颜色\(c\)有\(cnt_c\)个，一种方案合法当且仅当：\(\sum_{i=1}^Dcnt_i\bmod 2\le m\)

简单推导得到：\(\sum_{i=1}^Dcnt_i\bmod 2\le n-2m\)。注意两种情况需要特判。

记恰好有\(k\)个为奇数方案为\(G[k]\)，至少有\(k\)个为奇数的方案为\(F[k]\)。

\[F[n]=\sum_{i=n}\binom{i}{n}G[i] \Longleftrightarrow G[n]=\frac{1}{n!}\sum_{i=n} i!F[i] \frac{(-1)^{i-n}}{(i-n)!} \]

\(\text{方案的生成函数=选k个生成函数}\times\text{强制奇数生成函数}\times{放任自流生成函数}\)

\[\begin{aligned} F[k]=&\tbinom{D}{k}n(e^x)^{D-k}\\ =&\tbinom{D}{k}\frac{n!}{2^k}[x^n]\sum_{j=0}^k \tbinom{k}{j}(-1)^{k-j}e^{x(D-2(k-j))} \end{aligned}\]

\(e^{ax}=1+\frac{ax}{1!}+\frac{a^2x^2}{2!}+\frac{a^3x^3}{3!}+\ldots\)，即 \(e^{ax}\) 为 \(\mathbb{EGF}<1,a,a^2,a^3,\dots>\) ， \([x^n]e^{ax}=\frac{a^n}{n!}\)

\[\begin{aligned} =&\tbinom{D}{k}\frac{1}{2^k}\sum_{j=0}^k \tbinom{k}{j}(-1)^{k-j}(D-2(k-j))^n\\ =&\frac{D!}{(D-k)!2^k}\sum_{j=0}^k \frac{(-1)^j(D-2j)^n}{j!}\times\frac{1}{(k-j)!}\\ \end{aligned}\]

\(\ln\) 、 \(\exp\) 优化无限背包

在 \(\mathbf{OGF}\) 的例题中我们已经知道可以用其求背包的方案数，就是各部分的 \(\mathbf{OGF}\) 的积。在选无限个的情况下，我们可以通过 \(\ln\) 把求集变成求和，再用 \(\exp\) 还原。

通常有下面的形式：

\[\ln(\frac{1}{1-x^i})=\sum_{j=1}^\infty \frac{x^{ij}}{j} \]

证明：
\(\ln \frac{1}{1-x_i}=-\ln(1-x_i)\)

对右式求导得到：\((-\ln(1-x_i))^\prime=\frac{ix^{i-1}}{1-x^i}\)

我们知道：\(\frac{1}{1-x^i}\)就是\(1+x_i+x^{2i}+\ldots\)的封闭形式，即\(\sum_{j=0}^{+\infty}x^{ij}\)

带回，有：\(\frac{ix^{i-1}}{1-x^i}=\sum_{j=0}^{+\infty}ix^{i(j+1)-1}=\sum_{j=1}^{+\infty}ix^{ij-1}\)

那么

\[\ln\frac{1}{1-x^i}=\int \sum_{j=1}^{+\infty}ix^{ij-1} dx=\sum_{j=1}^{+\infty}\frac{x_{ij}}{j} \]

例题1:付公主的背包

对于体积为 \(V\) 的物品，其生成函数为 \(1+x^V+x^{2V}+\ldots=\frac{1}{1-x^V}\) 。

于是答案的生成函数 \(F(x)\) 就是所有乘起来。

\[F(x)=\prod_i\frac{1}{1-x^{V_i}} \]

两边同取 \(\ln\) 就能去掉乘积了。

\[\ln F(x)=\sum_i\ln\left(\frac{1}{1-x^{V_i}}\right) \]

在用刚刚的式子。

\[\ln F(x)=\sum_i\sum_{j=1}^\infty \frac{x^{V_ij}}{j} \]

我们只需要前 \(n\) 项。如果我们记 \(V_i=k\) 的次数为 \(cnt_k\) ，那么：

\[\ln F(x)=\sum_i\sum_{j=1}^\infty \frac{cnt_ix^{ij}}{j} \]

这个可以用调和级数 \(\Theta(n\ln n)\) 填系数。

例题2：[SDOI2017] 遗忘的集合

首先考虑 \(a_i\in\{0,1\}\) 表示第 \(i\) 个数选还是不选，不难发现第 \(i\) 个数的 \(\mathbf{OGF}\) 就为 \(1+a_i(x^i+x^{2i}+x^{3i}+\ldots)\) ，封闭形式为 \((\frac{1}{1-x^i})^{a_i}\)

随便推导一下得到：

\[\ln F(x)=\sum_{i=1}a_i\sum_{j=1}\frac{x^{ij}}{j} \]

做过莫反的都知道，可以设\(T=ij\)

\[\ln F(x)= \sum_{T=1}(\sum_{i|T}a^i\times\frac iT)x^T\]

\[T[x^T]\ln F(x)=\sum_{i|T}a_i\times i \]

中间的狄利克雷卷积已经很明显了。设两个数论函数 \(f(T)=T[x^T]\ln F(x)\)，\(g(T)=a_T\times T\) ，那么： \(f=g * I\)
两边同乘 \(\mu\) 得到：

\[f*\mu=g*I*\mu=g*(I*\mu)=g*\varepsilon=g \]

\(\Theta(n\ln n)\)求\(f*\mu\)即可