题解 CF414E 【Mashmokh's Designed Problem】
题意
给定一棵 \(n\) 个节点的有根树,每个点连出的边都有序,共有 \(m\) 个操作。操作分三类:
- 查询两个点 \(u,v\) 的距离
- 以 \(v\) 为根的子树从树中分开,并添加一条与其第 \(h\) 个祖先的连边作为该祖先的最后一个儿子。
- 查询从一个点出发,按边的顺序进行dfs,深度为 \(k\) 的最后遍历的点
\((n \le 10^5,m \le 10^5)\)
题解
如果只有 \(1\)、\(2\) 似乎可以 \(\mathbb{LCT}\) 做,但边有顺序无疑让其无法实现。
树的遍历想到欧拉序 (别问我怎么想到的),通过欧拉序,边就都有序了,于是可以完成以上的操作。
记节点 \(i\) 在欧拉序中第一遍为 \(in[i]\) ,第二遍为 \(out[i]\)
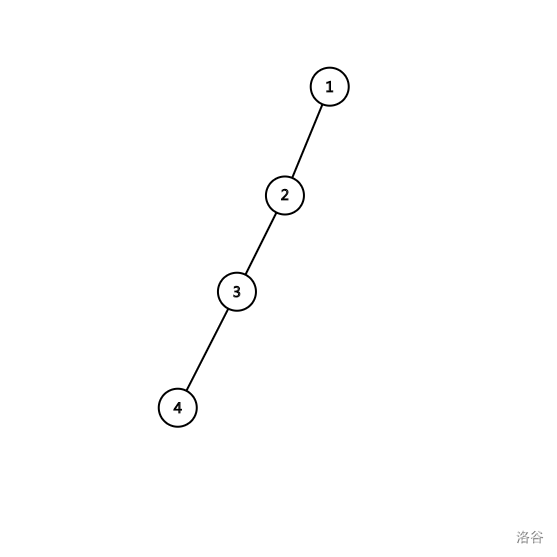
欧拉序:\(1\ 2\ 3\ 4\ 4\ 3\ 2\ 1\)
操作一
如果我们记节点 \(i\) 的深度为 \(dep_i\),那么 \(u\to v\) 的距离就是 \(dep_u+dep_v-2\times dep_{lca(u,v)}\)
假如我们已经能够维护 \(u,v\) 的深度那么考虑 \(\rm lca\) 的深度与欧拉序有什么关系。
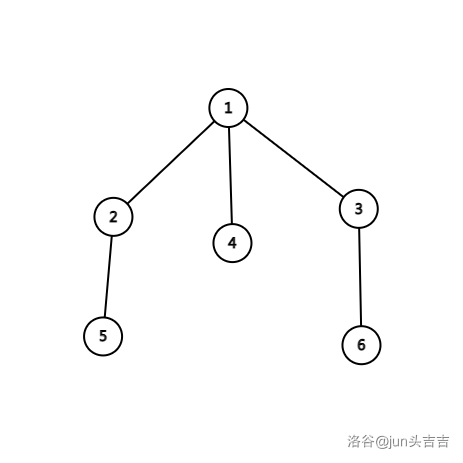
如果我们查\(5\to3\)的\(\rm lca\)
欧拉序:\(\color{black}1\ 2\ 5\ \color{red}5\ 2\ 4\ 4\ 3\ 6\ \color{black}3\ 1\)
发现在 \((in[u],out[v])\) 之间的所有点全在他们的 \(\rm lca\) 以下,取这一段深度的最小值加一即可。
不过注意此时 \(u\) 比 \(v\) 先访问,如果不满足就强行swap(u,v)
取最小值操作我们可以用 \(\rm Splay\)实现。(别问我为什么不用线段树,因为还有其他操作(
操作二
用欧拉序我们可以轻松摘下一棵树再挂上去:
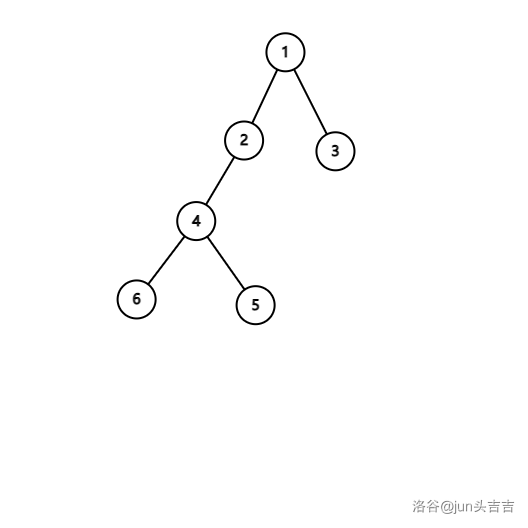
欧拉序:\(\color{black}1\ 2\ \color{red}4\ 6\ 6\ 5\ 5\ 4\ \color{black}2\ 3\ 3\ 1\)
把 \(4\) 的子树摘下来挂到 \(1\) 上
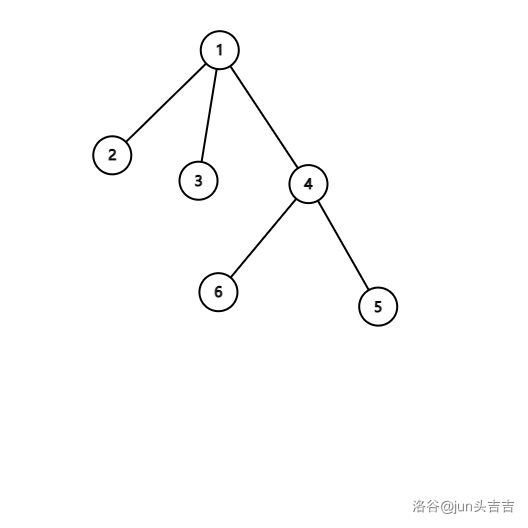
欧拉序: \(\color{black}1\ 2\ 2\ 3\ 3\ \color{blue}4\ 6\ 6\ 5\ 5\ 4\ \color{black}1\)
不难发现把 \(v\) 挂到 \(u\) 上就是把 \([in[v],out[v]]\) 这段区间插到 \(out[u]\) 之前,并把其深度都减少 \(h-1\)
现在大量的序列操作, \(\rm Splay\) 序列之王的用处就体现出来了。
于是现在的问题变为怎么找到 \(u\) ,其实就是 \([1,in[v])\)中最后一个深度为 \(dep[v]-h\) 的点,于是自然引入了操作3
操作三
对于一个深度为 \(k\) 的节点,如果他排列在最后,那么他在欧拉序中的出现也一定在最后。
那么我们对每个节点维护最大值 \(mx\) 与最小值 \(mn\) ,并优先访问右儿子(如果\(k\in [mn_l,mx_l]\)),再是当前节点、左儿子。
那么现在用 \(\mathcal{O}(\log n)\) 的时间,就可以找到最后一个深度为 \(k\) 的了。那么在 操作二寻找指定深度的节点也可以迎刃而解了。
\(\rm Splay\)维护序列这里就不细讲了,做几个模板就都会了。
代码
#include<bits/stdc++.h>
//#define faster
namespace fin{
#ifdef faster
char buf[1<<21],*p1=buf,*p2=buf;
inline int getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
#else
inline int getc(){return getchar();}
#endif
template <typename T>inline void read(T& t){
t=0;int f=0;char ch=getc();while (!isdigit(ch)){if(ch=='-')f = 1;ch=getc();}
while(isdigit(ch)){t=t*10+ch-48;ch = getc();}if(f)t=-t;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){read(t);read(args...);}
}
namespace fout{
char buffer[1<<21];int p1=-1;const int p2 = (1<<21)-1;
inline void flush(){fwrite(buffer,1,p1+1,stdout),p1=-1;}
inline void putc(const char &x) {if(p1==p2)flush();buffer[++p1]=x;}
template <typename T>void write(T x) {
static char buf[15];static int len=-1;if(x>=0){do{buf[++len]=x%10+48,x/=10;}while (x);}else{putc('-');do {buf[++len]=-(x%10)+48,x/=10;}while(x);}
while (len>=0)putc(buf[len]),--len;
}
}
using namespace std;
const int N=2e5+10;
int n,m,in[N],out[N],id[N],dep[N],cnt;
vector<int>e[N];int root;
void dfs(int u,int dep){
in[u]=++cnt,id[cnt]=u,::dep[cnt]=dep;
for(auto v:e[u])dfs(v,dep+1);
out[u]=++cnt,id[cnt]=u,::dep[cnt]=dep;
}
int f[N],ch[N][2],mn[N],mx[N],tag[N],sz[N];
#define min3(a,b,c) min((a),min(b,c))
#define max3(a,b,c) max((a),max(b,c))
void pushup(int x){
int l=ch[x][0],r=ch[x][1];
sz[x]=sz[l]+1+sz[r];
mx[x]=max3(mx[l],dep[x],mx[r]);
mn[x]=min3(mn[l],dep[x],mn[r]);
}
void add(int x,int val){
mn[x]+=val,mx[x]+=val,tag[x]+=val,dep[x]+=val;
}
void pushdown(int x){
int l=ch[x][0],r=ch[x][1];
if(tag[x]){
if(l)add(l,tag[x]);
if(r)add(r,tag[x]);
}tag[x]=0;
}
#define get(x) (ch[f[(x)]][1]==(x))
#define connect(x,y,p) {if(x)f[(x)]=(y);if(y)ch[(y)][(p)]=(x);}
void rotate(int x){
int fa=f[x],ffa=f[fa],p1=get(x),p2=get(fa);
connect(ch[x][p1^1],fa,p1);
connect(fa,x,p1^1);
connect(x,ffa,p2);
pushup(fa);pushup(x);
}
void splay(int x,int goal=0){
stack<int>q;q.push(x);
for(int fa=x;f[fa]!=goal;fa=f[fa])q.push(f[fa]);
while(q.size())pushdown(q.top()),q.pop();
for(int fa;(fa=f[x])!=goal;rotate(x))
if(f[fa]!=goal)rotate(get(x)==get(fa)?fa:x);
if(!goal)root=x;
}
#define mid (l+r>>1)
int build(int l,int r){
if(l<mid)ch[mid][0]=build(l,mid-1),f[ch[mid][0]]=mid;
if(mid<r)ch[mid][1]=build(mid+1,r),f[ch[mid][1]]=mid;
pushup(mid);return mid;
}
int findk(int x,int k){
int l=ch[x][0],r=ch[x][1];pushdown(x);
if(mn[r]<=k&&k<=mx[r])return findk(r,k);
else if(dep[x]==k){splay(x);return id[x];}
else return findk(l,k);
}
int split(int l,int r){
splay(l);splay(r,l);return ch[r][0];
}
int getpre(int x){
splay(x);x=ch[x][0];
while(ch[x][1])x=ch[x][1];
splay(x);return x;
}
int getsuf(int x){
splay(x);x=ch[x][1];
while(ch[x][0])x=ch[x][0];
splay(x);return x;
}
int del(int l,int r){
int L=getpre(l),R=getsuf(r);
int x=split(L,R),y=f[x];
ch[y][0]=f[x]=0;pushup(y);pushup(f[y]);
return x;
}
signed main(){
fin::read(n,m);
for(int i=1,u,v;i<=n;i++){
fin::read(u);
for(int j=1;j<=u;j++)fin::read(v),e[i].push_back(v);
}
mn[0]=0x3f3f3f3f;
dfs(1,0);build(1,cnt);
while(m--){
int op,u,v,k;
fin::read(op);
if(op==1){
fin::read(u,v);
splay(in[u]);int rku=sz[ch[in[u]][0]]+1,res=dep[in[u]];
splay(in[v]);int rkv=sz[ch[in[v]][0]]+1;res+=dep[in[v]];
if(rku>rkv)swap(u,v);u=split(in[u],out[v]);res-=(mn[u]-1)*2;
fout::write(res);fout::putc('\n');
}else if(op==2){
fin::read(u,v);int val=v-1;
splay(in[u]);v=findk(ch[in[u]][0],dep[in[u]]-v);
u=del(in[u],out[u]);add(u,-val);
int rt=getpre(out[v]);splay(rt);
splay(out[v],rt);
connect(u,out[v],0);
pushup(out[v]),pushup(rt);
}else{
fin::read(k);
splay(1);
fout::write(findk(1,k));fout::putc('\n');
}
}
fout::flush();
return 0;
}

