题解 CF575I 【Robots protection】

题意

进行 \(q\) 次操作，每次操作有两种，要么放置一个等腰直角三角形，要么查询某一个点被多少个三角形覆盖。

每个等腰直角三角形可以用四个参数 \(dir,x,y,len\) 确定，其中 \(dir \in [1,4]\) 表示三角形的方向，\((x,y)\) 表示直角的顶点坐标，\(len\) 表示直角边的长度。

\(x,y\in [1,n]\)

\(n≤5×10^3,q\le 10^5\)

题解

成功抢到最劣解

如果想当做思维题做，那么请不要看这篇题解。

以下为套路解法。

我们先考虑方向往右上的三角形，就是下面一种：

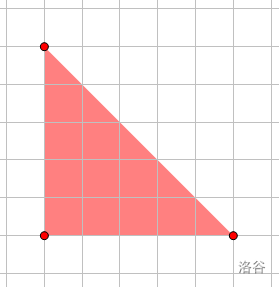
如果顶点为\((a,b)\)，边长为\(r\)，那么它上面一条直线的解析式显然为\(y=-x+a+b+r\)

那么一个点\(x,y\)在三角形内，则必然有：

\[\begin{cases}a\le x\\ b\le y\\ a+b+r≥ x+y\end{cases} \]

那如果在加入一个时间戳\(t\)，就变成了

\[\begin{cases}t_1\le t_2\\ a\le x\\ b\le y\\ a+b+r≥ x+y\end{cases} \]

此时就变成一个简单的四位偏序，但是\(\mathcal{O}(n\times\log^3n)\)不太可过的样子，于是可以用一些奇奇怪怪的方法降低常数。

于是我们考虑合并\([l,mid]\)与\([mid+1,r]\)两个区间，那么区间内部的贡献已经统计完了，那么对于\(a\in [mid+1,r]\)，就是在\([l,mid]\)找到第一个\(x_b>x_a\)，在\([1,b)\) 中计算

\[\begin{cases}y\le y_a \\ x+y+r≥x_a+y_a\end{cases}\]

由于\(y\le 5000,x+y+r\le 5000\times 2\)直接上树状数组统计即可。

现在我们已经统计完了一种方向的答案，那么剩下三种的答案。当然可以重新讨论，但我们可以通过旋转变成上面的形式。

于是最劣解就被口胡出来了

复杂度：\(\mathcal{O}(n\times\log_2n\times\log_25000\times\log_210000)\)

丑陋的代码

#include<bits/stdc++.h>
//#define fast
namespace in{
	#ifdef fast
	char buf[1<<21],*p1=buf,*p2=buf;
	inline int getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
	#else
	inline int getc(){return getchar();}
	#endif
	template <typename T>inline void read(T& t){
		t=0;int f=0;char ch=getc();while (!isdigit(ch)){if(ch=='-')f = 1;ch=getc();}
	    while(isdigit(ch)){t=t*10+ch-48;ch = getc();}if(f)t=-t;
	}
	template <typename T,typename... Args> inline void read(T& t, Args&... args){read(t);read(args...);}
}
namespace out{
	char buffer[1<<21];int p1=-1;const int p2 = (1<<21)-1;
	inline void flush(){fwrite(buffer,1,p1+1,stdout),p1=-1;}
	inline void putc(const char &x) {if(p1==p2)flush();buffer[++p1]=x;}
	template <typename T>void write(T x) {
		static char buf[15];static int len=-1;if(x>=0){do{buf[++len]=x%10+48,x/=10;}while (x);}else{putc('-');do {buf[++len]=-(x%10)+48,x/=10;}while(x);}
		while (len>=0)putc(buf[len]),--len;
	}
}
using namespace std;
const int N=5e3+1;
int lowbit(int x){return x&-x;}
struct TREE{
	int tree[N*2+1];
	void ins(int x){
		for(int i=x;i<=2*N;i+=lowbit(i))
			tree[i]++;
	}
	void clear(int x){
		for(int i=x;i<=2*N;i+=lowbit(i))
			tree[i]=0;
	}
	int qry(int x){
		int res=0;
		for(int i=x;i;i-=lowbit(i))
			res+=tree[i];
		return res;
	}
	int val(int x){
		return qry(2*N)-qry(x-1);
	}
};
TREE tree[N+1];
void upd(int x,int val){
	for(int i=x;i<=N;i+=lowbit(i))
		tree[i].ins(val);
}
int qry(int x,int val){
	int res=0;
	for(int i=x;i;i-=lowbit(i))
		res+=tree[i].val(val);
	return res;
}
void clear(int x,int val){
	for(int i=x;i<N;i+=lowbit(i))
		tree[i].clear(val);
}
const int Q=1e5+100;
int n,q,ans[Q];
int op[Q],dir[Q],x[Q],y[Q],r[Q];
namespace CDQ{
	struct node{
		int op;
		int id;
		int x,y,r;
	}a[Q];
	int cnt=0;
	#define mid (l+r>>1)
	void cdq(int l,int r){
		//printf("%d %d\n",l,r);
		if(l>=r)return;
		cdq(l,mid);cdq(mid+1,r);
		sort(&a[l],&a[mid+1],[&](node a,node b){return a.x!=b.x?a.x<b.x:(a.y!=b.y?a.y<b.y:a.op<b.op);});
		sort(&a[mid+1],&a[r+1],[&](node a,node b){return a.x!=b.x?a.x<b.x:(a.y!=b.y?a.y<b.y:a.op<b.op);});
		int now=l;//下一个选的
		for(int i=mid+1;i<=r;i++)
			if(a[i].op==2){
				//统计跨块的贡献
				while(now<=mid&&a[now].x<=a[i].x){
					if(a[now].op==2){now++;continue;}
					upd(a[now].y,a[now].x+a[now].y+a[now].r);now++;
				}
				ans[a[i].id]+=qry(a[i].y,a[i].x+a[i].y);
			} 
		for(int i=l;i<now;i++)
			clear(a[i].y,a[i].x+a[i].y+a[i].r);
	}
	void init(){cnt=0;}
	void run(){cdq(1,cnt);}
}
signed main(){
	in::read(n,q);
	for(int i=1;i<=q;i++){
		in::read(op[i]);
		if(op[i]==1)in::read(dir[i],x[i],y[i],r[i]);
		else in::read(x[i],y[i]);
	}
	CDQ::init();
	for(int i=1;i<=q;i++)
		if(op[i]==1&&dir[i]==1)CDQ::a[++CDQ::cnt]=(CDQ::node){1,i,x[i],y[i],r[i]};
		else if(op[i]==2)      CDQ::a[++CDQ::cnt]=(CDQ::node){2,i,x[i],y[i],r[i]};
	CDQ::run();
	CDQ::init();
	for(int i=1;i<=q;i++)
		if(op[i]==1&&dir[i]==2)CDQ::a[++CDQ::cnt]=(CDQ::node){1,i,N-y[i],x[i],r[i]};
		else if(op[i]==2)      CDQ::a[++CDQ::cnt]=(CDQ::node){2,i,N-y[i],x[i],r[i]};
	CDQ::run();
	CDQ::init();
	for(int i=1;i<=q;i++)
		if(op[i]==1&&dir[i]==4)CDQ::a[++CDQ::cnt]=(CDQ::node){1,i,N-x[i],N-y[i],r[i]};
		else if(op[i]==2)      CDQ::a[++CDQ::cnt]=(CDQ::node){2,i,N-x[i],N-y[i],r[i]};
	CDQ::run();
	CDQ::init();
	for(int i=1;i<=q;i++)
		if(op[i]==1&&dir[i]==3)CDQ::a[++CDQ::cnt]=(CDQ::node){1,i,y[i],N-x[i],r[i]};
		else if(op[i]==2)      CDQ::a[++CDQ::cnt]=(CDQ::node){2,i,y[i],N-x[i],r[i]};
	CDQ::run();
	
	for(int i=1;i<=q;i++)
		if(op[i]==2)out::write(ans[i]),out::putc('\n');
	out::flush();
	return 0;
}