图形结构及其算法
1. 图介绍
2. 图的数据表示法
3. 图的遍历
4. 最小成本生成树
5. 图的最短路径法
1. 图介绍
(本文中“图”和“图形”在数据结构的描述中指同一个概念。在图论中,图的定义有特定的含义。)
图在实际的应用场景中经常出现,比如交通中的线路图等。图还被应用在数据结构中的最短路径搜索、拓扑排序等。
例如,如何计算网络上两个节点之间最短距离的问题,就变成图的数据结构要处理的问题,采用 Dijkstra 这种图形算法就能快速寻找出两个节点之间的最短距离,如果没有 Dijkstra 算法,现代网络的运行效率必将大大降低。
图的定义
图(Graph)是由“顶点”和“边”所组成的集合,顶点(vertex)通常用圆圈来表示,边(edge)就是这些圆圈之间的连线,还可以根据顶点之间的关系为边设置不同的权重,默认权重相同(皆为 1)。
此外,根据边的方向性,还可将图分为有向图和无向图。
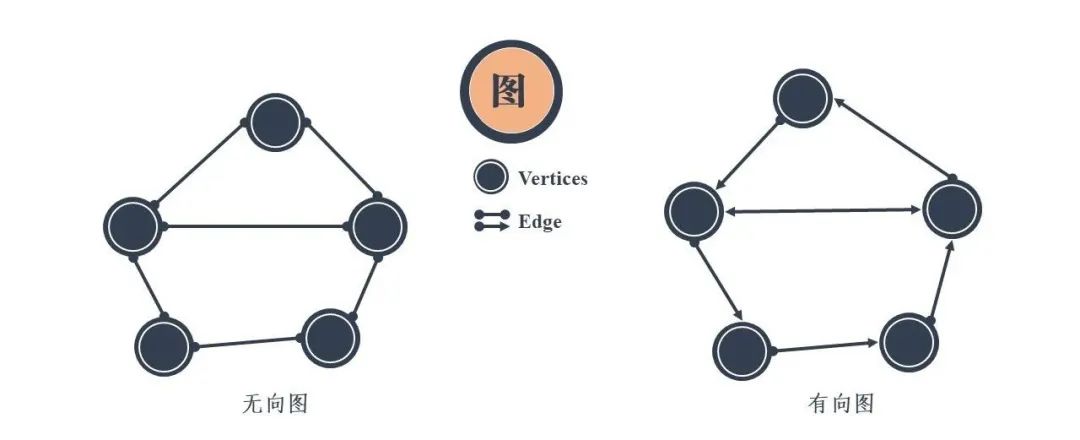
和树比起来,图是一种更加复杂的非线性表结构。树描述的是节点与节点之间“层次”的关系,而图却是讨论两个顶点之间“连通与否”的关系。
图的相关概念及应用示例
微信
- 比如在微信中可以把每个用户看作一个顶点。
- 如果两个用户之间互加好友,那就在两者之间建立一条边。
- 所以,整个微信的好友关系就可以用一张图来表示。其中,每个用户有多少个好友,对应到图中,就叫作顶点的度(degree),就是跟顶点相连接的边的条数。
微博
- 微博的社交关系跟微信有点不一样,或者说更加复杂一点。微博允许单向关注,也就是说,用户 A 关注了用户 B,但用户 B 可以不关注用户 A。
- 因此,可以把图结构稍微改造一下,引入边的“方向”的概念:
- 如果用户 A 关注了用户 B,就在图中画一条从 A 到 B 的带箭头的边,来表示边的方向。
- 如果用户 A 和用户 B 互相关注了,那就画一条从 A 指向 B 的边,再画一条从 B 指向 A 的边。
- 我们把这种边有方向的图叫作“有向图”(Digraph)。以此类推,把边没有方向的图叫作“无向图”(Graph)。
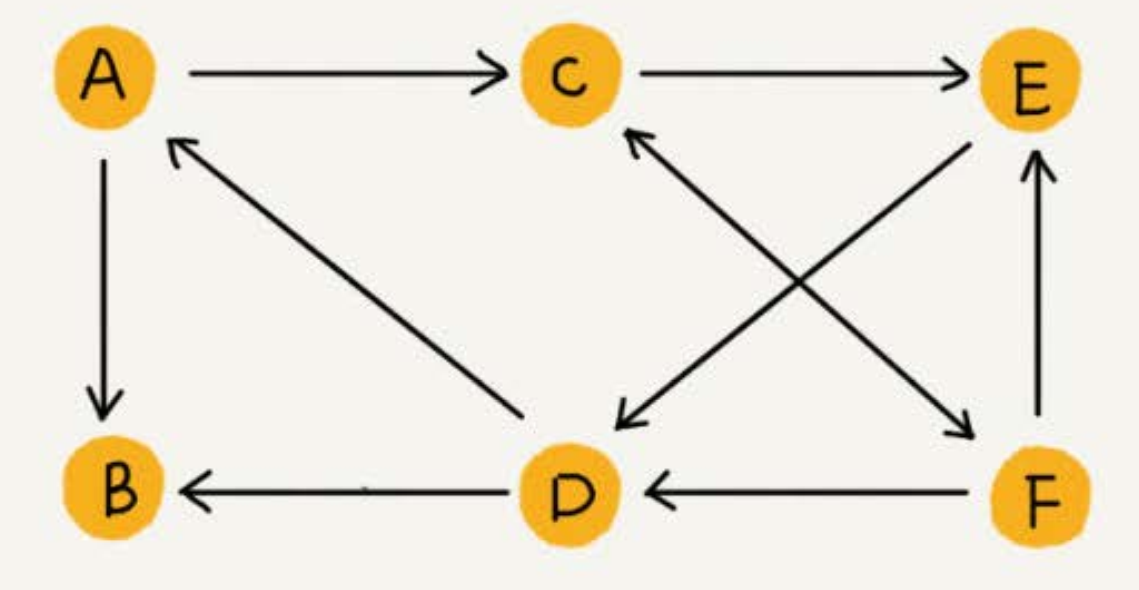
- 无向图中有“度”这个概念,表示一个顶点有多少条边;而在有向图中,把度分为入度(In-degree)和出度(Out-degree)。
- 顶点的入度:表示有多少条边指向这个顶点。
- 顶点的出度:表示有多少条边是以这个顶点为起点指向其他顶点。
- 对应到微博的例子,入度就表示有多少粉丝,出度就表示关注了多少人。
- QQ 中的社交关系要更复杂一点。QQ 不仅记录了用户之间的好友关系,还记录了两个用户之间的亲密度。如果两个用户经常往来,那亲密度就比较高;如果不经常往来,亲密度就比较低。
- 为此,要用到另一种图——带权图(weighted graph)。在带权图中,每条边都有一个权重(weight),可以通过这个权重来表示 QQ 好友间的亲密度。

2. 图的数据表示法
图结构用抽象的图线来表示十分简单,顶点和边之间的关系非常清晰明了。但是在具体的代码实现中,为了将各个顶点和边的关系存储下来,却不是一件易事。
1)邻接矩阵
图最直观的一种存储方法就是邻接矩阵(Adjacency Matrix),邻接矩阵的底层依赖一个二维数组。
对于一个图 G = (V, E),V 代表顶点的集合,E 代表边的集合。假设该图有 n 个顶点, n >= 1,则可以将 n 个顶点使用一个 n X n 的二维矩阵来表示。其中若 A(i, j) = 1,则表示图中有一条边 (Vi, Vj) 存在;反之,若 A(i, j) = 0,则不存在 (Vi, Vj)。
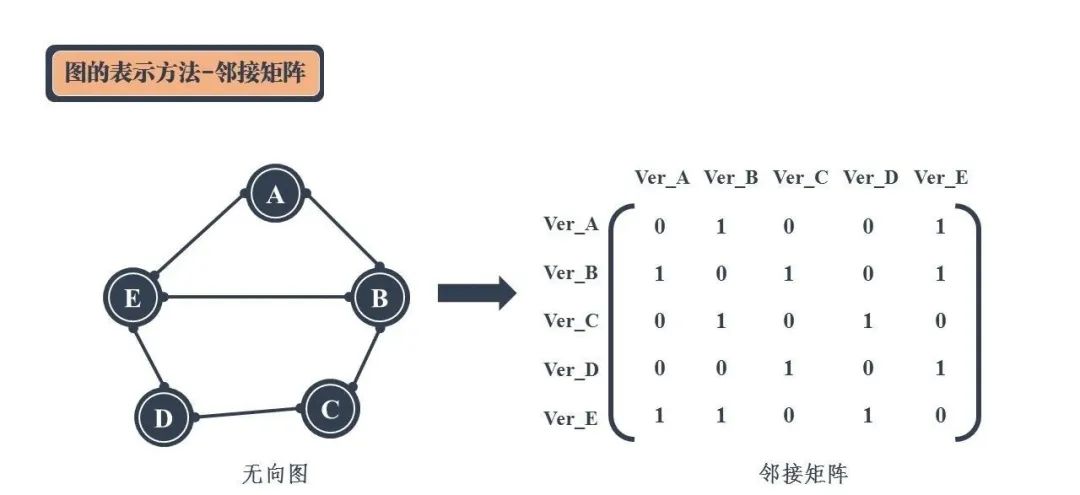
-
对无向图而言,如果顶点 i 与顶点 j 之间有边,就将 A[i][j] 和 A[j][i] 标记为 1;
-
对有向图而言,如果顶点 i 到顶点 j 之间有一条箭头从顶点 i 指向顶点 j 的边,那就将 A[i][j] 标记为 1。
-
对带权图而言,数组中就存储相应的权重。
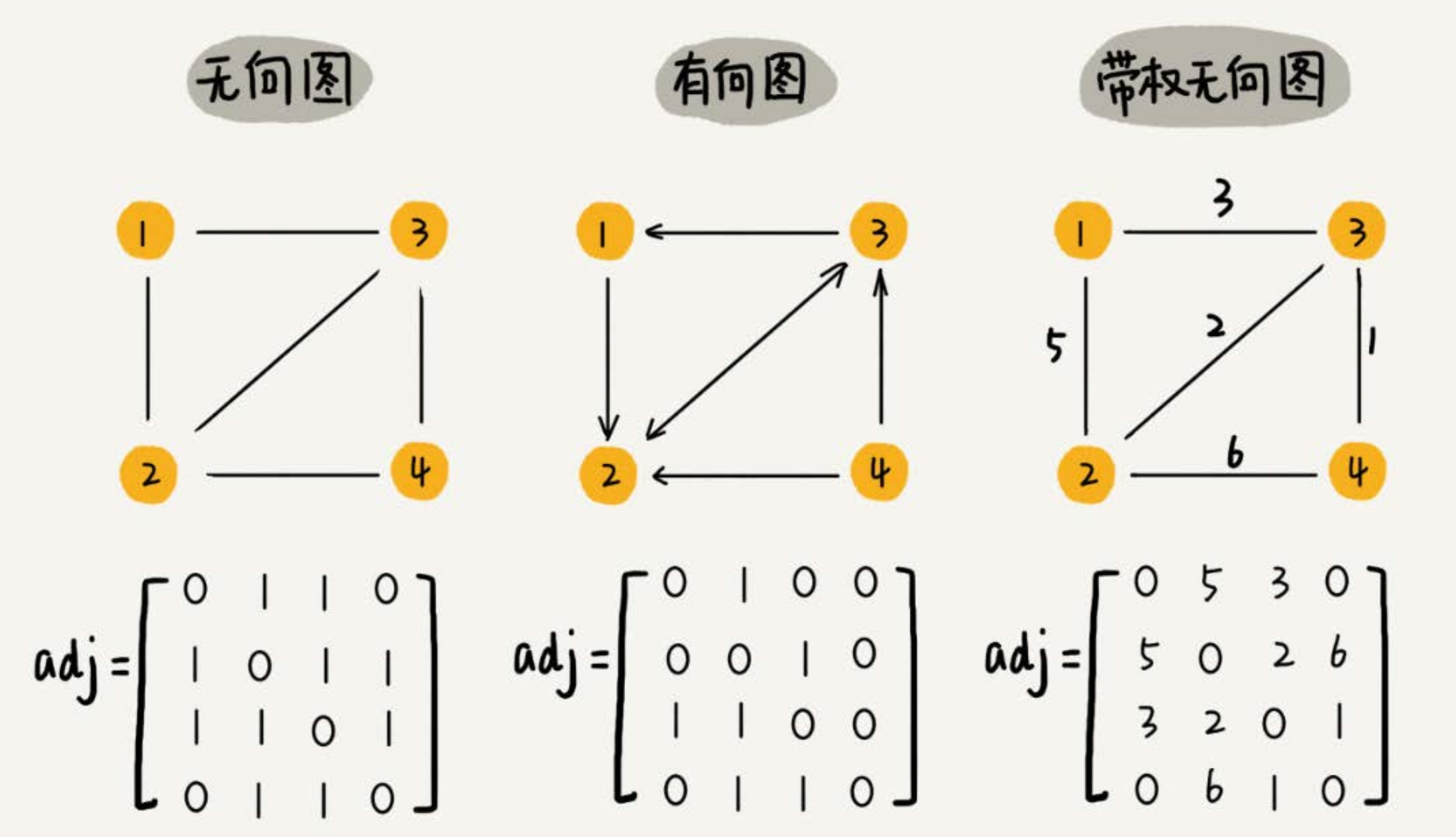
相关特性说明
-
对无向图而言,邻接矩阵一定是对称的,而且对角线一定为 0;有向图则不一定如此。
- 对无向图而言,顶点 i 的度就是第 i 行所有元素的和;而在有向图中,顶点 i 的出度就是第 i 行所有元素的和,而入度是第 j 列所有元素的和。
- 用邻接矩阵表示图共需要 n2 个单位空间,由于无向图的邻接矩阵一定具有对称关系的,扣除对角线全部为零之外,仅需存储上三角形或下三角形的数据即可,因此仅需 n(n-1)/2 的单位空间。
邻接矩阵的优缺点
优点
- 邻接矩阵的存储方式简单直观,因为基于数组,所以在获取两个顶点的关系时,就非常高效。
- 要在图中加入新边时,这个表示法的插入和删除操作相当简易。
- 用邻接矩阵存储图的另外一个好处是计算方便,借着矩阵的运算有许多特别的应用。
缺点
用邻接矩阵来表示一个图,虽然简单、直观,但是比较浪费存储空间。如果要计算所有顶点的度,其时间复杂度为 O(n2)。
- 无向图的二维数组中,如果将其用对角线划分为上下两部分,只需要利用上面或者下面这样一半的空间就足够了,另外一半白白浪费掉了。
- 如果存储的是稀疏图(Sparse Matrix),也就是说,顶点很多但每个顶点的边并不多,那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户,对应到图上就是好几亿个顶点,但是每个用户的好友并不会很多,一般也就三五百个而已。如果用邻接矩阵来存储,那绝大部分的存储空间都被浪费了。
代码实现邻接矩阵
1 # 无向图的邻接矩阵算法 2 def adjacency_matrix(arr): 3 # 首先获取最大顶点值,即 n*n的n 4 max_n = 1 5 for e in arr: 6 if e[0] > max_n: 7 max_n = e[0] 8 if e[1] > max_n: 9 max_n = e[1] 10 # 矩阵中的行和列的索引默认从1开始,所以长度要+1 11 n = max_n + 1 12 # 初始化结果矩阵(n*n) 13 result_arr = [[0]*n for row in range(n)] 14 15 # 读取图的每条边的数据,获取起始和终止顶点 16 for i in range(len(arr)): 17 tmp_i = arr[i][0] # 起始顶点 18 tmp_j = arr[i][1] # 终止顶点 19 result_arr[tmp_i][tmp_j] = 1 # 有边的点填入1 20 21 # 输出结果 22 print("邻接矩阵:") 23 for i in range(1, n): 24 for j in range(1, n): 25 print("%s " % result_arr[i][j], end=" ") 26 print() 27 return result_arr 28 29 30 # 无向图 31 graph_data = [[1,2], [2,1], [1,5], [5,1], [2,3], [3,2], [2,4], [4,2], [3,4], [4,3]] 32 adjacency_matrix(graph_data) 33 34 # 有向图 35 digraph_data = [[1,2], [2,1], [2,3], [2,4], [4,3], [4,1]] 36 adjacency_matrix(digraph_data)
执行结果:
邻接矩阵: 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 0 0 0 邻接矩阵: 0 1 0 0 1 0 1 1 0 0 0 0 1 0 1 0
2)邻接表
针对邻接矩阵较为浪费内存空间的问题,可以考虑更有效的另一种图的存储方法——邻接表(Adjacency List)。邻接表有点像散列表,每个顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。
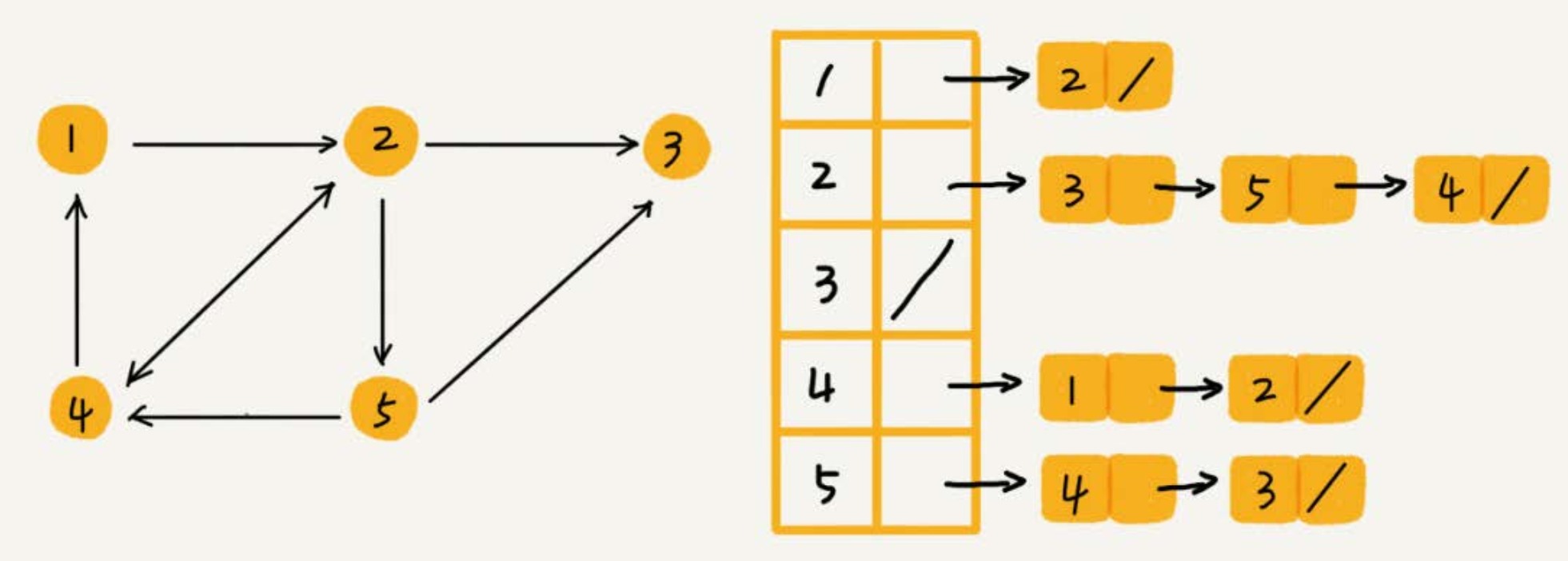
下图中画的是一个有向图的邻接表存储方式,每个顶点对应的链表里面,存储的是指向的顶点。对无向图而言也是类似的,只是每个顶点的链表中存储的,是跟这个顶点有边相连的顶点。
邻接表的优缺点
这其实就是时间、空间复杂度互换的设计思想:邻接矩阵存储起来比较浪费空间,但是使用起来比较节省时间;相反,邻接表存储起来比较节省空间,但是使用起来就较为耗时。
优点
- 邻接矩阵如果要计算所有顶点的度,其时间复杂度为 O(n2);而邻接表计算所有顶点的度,邻接表的时间复杂度为 O(n+e),n 为链表个数,e 为每个链表中的元素个数。
缺点
- 比起邻接矩阵的存储方式,在邻接表中查询两个顶点之间的关系就没那么高效了。如上图示例,如果要确定,是否存在一条从顶点 2 到顶点 4 的边,那就要遍历顶点 2 对应的那条链表,看链表中是否存在顶点 4。
- 有新边加入图中或从图中删除边时,就要修改相关的链表链接,较为麻烦和耗时。
邻接表的优化方案
- 在基于链表法解决冲突的散列表中,如果链过长,为了提高查找效率,可以将链表换成其他更加高效的数据结构,比如平衡二叉查找树等。而因为邻接表长得很像散列表,所以也可以将邻接表同散列表一样进行“改进升级”。
- 例如可以将邻接表中的链表改成平衡二叉查找树,来提高查询效率。实际开发中,可以选择用红黑树。这样,就可以更加快速地查找两个顶点之间是否存在边了。
- 这里的二叉查找树还可以换成其他动态数据结构,比如跳表、散列表等。
- 除此之外,还可以将链表改成有序动态数组,可以通过二分查找的方法来快速定位两个顶点之间否是存在边。
代码实现邻接表
1 # 链表的节点类 2 class Node: 3 4 def __init__(self, data=None): 5 self.data = data 6 self.next = None 7 8 # 链表类 9 class LinkList: 10 11 def __init__(self, data=None): 12 self.root = Node(data) 13 14 def add(self, data): 15 if self.root is None: 16 self.root = Node(data) 17 else: 18 cur = self.root 19 while cur.next is not None: 20 cur = cur.next 21 cur.next = Node(data) 22 23 def travel(self): 24 cur = self.root 25 while cur is not None: 26 print(cur.data, end=" ") 27 cur = cur.next 28 29 # 邻接表算法 30 def adjacency_list(arr): 31 # 邻接表结果 32 result_arr = [] 33 # 遍历图的每个数据,获取起始顶点和终止顶点 34 for e in arr: 35 # 遍历现有链表,如果该起始顶点的链表已存在,则新增节点 36 for cur_link in result_arr: 37 if cur_link.root.data == e[0]: 38 cur_link.add(e[1]) 39 break 40 # 如果不存在,则新增链表 41 else: 42 ll = LinkList(e[0]) 43 ll.add(e[1]) 44 result_arr.append(ll) 45 46 # 打印结果 47 print("邻接表:") 48 for link in result_arr: 49 link.travel() 50 print() 51 return result_arr 52 53 graph_data = [[1,2], [2,1], [2,3], [3,2], [2,4], [4,2], [3,4], [4,3], [2,5], [5,3], [3,5], [5,3], [4,5], [5,4]] 54 adjacency_list(graph_data)
执行结果:
邻接表:
1 2
2 1 3 4 5
3 2 4 5
4 2 3 5
5 3 3 4
3)逆邻接表
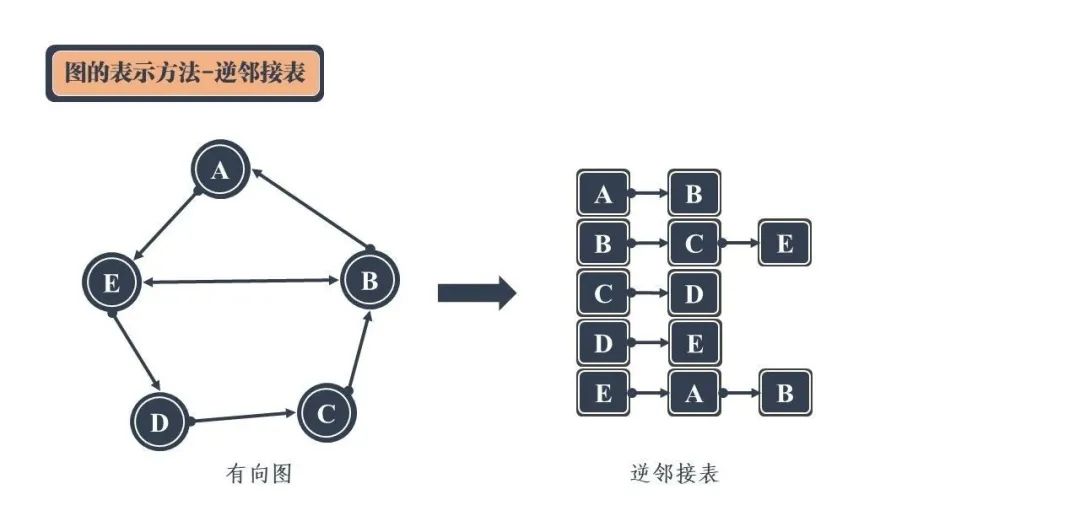
4)十字链表

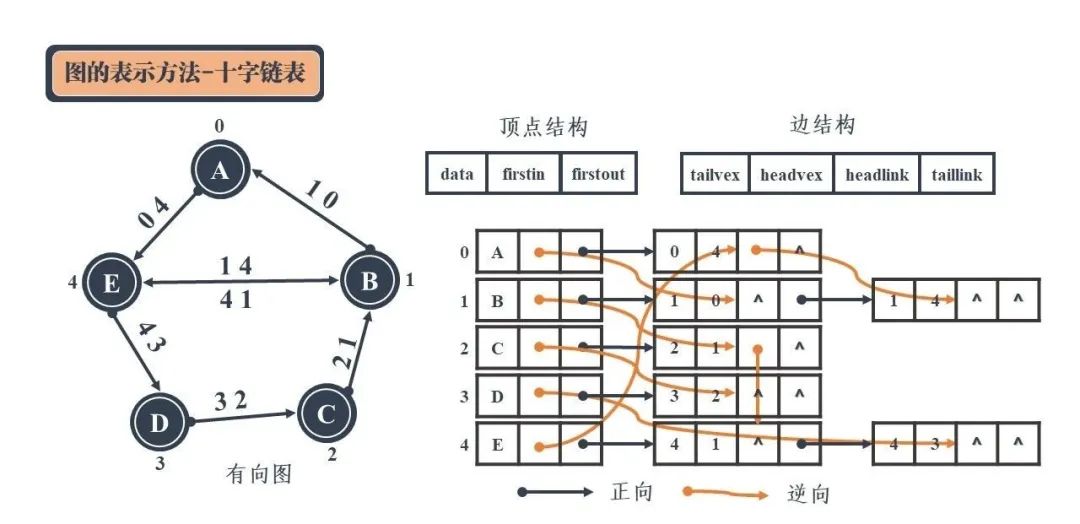
但这并不是最优的表示方式。虽然这样的方式共用了中间的顶点存储空间,但是邻接表和逆邻接表的链表节点中重复出现的顶点并没有得到重复利用,反而是进行了再次存储。因此,上图的表示方式还可以进行进一步优化,如下图所示:
-
data:用于存储该顶点中的数据;
-
firstin 指针:用于连接从别的顶点指进来的顶点;
-
firstout 指针:用于连接从该顶点指出去的顶点。
-
tailvex:用于存储作为弧尾的顶点的编号;
-
headvex:用于存储作为弧头的顶点的编号;
-
headlink 指针:用于链接下一个存储作为弧头的顶点的节点;
-
taillink 指针:用于链接下一个存储作为弧尾的顶点的节点。
以上图为例子,对于顶点 A 而言,其作为起点能够到达顶点 E。因此在邻接表中顶点 A 要通过边 AE(即边 04)指向顶点 E,顶点 A 的 firstout 指针需要指向边 04 的 tailvex。同时,从 B 出发能够到达 A,所以在逆邻接表中顶点 A 要通过边 AB(即边 10)指向 B,顶点 A 的 firstin 指针需要指向边 10 的弧头,即 headlink 指针。依次类推。
应用示例:如何存储微博社交网络中的好友关系
数据结构是为算法服务的,所以具体选择哪种存储方法,与期望支持的操作有关系。针对微博用户关系,假设需要支持下面这样几个操作:
- 判断用户 A 是否关注了用户 B;
- 判断用户 A 是否是用户 B 的粉丝;
- 用户 A 关注用户 B;
- 用户 A 取消关注用户 B;
- 根据用户名称的首字母排序,分页获取用户的粉丝列表;
- 根据用户名称的首字母排序,分页获取用户的关注列表。
1)邻接表
关于如何存储一个图,主要的存储方法有:邻接矩阵和邻接表。而因为社交网络是一张稀疏图,使用邻接矩阵存储比较浪费存储空间。所以,这里采用邻接表来存储。
2)邻接表 + 逆邻接表
不过,用一个邻接表来存储这种有向图是不够的。比如去查找某个用户关注了哪些用户非常容易,但是如果要想知道某个用户都被哪些用户关注了,也就是用户的粉丝列表,是非常困难的。
基于此,需要一个逆邻接表。邻接表中存储了用户的关注关系,逆邻接表中存储的是用户的被关注关系。
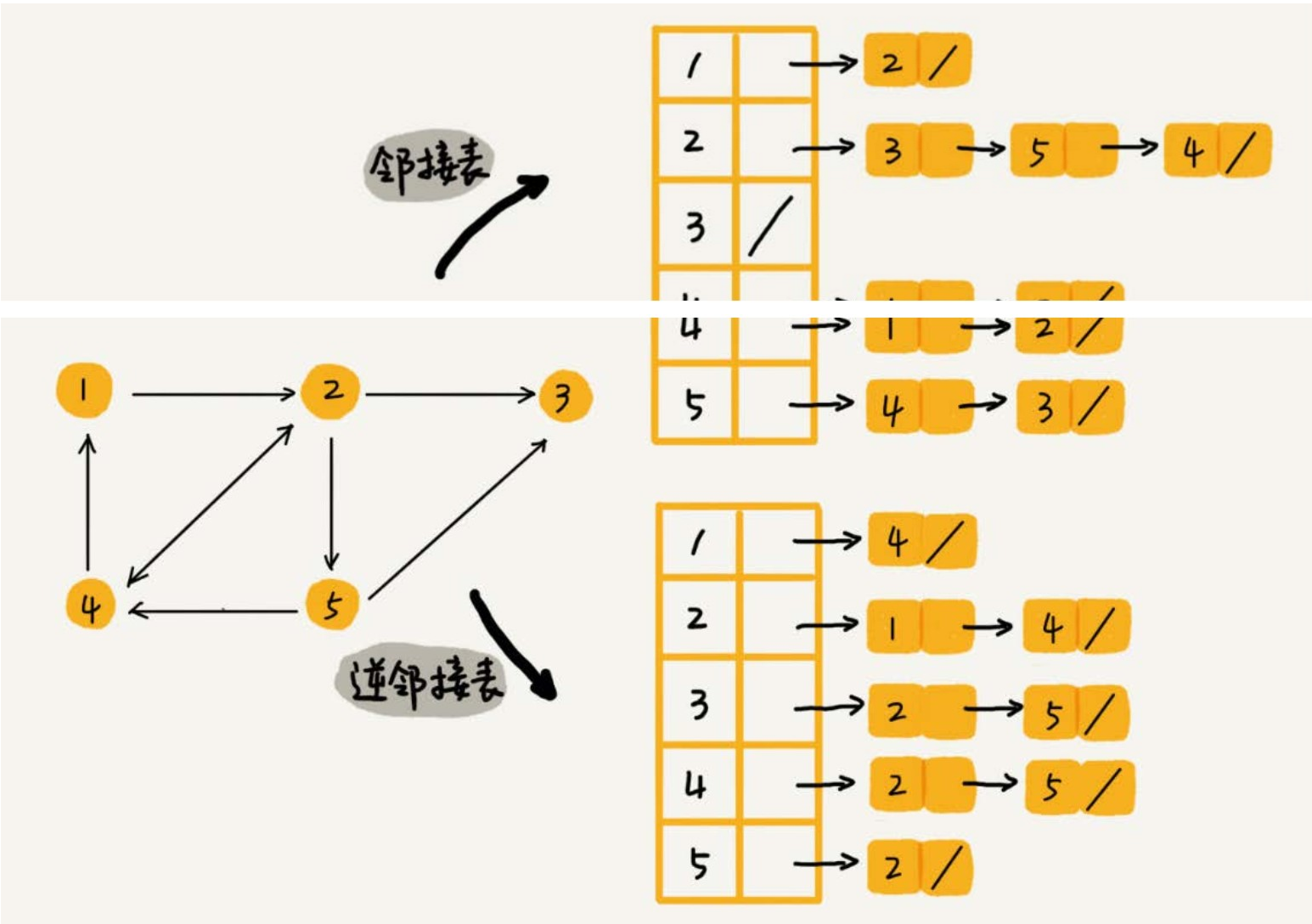
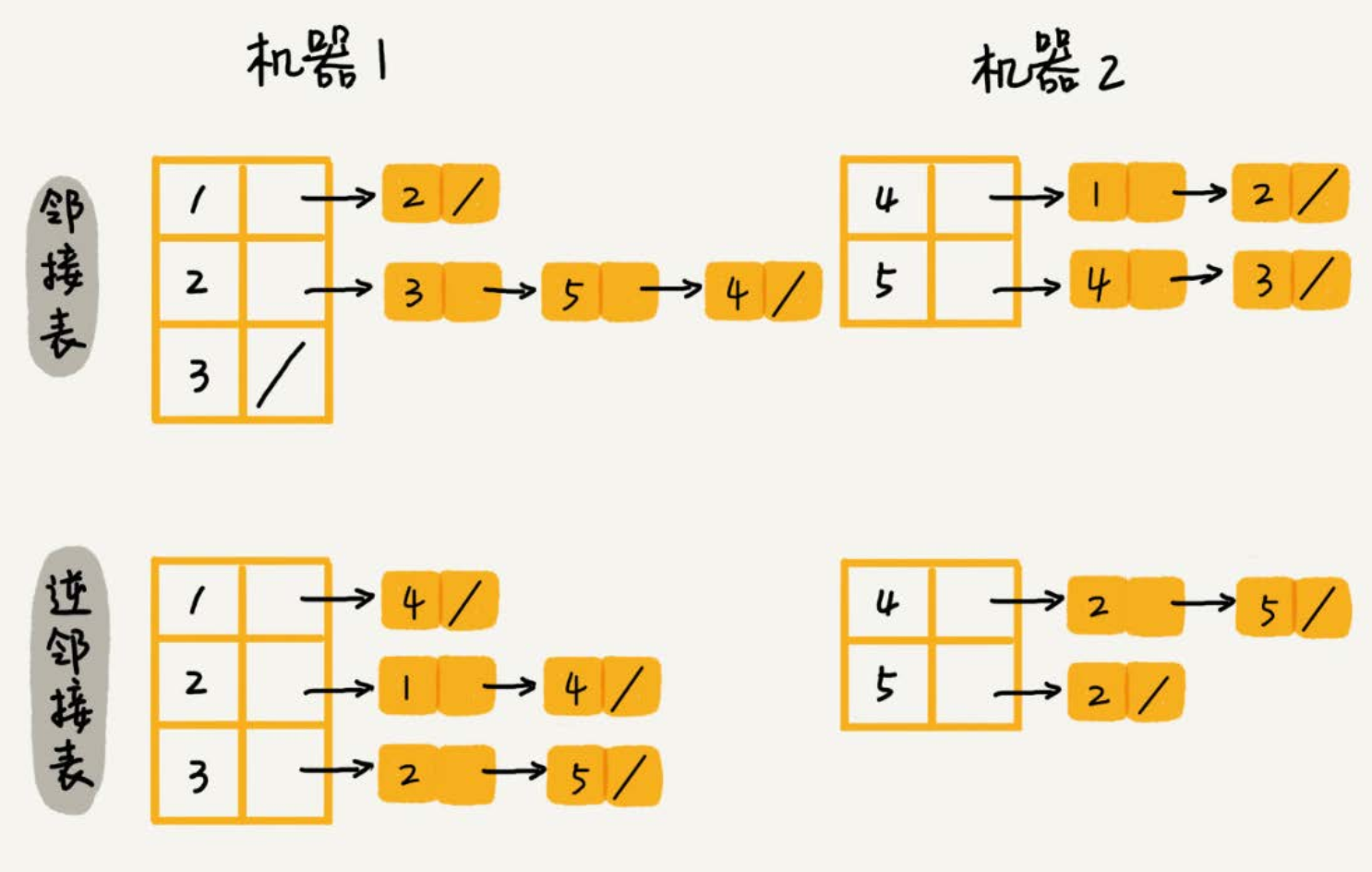
对应到下图,邻接表中,每个顶点的链表中,存储的就是这个顶点指向的顶点;逆邻接表中,每个顶点的链表中,存储的是指向这个顶点的顶点。
如果要查找某个用户关注了哪些用户,可以在邻接表中查找;如果要查找某个用户被哪些用户关注了,从逆邻接表中查找。
3)改进邻接表中的链表 —> 跳表
但基础的邻接表不适合快速判断两个用户之间是否是关注与被关注的关系,所以选择改进版本,将邻接表中的链表改为支持快速查找的动态数据结构。比如:红黑树、跳表、有序动态数组、散列表等。
因为需要按照用户名称的首字母排序,且需要分页来获取用户的粉丝列表或者关注列表,因此这里选择跳表。
跳表的插入、删除、查找都非常高效,时间复杂度是 O(logn),空间复杂度上稍高,是 O(n)。
最重要的一点,跳表中存储的数据本来就是有序的了,分页获取粉丝列表或关注列表,就非常高效。
4)哈希算法
如果对于小规模的数据,比如社交网络中只有几万、几十万个用户,可以将整个社交关系存储在内存中,上面的解决思路是没有问题的。但是如果像微博那样有上亿的用户,数据规模太大,就无法全部存储在内存中了。
可以通过哈希算法等数据分片方式,将邻接表存储在不同的机器上。如下图所示:机器 1 上存储顶点 1、2、3 的邻接表,在机器 2 上,存储顶点 4、5 的邻接表。逆邻接表的处理方式也一样。
当要查询顶点与顶点关系的时候,就利用同样的哈希算法,先定位顶点所在的机器,然后在相应的机器上查找。
5)外部存储 —> 数据库
除此之外,还有另外一种解决思路,就是利用外部存储(比如硬盘),因为外部存储的存储空间要比内存会宽裕很多。
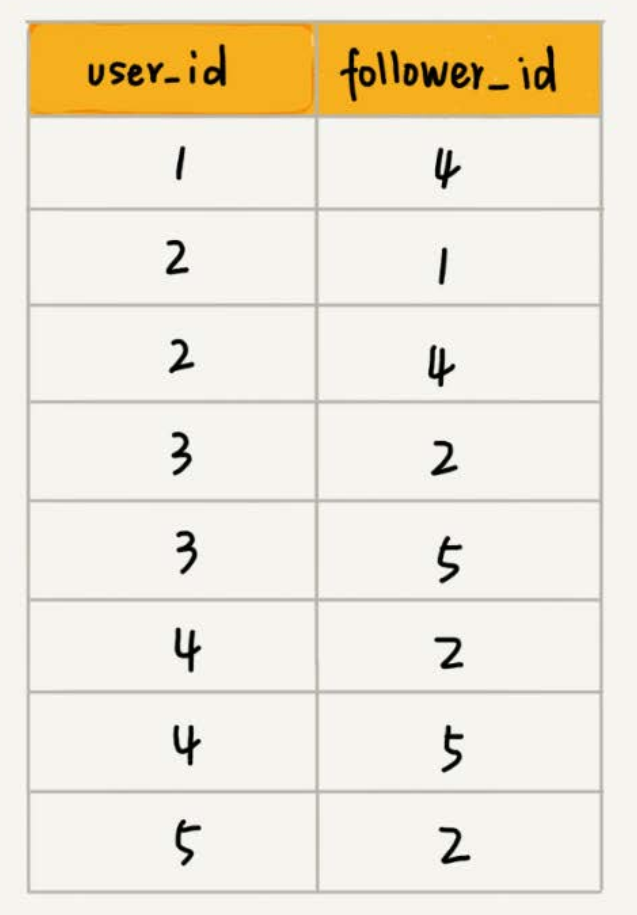
数据库是经常用来持久化存储关系数据的,用下面这张表来存储这样一个图。为了高效地支持前面定义的操作,可以在表上建立多个索引,比如第一列、第二列,给这两列都建立索引。
3. 图的遍历
树的遍历目的是访问每一个节点仅一次,而图的遍历指的是从图中的任一顶点出发,对图中的所有顶点访问一次且仅访问一次。图的遍历是图的一种基本操作,图的许多其它操作都是建立在遍历操作的基础之上。
图的遍历可以划分为两种搜索策略:
- 深度优先遍历/搜索(DFS,Depth First Search)
- 广度优先遍历/搜索(BFS,Breadth First Search)
1)深度优先遍历
深度优先遍历指从图的某一顶点开始遍历,被访问过的顶点就做上已访问的记号,接着遍历此顶点所有相邻且未访问过的顶点中的任一顶点,并做上已访问的记号,再以该点为新的起点继续进行深度优先遍历。
这种图的遍历方法结合了递归和堆栈的技巧,由于此方法会造成无限循环,因此必须加入一个变量,判断该点是否已经遍历完毕。
图解深度优先遍历步骤
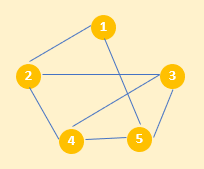
- 以顶点 1 为起点,将相邻的顶点 2 和顶点 5 压入堆栈:[5, 2]
- 弹出顶点 2,将与顶点 2 相邻且未访问过的顶点 3 和顶点 4 压入堆栈:[5, 4, 3]
- 弹出顶点 3,将与顶点 3 相邻且未访问过的顶点 4 和顶点 5 压入堆栈:[5, 4, 5, 4]
- 弹出顶点 4,将与顶点 4 相邻且未访问过的顶点 5 压入堆栈:[5, 4, 5, 5]
- 弹出顶点 5,将与顶点 5 相邻且未访问过的顶点压入堆栈。此时与顶点 5 相邻的顶点都访问过了,所以无需再压栈:[5, 4, 5]
- 将堆栈内的值弹出并判断是否已经遍历过了,直到堆栈内无节点可遍历为止。
故该图的深度优先遍历顺序为:顶点 1、2、3、4、5。
代码实现深度优先遍历
1 # 链表的节点类 2 class Node: 3 4 def __init__(self, data=None): 5 self.data = data 6 self.next = None 7 8 # 链表类 9 class LinkList: 10 11 def __init__(self, data=None): 12 self.root = Node(data) 13 14 def add(self, data): 15 if self.root is None: 16 self.root = Node(data) 17 else: 18 cur = self.root 19 while cur.next is not None: 20 cur = cur.next 21 cur.next = Node(data) 22 23 def travel(self): 24 cur = self.root 25 while cur is not None: 26 print(cur.data, end=" ") 27 cur = cur.next 28 29 # 邻接表算法 30 def adjacency_list(arr): 31 # 邻接表结果 32 result_arr = [] 33 # 遍历图的每个数据,获取起始顶点和终止顶点 34 for e in arr: 35 # 遍历现有链表,如果该起始顶点的链表已存在,则新增节点 36 for cur_link in result_arr: 37 if cur_link.root.data == e[0]: 38 cur_link.add(e[1]) 39 break 40 # 如果不存在,则新增链表 41 else: 42 ll = LinkList(e[0]) 43 ll.add(e[1]) 44 result_arr.append(ll) 45 46 # 打印结果 47 print("邻接表:") 48 for link in result_arr: 49 link.travel() 50 print() 51 print() 52 return result_arr 53 54 55 # 深度遍历算法 56 def dfs(run_list, arr, current): 57 # run_list 记录每个顶点是否被访问过 58 # arr 表示邻接表 59 # current 表示当前所在顶点,1 表示已访问 60 run_list[current] = 1 61 print(arr[current].root.data, end=" ") # 打印顶点 62 cur = arr[current].root.next 63 while cur is not None: # 遍历访问相邻顶点 64 # 如果顶点未被访问过,就递归调用dfs(效果等同压栈) 65 if run_list[cur.data-1] == 0: 66 dfs(run_list, arr, cur.data-1) 67 cur = cur.next 68 69 70 # 原始图数据 71 graph_data = [[1,2], [1,5], [2,1], [2,3], [2,4], [3,2], [3,4], [3,5], [4,2], [4,3], [4,5], [5,1], [5,3], [5,4]] 72 73 # 记录每个顶点是否访问过,0 表示未访问过 74 run = [0] * len(graph_data) 75 76 # 使用邻接表存储原始图数据 77 arr = adjacency_list(graph_data) 78 79 print("深度优先遍历结果:") 80 # 进行深度优先遍历 81 dfs(run, arr, 0)
执行结果:
邻接表: 1 2 5 2 1 3 4 3 2 4 5 4 2 3 5 5 1 3 4 深度优先遍历结果: 1 2 3 4 5
2)广度优先遍历
广度优先遍历利用队列和递归技巧,从图的某一顶点开始遍历,被访问过的顶点就做上已访问的记号,接着遍历此顶点所有相邻且未访问过的顶点中的任一顶点,并做上已访问的记号,再以该点为新的起点继续进行深度优先遍历。
图解广度优先遍历步骤

- 以顶点 1 为起点,将相邻的顶点 2 和顶点 5 加入队列:[2, 5]
- 取出顶点 2,将与顶点 2 相邻且未访问过的顶点 3 和顶点 4 加入队列:[5, 3, 4]
- 取出顶点 5,将与顶点 5 相邻且未访问过的顶点 3 和顶点 4 加入队列:[3, 4, 3, 4]
- 取出顶点 3,将与顶点 3 相邻且未访问过的顶点 4 加入队列:[4, 3, 3, 4]
- 取出顶点 4,将与顶点 4 相邻且未访问过的顶点加入队列。此时与顶点 4 相邻的顶点都访问过了,所以再加入队列:[3, 4, 2, 4]
- 将队列内的值取出并判断是否已经遍历过了,直到队列内无节点可遍历为止。
故该图的广度优先遍历顺序为:顶点 1、2、5、3、4。
代码实现广度优先遍历
1 # 链表的节点类 2 class Node: 3 4 def __init__(self, data=None): 5 self.data = data 6 self.next = None 7 8 # 链表类 9 class LinkList: 10 11 def __init__(self, data=None): 12 self.root = Node(data) 13 14 def add(self, data): 15 if self.root is None: 16 self.root = Node(data) 17 else: 18 cur = self.root 19 while cur.next is not None: 20 cur = cur.next 21 cur.next = Node(data) 22 23 def travel(self): 24 cur = self.root 25 while cur is not None: 26 print(cur.data, end=" ") 27 cur = cur.next 28 29 # 邻接表算法 30 def adjacency_list(arr): 31 # 邻接表结果 32 result_arr = [] 33 # 遍历图的每个数据,获取起始顶点和终止顶点 34 for e in arr: 35 # 遍历现有链表,如果该起始顶点的链表已存在,则新增节点 36 for cur_link in result_arr: 37 if cur_link.root.data == e[0]: 38 cur_link.add(e[1]) 39 break 40 # 如果不存在,则新增链表 41 else: 42 ll = LinkList(e[0]) 43 ll.add(e[1]) 44 result_arr.append(ll) 45 46 # 打印结果 47 print("邻接表:") 48 for link in result_arr: 49 link.travel() 50 print() 51 print() 52 return result_arr 53 54 # 队列类 55 class Queue: 56 57 def __init__(self): 58 self.queue = [] 59 60 def enqueue(self, data): 61 self.queue.append(data) 62 63 def dequeue(self): 64 return self.queue.pop(0) 65 66 def is_empty(self): 67 return len(self.queue) == 0 68 69 70 # 广度遍历算法 71 def bfs(queue, run_list, arr, current): 72 # queue 队列 73 # run_list 记录每个顶点是否被访问过 74 # arr 表示邻接表 75 76 run_list[current] = 1 # current 表示当前所在顶点,1 表示已访问 77 queue.enqueue(arr[current].root.data) # 将第一个顶点加入队列 78 print(arr[current].root.data, end=" ") # 打印第一个顶点的值 79 # 判断当前队列是否为空 80 while not queue.is_empty(): 81 # 取出队列中的顶点 82 cur = queue.dequeue() 83 cur_node = arr[cur-1].root 84 # 遍历访问相邻顶点 85 while cur_node is not None: 86 # 如果顶点未被访问过 87 if run_list[cur_node.data-1] == 0: 88 queue.enqueue(cur_node.data) 89 run_list[cur_node.data-1] = 1 # 记录已遍历过 90 print(cur_node.data, end=" ") # 打印顶点 91 cur_node = cur_node.next 92 93 94 # 原始图数据 95 graph_data = [[1,2], [1,5], [2,1], [2,3], [2,4], [3,2], [3,4], [3,5], [4,2], [4,3], [4,5], [5,1], [5,3], [5,4]] 96 97 # 记录每个顶点是否访问过,0 表示未访问过 98 run = [0] * len(graph_data) 99 100 # 使用邻接表存储原始图数据 101 arr = adjacency_list(graph_data) 102 103 print("广度优先遍历结果:") 104 # 进行广度优先遍历 105 bfs(Queue(), run, arr, 0)
执行结果:
邻接表: 1 2 5 2 1 3 4 3 2 4 5 4 2 3 5 5 1 3 4 广度优先遍历结果: 1 2 5 3 4
4. 最小成本生成树
基本概念
无向连通图
无向图中,如果任意两个顶点之间都能够连通,则称此无向图为连通图。如下图的无向图就是一个连通图,因为此图中任意两顶点之间都是连通的。
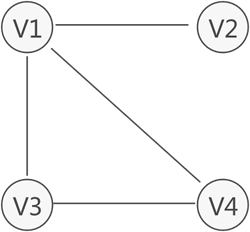
(V2 和 V4 通过 V1 中转连通)
最小生成树
首先对于一张图,我们有一个定理:n 个顶点用 n-1 条边连接,形成的图形只可能是树。我们可以这样理解:树中的每一个节点都有唯一的父节点,也就是至少有 n 条边,但是根节点要除外,所以就是 n-1 条边。
那么,对于一张 n 个顶点的带权的无向连通图,它的生成树(spanning tree)就是用其中的 n-1 条边来连接这 n 个顶点,而最小成本生成树(MST,Minimun Cost Spanning Tree)就是 n-1 条边的边权之和最小的一种方案。简单的理解,就是用让这张图只剩下 n-1 条边,同时这 n-1 条边的边权总和最小。
最小生成树在生活中的应用十分广泛,比如:要连通 n 个城市需要 n-1 条边线路,那么怎么样建设才能使工程造价最小呢?可以把线路的造价看成权值,来求这几个城市的连通图的最小生成树。求最小造价的过程也就转化成求最小生成树的过程,则最小生成树表示使其造价最小的生成树。
常用算法
求最小生成树的过程,我们可以理解为建一棵树。要使边权总和最小,我们不难想到可以用贪心的思想:让最小生成树里的每一条边都尽可能小。那么我们有两种思路,分别对应着两种算法: Kruskal 算法( 克鲁斯卡尔算法)和 Prim 算法(普里姆算法)。Kruskal 算法涉及大量对边的操作,因此适用于稀疏图;普通的 prim 算法则适用于稠密图。
Kruskal 算法( 克鲁斯卡尔算法)
我们不难想到一种贪心的策略:每一条边的边权都是小的,那这些边连接起来的边权总和一定也是小的。因此,我们可以先挑选最小的,再挑选次小的、第三小的......直到我们挑了 n-1 条边。为此,我们可以将这些边按照边权排序,然后开始挑选边。为什么是挑选边呢?不是越小的边越好吗,为什么还要挑?
边权小固然好,但是不要忘记我们有一个大前提:我们要建的是树,它里面不能存在环。也就是说,假如我们看到一条边连着的两个顶点在我们建的树里已经连通了,那这条边还需要再加进来吗?很显然不用。
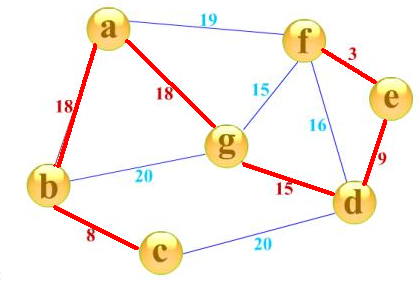
图解用 K 氏法得到最小生成树

我们将上图的边排序后从小到大依次为:
| 起始顶点 | 终止顶点 | 成本/权值 |
| 1 | 2 | 1 |
| 1 | 3 | 2 |
| 4 | 6 | 3 |
| 5 | 6 | 4 |
| 2 | 3 | 6 |
| 4 | 5 | 7 |
| 3 | 4 | 9 |
| 2 | 4 | 11 |
| 3 | 5 | 13 |
要建的最小生成树一开始如下所示:

我们的操作就是往这棵树里加边,其操作过程如下所示:
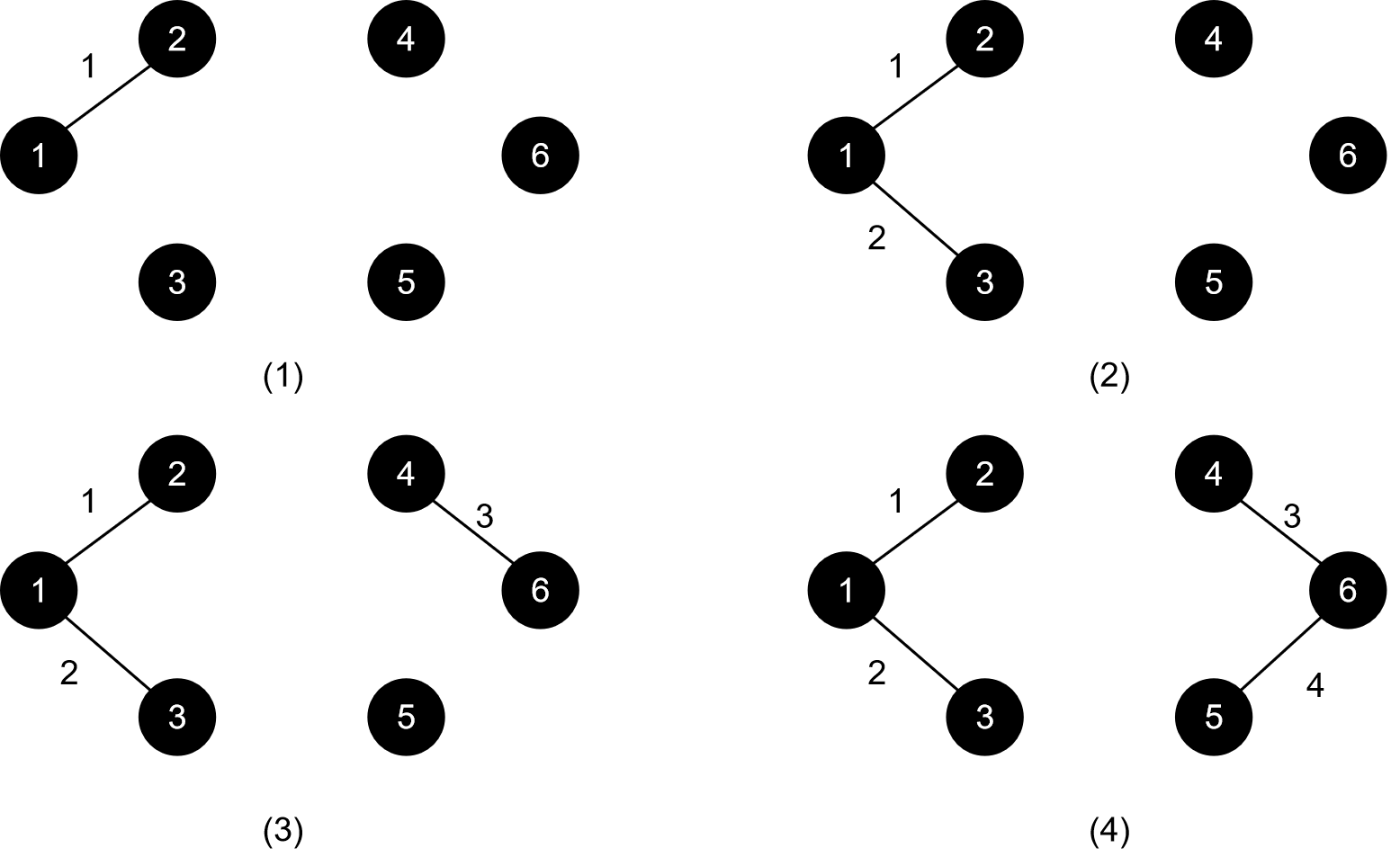

至此,我们建的树里每个节点都已经连接了,刚好用了 5 条边,也就是我们说的 n-1 条边,算法结束。
代码实现 K 氏法
算法的难点在于如何判断两点是否已经连通。我们可以用深搜或广搜来解决,但显然效率极低。因此,我们需要借助一种强大的数据结构:并查集。并查集的最强大的功能就是可以快速地判断两个元素是否在同一集合内(祖先是否相同),所以我们可以借助它来判断两点是否连通。
下面将使用一个二维数组存储成本表并用 K 氏法对其排序,最后求出最小成本树。
1 # 成本表数组 2 data = [[1,2,1], [1,3,2], [2,3,6], [2,4,11], [3,4,9], [3,5,13], [4,6,3], [4,5,7], [5,6,4]] 3 # 图的顶点数 4 VERTS = 6 5 6 7 # 声明边的类 8 class Edge: 9 def __init__(self): 10 self.start = 0 # 起始顶点 11 self.to = 0 # 终止顶点 12 self.find = 0 # 该边是否已加入图 13 self.val = 0 # 权值/成本 14 self.next = None # 链接下一条边 15 16 17 # 建立图的链表(用链表将顶点升序连接) 18 def graph_link(data): 19 head = None 20 for i in range(len(data)): 21 for j in range(1, VERTS+1): 22 # 如果遍历到的成本表数据的起始顶点等于顶点记录表v的索引位(顶点值) 23 if data[i][0] == j: 24 new_node = Edge() 25 new_node.start = data[i][0] 26 new_node.to = data[i][1] 27 new_node.val = data[i][2] 28 new_node.find = 0 29 if head is None: 30 head = new_node 31 else: 32 cur = head 33 while cur.next is not None: 34 cur = cur.next 35 cur.next = new_node 36 return head 37 38 39 # 根据传入的图链表,搜索成本最小的边 40 def find_min_cost(head): 41 min_val = 100 # 初始化一个最小成本 42 cur = head 43 tmp_min_edge = cur 44 while cur is not None: 45 # 如果找到更小成本的边,且改变未被搜索过 46 # 就把改变设为当前最小成本 47 if cur.val < min_val and cur.find == 0: 48 min_val = cur.val 49 tmp_min_edge = cur 50 cur = cur.next 51 tmp_min_edge.find = 1 # 将tmp_min_edge 设为已找到的边 52 return tmp_min_edge 53 54 55 # 自定义并查集类,用来判断两点是否已连通。 56 # 并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。常常在使用中以森林来表示。 57 class UnionFind: 58 59 # 在构造函数中,初始化一个数组parent,parent[i]表示的含义为,索引为i的节点,它的直接父节点为parent[i]。 60 # 初始化时各个节点都不相连,因此初始化parent[i]=i,让自己成为自己的父节点,从而实现各节点不互连。 61 def __init__(self, n): 62 self.parent = list(range(n)) 63 64 # 由于parent[i]仅表示自己的直接父节点,查询两个节点是否相交需要比较它们的根节点是否相同 65 def get_root(self, i): 66 while i != self.parent[i]: # 循环找到根节点 67 i = self.parent[i] 68 return i 69 70 # 通过来比较根节点是否相同来判断两节点是否连通 71 def is_connected(self, i, j): 72 return self.get_root(i) == self.get_root(j) 73 74 # 当要连通两个节点时,我们要将其中一个节点的根节点的parent,设置为另一个节点的根节点。 75 # 注意,连通两个节点并非仅仅让两节点自身相连,实际上是让它们所属的集合实现合并。 76 def union(self, i, j): 77 i_root = self.get_root(i) 78 j_root = self.get_root(j) 79 self.parent[i_root] = j_root 80 81 82 # 最小成本树生成函数 83 def min_tree(head): 84 cur = head 85 u = UnionFind(VERTS+1) 86 # 遍历图链表中的所有边 87 while cur is not None: 88 # 每次从图链表中找出最小成本的边 89 min_edge = find_min_cost(head) 90 # 如果起始和终止顶点已连通,则跳过该边;否则就设为连通 91 if not u.is_connected(min_edge.start, min_edge.to): 92 u.union(min_edge.start, min_edge.to) 93 print("起始顶点 [%d] —> 终止顶点 [%d] —> 成本 [%d]" \ 94 % (min_edge.start, min_edge.to, min_edge.val)) 95 cur = cur.next 96 97 98 print("*"*50) 99 print("建立最小成本树:") 100 print("*"*50) 101 min_tree(graph_link(data))
执行结果:
**************************************************
建立最小成本树:
**************************************************
起始顶点 [1] —> 终止顶点 [2] —> 成本 [1]
起始顶点 [1] —> 终止顶点 [3] —> 成本 [2]
起始顶点 [4] —> 终止顶点 [6] —> 成本 [3]
起始顶点 [5] —> 终止顶点 [6] —> 成本 [4]
起始顶点 [3] —> 终止顶点 [4] —> 成本 [9]
Prim 算法(普里姆算法)
除了通过加入边来建树,我们还有没有其它的方法了呢?Kurskal 中,我们加入边,是在我们固定了节点的情况下完成的。也就是,我们这时候不在乎这些节点,我们只在乎连接它们的边。那我们可以不可以在乎一下这些节点呢?这时候,我们建树的过程就不是添加边了,而是添加点。
Prim 算法的基本思路
将图中的所有的顶点分为两类:树顶点(已经被选入生成树的顶点)和非树顶点(还未被选入生成树的顶点)。
首先选择任意一个顶点加入生成树,接下来要找出一条边添加到生成树,这需要枚举每一个树顶点到每一个非树顶点所有的边,然后找到最短边加入到生成树。依次重复操作 n-1 次,直到将所有顶点都加入生成树中。
图解 Prim 算法
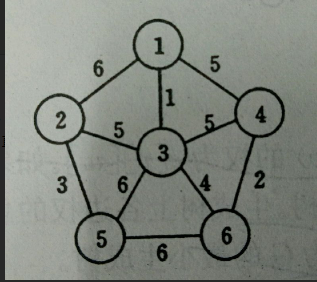
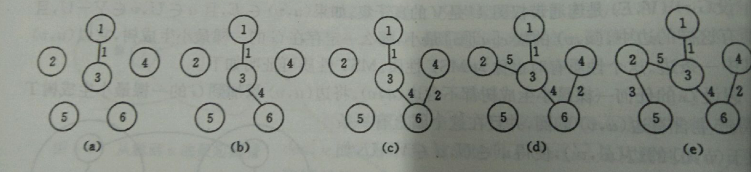
- 我们选择一个起点,然后在与起点相连且未被选的顶点中选择一个权值最小的顶点,将该顶点与其相连边添加入生成树。假设起点是 1 顶点,与 1 顶点相连且未被选的顶点是 {2,3,4},分别对应的权值是 {6,1,5},可见当前最小的权值 1,权值最小的顶点就是 3 顶点,所以将 3 顶点和 1-3 的边添加入生成树。
- 接着我们在与已选顶点相连且未被选的顶点中选择一个权值最小的顶点,将该顶点与其相连边添加入生成树。当前已选顶点是 1、3 顶点,与已选顶点相连且未被选的顶点有 {2,3,4,5},而当前最小的权值 4,权值最小的顶点就是 6 顶点,所以将 6 顶点和 3-6 的边添加入生成树。
- 接着我们依照上一次的步骤继续在与已选顶点相连且未被选的顶点中选择一个权值最小的顶点,将该顶点与其相连边添加入生成树。最终图 e 就是我们通过 Prim 算法得到的最小生成树了。
5. 图的最短路径法
最短路径的概念:从有向图中某一顶点(起始顶点)到达另一顶点(终止顶点)的路径中,其权值之和最小的路径。简单来说就是找出两个顶点间可通行的花费最少的方式,如下图所示。
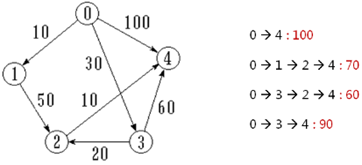
由于交通运输工具和通信工具的便利和普及,两地之间发生货物或者进行信息传递时,最短路径(The Shortest Path)的问题随时都可能因需求而产生。
最小成本生成树(MST)计算的是连通网络中每一个顶点所需的最少花费,但是连通树中任意两顶点的路径不一定是一条花费最少的路径,这也是研究最短路径问题的主要理由。一般讨论的方向有两种:一种是 Dijkstra(迪杰斯特拉)算法,另一种是 Floyd(弗洛伊德)算法。
Dijkstra 算法(迪杰斯特拉算法)
一个顶点到多个顶点的最短路径通常使用 Dijkstra 算法求得,其核心是通过已知最短路径寻找未知最短路径,本质是贪心思想。
Dijkstra 是单源最短路算法,不能处理带负边权的情况,用邻接矩阵或邻接表存图。
解决思路:首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的。所谓松弛就是遍历一遍看看通过刚刚找到的距离最短的点作为中转站到其他顶点会不会更近,如果更近了就更新距离。这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。
- 声明一个数组 dis 来保存起始点到各个顶点的最短距离,和一个保存已经找到了最短路径的顶点的集合 S。
- 初始时,源点 s 的路径权重被赋为 0(dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s, m),则把 dis[m] 设为 w(s, m),同时把所有其他(s 不能直接到达的)顶点的路径长度设为无穷大。因此初始时,集合 S 只有顶点 s。
- 从 dis 数组选择最小值,则该值就是源点 s 到该值对应的顶点的最短路径,并且把该点加入到 S 中,此时完成一个顶点。
- 我们需要看看新加入的顶点是否可以到达其他顶点,并且进行松弛,即看看通过该顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在 dis 中的值。
- 从 dis 中找出最小值,重复上述动作,直到 S 中包含了图的所有顶点。
图解 Dijkstra 算法
以下图为示例,求从顶点 v1 到其他各个顶点的最短路径。
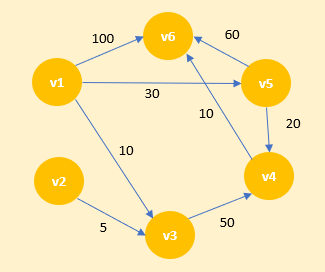
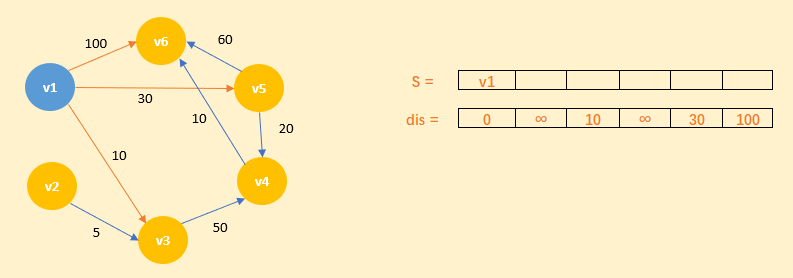
1)首先将v1 顶点进行标识,并作为当前顶点。以此声明一个 dis 数组和集合 S。如下图所示:
集合 S:初始化为 {v1}。
dis 数组:源点 v1 的路径权重被赋为 0,v1 不能到达的 v2 和 v4 顶点则赋为 ∞,其余能达到的顶点则按权重赋值。
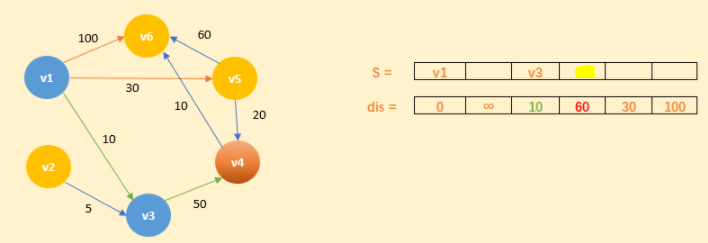
2)求 v1 顶点到其余各个顶点的最短路程。如下图所示:
先找一个离v1 顶点最近的顶点。通过数组 dis 可知当前离 v1 顶点最近是 v3 顶点。当选择了 v3 顶点后,dis[2](下标从0开始)的值(即加入了集合 s 的顶点在 dis 中对应的值)就已经从“估计值”变为了“确定值”,即 v1 顶点到 v3 顶点的最短路程就是当前 dis[2] 值。并将 v3 加入到 S 中。
为什么 v1 顶点到 v3 顶点的最短路径即 0 -> 10 呢?因为目前离 v1 顶点最近的是 v3 顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 v1 顶点到 v3 顶点的路程进一步缩短了。因为 v1 顶点到其它顶点的路程肯定没有 v1 到 v3 顶点短。

3)将顶点 v3 进行标识,并作为当前顶点
下面我们根据这个新入的顶点 v3 的出度,发现以 v3 为弧尾的有:< v3,v4 >,那么我们看看路径:v1–v3–v4 的长度是否比 v1–v4 短。其实这个已经是很明显的了,因为 dis[3] 代表的就是 v1–v4 的长度为无穷大,而 v1–v3–v4 的长度为:10+50=60,所以更新 dis[3] 的值,得到如下结果:
dis[3] 更新为 60 的这个过程有个专业术语叫做“松弛”。即 v1 顶点到 v4 顶点的路程即 dis[3],通过 <v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛 v1 顶点到其余各个顶点的路程。
4)将顶点 v5 进行标识,并作为当前顶点
我们又从除了 dis[2] 和 dis[0] 外的其他值中寻找最小值,发现 dis[4] 的值最小,通过之前解释的原理,可以知道 v1到 v5 的最短距离就是 dis[4] 的值,然后,我们把 v5 加入到集合 S 中,然后,考虑 v5 的出度是否会影响我们的数组 dis 的值,v5有两条出度:< v5,v4> 和 < v5,v6>,然后我们发现 v1–v5–v4 的长度为:50,而 dis[3] 的值为 60,所以我们要更新 dis[3] 的值。另外,v1-v5-v6 的长度为:90,而 dis[5] 为 100,所以我们也需要更新 dis[5] 的值。更新后的 dis 数组如下图: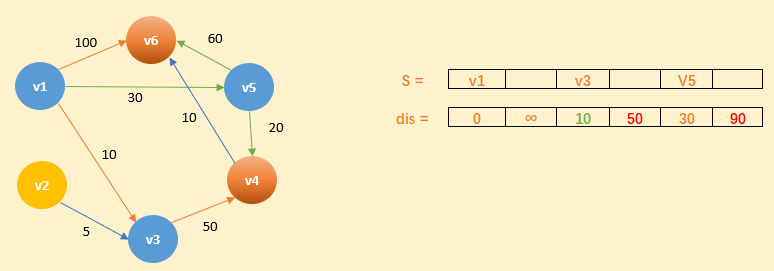
4)将顶点 v4 进行标识,并作为当前顶点
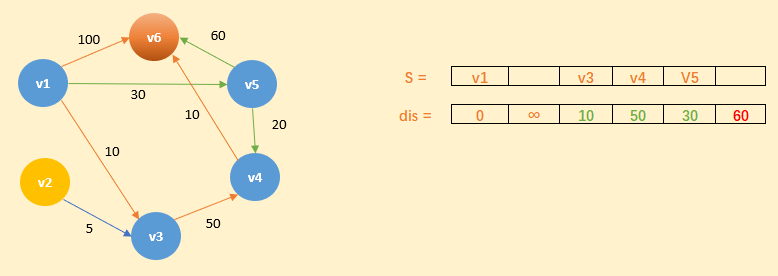
5)同理,分别确定了 v6 和 v2 的最短路径,最后 dis 的数组的值如下:
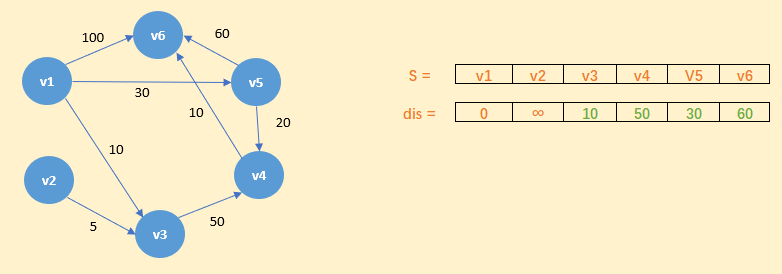
从图中,我们可以发现 v1-v2 的值为 ∞,代表没有路径从 v1 到达 v2。
最后,我们得到 v1 顶点到其他各顶点的最短距离为:
起点 终点 最短路径 长度 v1 v2 无 ∞ v3 {v1,v3} 10 v4 {v1,v5,v4} 50 v5 {v1,v5} 30 v6 {v1,v5,v4,v6} 60
代码实现
1 # 图数组的长度 2 SIZE = 7 3 # 顶点个数 4 VERT_NUMS = 6 5 # 设置无穷大 6 INFINITE = 99999 7 8 9 # 带权图的邻接矩阵算法 10 def adjacency_matrix(arr): 11 # 矩阵中的行和列的索引默认从1开始,所以长度要+1 12 n = SIZE 13 # 初始化结果矩阵(n*n),INFINITE 是为了方便后续 Dijkstra 算法的使用 14 result_arr = [[INFINITE]*n for row in range(n)] 15 16 # 读取图的每条边的数据,获取起始和终止顶点 17 for i in range(len(arr)): 18 tmp_i = arr[i][0] # 起始顶点 19 tmp_j = arr[i][1] # 终止顶点 20 result_arr[tmp_i][tmp_j] = arr[i][2] # 填入权值 21 22 # 输出结果 23 print("邻接矩阵:") 24 for i in range(1, n): 25 for j in range(1, n): 26 print("%s " % result_arr[i][j], end=" ") 27 print() 28 return result_arr 29 30 31 # Dijkstra:单顶点对全部顶点的最短距离 32 def short_cost_path(matrix, start_vertex, vertex_nums): 33 # matrix 邻接矩阵 34 # start_vertex 起始顶点 35 # vertex_nums 总顶点数 36 37 # 记录当前最短距离的顶点 38 shortest_vertex = 1 # 默认从顶点1开始,因此最近的是自己 39 s = [0] * SIZE # 集合S:记录该顶点是否被选取 40 # 路径成本数组 41 dis = [INFINITE] * SIZE 42 # 初始化起始顶点的dis 43 for i in range(1, SIZE): 44 dis[i] = matrix[start_vertex][i] 45 s[start_vertex] = 1 # 将起始顶点加入集合s 46 dis[start_vertex] = 0 47 48 # 遍历剩下的全部顶点 49 for i in range(1, vertex_nums): 50 shortest_distance = INFINITE 51 for j in range(1, vertex_nums+1): 52 # 遍历dis,找出最小距离的下一顶点 53 if s[j] == 0 and shortest_distance > dis[j]: 54 shortest_distance = dis[j] 55 shortest_vertex = j 56 # 将最小距离的下一顶点加入集合s 57 s[shortest_vertex] = 1 58 # 松弛:开始计算当前顶点到各出度顶点的最短距离 59 for j in range(vertex_nums+1): 60 # s[j] == 0 表示未在集合s中的出度顶点 61 # dis[shortest_vertex]:起始点到当前顶点的暂时最短距离 62 # matrix[shortest_vertex][j]:当前顶点到出度顶点的距离 63 # dis[j]:起始点到出度顶点的距离 64 if s[j] == 0 and dis[shortest_vertex] + matrix[shortest_vertex][j] < dis[j]: 65 dis[j] = dis[shortest_vertex] + matrix[shortest_vertex][j] 66 67 return dis 68 69 70 path_cost = [[1,3,10], [1,5,30], [1,6,100], [2,3,5], [3,4,50], [4,6,10], [5,4,20], [5,6,60]] 71 matrix = adjacency_matrix(path_cost) 72 print() 73 # 搜索顶点1到其他顶点的最短路径 74 dis = short_cost_path(matrix, 1, VERT_NUMS) 75 print("*"*50) 76 print("顶点1到各顶点的最短距离为:") 77 print("*"*50) 78 for i in range(1, SIZE): 79 print("顶点 1 到顶点 %d 的最短距离=%d"%(i, dis[i]))
执行结果:
1 邻接矩阵: 2 99999 99999 10 99999 30 100 3 99999 99999 5 99999 99999 99999 4 99999 99999 99999 50 99999 99999 5 99999 99999 99999 99999 99999 10 6 99999 99999 99999 20 99999 60 7 99999 99999 99999 99999 99999 99999 8 9 ************************************************** 10 顶点1到各顶点的最短距离为: 11 ************************************************** 12 顶点 1 到顶点 1 的最短距离=0 13 顶点 1 到顶点 2 的最短距离=99999 14 顶点 1 到顶点 3 的最短距离=10 15 顶点 1 到顶点 4 的最短距离=50 16 顶点 1 到顶点 5 的最短距离=30 17 顶点 1 到顶点 6 的最短距离=60
Floyd 算法(弗洛伊德算法)
Dijkstra 算法只能求出某一点其他顶点的最短距离,如果要求出图中任意两点甚至所有顶点间的最短距离(也被称为“多源最短路径问题”),那么就需要使用 Floyd 算法。
求图中所有顶点间的最短路径,有以下两种解法:
- 以图中的每个顶点作为起始点,调用 Dijkstra 算法,时间复杂度为 O(n3)。
- Floyd 算法更简洁,时间复杂度仍为 O(n3),空间复杂度为 O(n2)。
Floyd 算法是一个经典的动态规划算法,三个 for 循环便可以解决一个复杂的问题,其算法实现相比 Dijkstra 等算法是非常优雅的,可读性高,理解起来较为容易。从它的三层循环可以看出其时间复杂度为 O(n3),除了在第二层 for 中加点判断可以略微提高效率,几乎没有其他办法再减少它的复杂度。
比较两种算法,不难得出以下的结论:
- 对于稀疏图,采用 n 次 Dijkstra 比较出色;对于稠密图,使用 Floyd 算法效果更佳。
- Floyd 算法可以处理带负边的图。
图解 Floyd 算法
- Floyd 算法首先初始化一个矩阵 S,记录着顶点间的最小路径。例如 S[0][3] = 10,说明顶点 0 到 3 的最短路径为 10。
- 然后通过 3 重循环,k 为中转点,v 为起点,w 为终点,循环比较 S[v][w] 和 S[v][k] + S[k][w] 最小值,如果 S[v][k] + S[k][w] 为更小值,则把 S[v][k] + S[k][w] 覆盖保存在 S[v][w] 中。
如下图所示:
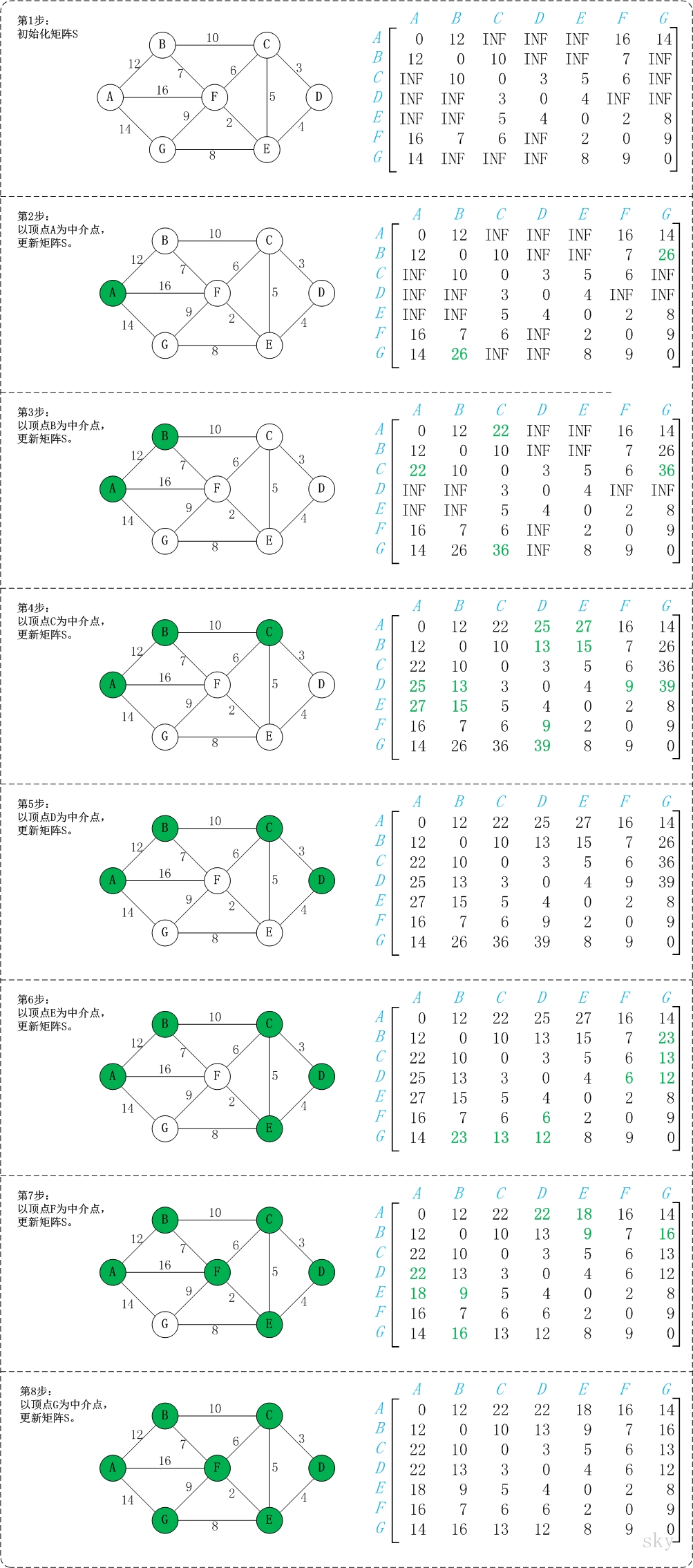
- 矩阵 S 中,顶点 S[i][j] 的距离为顶点 i 到顶点 j 的权值;如果 i 和 j 不相邻,则 a[i][j] = ∞。
- 以 A 为中转点,找出 S[i][j] 从 i 到 j,经由顶点 A 的最短路径,并更新矩阵。如原 S 矩阵中,S[B][G] 的值为 INF,即不存在 B->G 的最小路径,但是通过 A 为中转点,S[B][A] + S[A][G] = 12 + 14 = 26 小于 S[B][G] = INF, 所以 S[B][A] + D[A][G] 为 B -> G 的最小值,因此覆盖 S[B][G] 为 26。
- 以 B 为中转点,找出 S[i][j] 从 i 到 j,经由顶点 B 的最短路径,并更新矩阵。如 S[A][C] 的值为 INF, 但是通过 B 作为中转点,S[A][B] + S[B][C] = 12 + 10 = 22 小于 S[A][C] = INF,所以 S[A][B] + S[B][C] 为 A->C 的最小路径,覆盖 S[A][C] 的值为 22。
- 以此类推,当遍历完所有顶点,矩阵 S 中记录的便是各顶点间的最短路径。
代码实现
1 # 顶点个数 2 VERT_NUMS = 7 3 # 图数组的长度 4 SIZE = 8 5 # 设置无穷大 6 INFINITE = 99999 7 8 9 # 带权图的邻接矩阵算法 10 def adjacency_matrix(arr): 11 # 矩阵中的行和列的索引默认从1开始,所以长度要+1 12 n = SIZE 13 # 初始化结果矩阵(n*n),INFINITE 是为了方便后续算法的使用 14 result_arr = [[INFINITE]*n for row in range(n)] 15 16 for i in range(n): 17 for j in range(n): 18 if i == j: 19 result_arr[i][j] = 0 # 对角线设为0 20 21 # 读取图的每条边的数据,获取起始和终止顶点 22 for i in range(len(arr)): 23 tmp_i = arr[i][0] # 起始顶点 24 tmp_j = arr[i][1] # 终止顶点 25 result_arr[tmp_i][tmp_j] = arr[i][2] # 填入权值 26 27 # 输出结果 28 print("邻接矩阵:") 29 for i in range(1, n): 30 for j in range(1, n): 31 print("%s " % result_arr[i][j], end="\t") 32 print() 33 return result_arr 34 35 36 # 任意两点间的最短距离 37 def short_cost_path(matrix, vertex_nums): 38 # matrix 邻接矩阵 39 # vertex_nums 总顶点数 40 41 # 初始化结果矩阵:即复制传入的初始化的邻接矩阵 42 dis = matrix[:] 43 44 # 使用Floyd 算法找出所有顶点间的最短距离 45 for k in range(1, vertex_nums+1): 46 for i in range(1, vertex_nums+1): 47 for j in range(1, vertex_nums+1): 48 if dis[i][k] + dis[k][j] < dis[i][j]: 49 dis[i][j] = dis[i][k] + dis[k][j] 50 return dis 51 52 53 path_cost = [[1,2,12], [2,1,12], [1,6,16], [6,1,16], [1,7,14], [7,1,14], [2,3,10], [2,6,7], \ 54 [3,2,10], [3,6,6], [3,4,3], [3,5,5], [4,3,3], [4,5,4], [5,3,5], [5,4,4], [5,6,2], [5,7,8], \ 55 [6,2,7], [6,3,6],[6,5,2], [6,7,9], [7,6,9], [7,5,8]] 56 57 matrix = adjacency_matrix(path_cost) 58 print() 59 # 搜索各顶点间的最短路径 60 dis = short_cost_path(matrix, VERT_NUMS) 61 print("*"*70) 62 print("顶点间的最短距离:") 63 print("*"*70) 64 print(" 顶点1 顶点2 顶点3 顶点4 顶点5 顶点6 顶点7") 65 for i in range(1, SIZE): 66 print("顶点%d"%i, end="\t") 67 for j in range(1, SIZE): 68 print("%d"%dis[i][j], end="\t") 69 print()
执行结果:
邻接矩阵: 0 12 99999 99999 99999 16 14 12 0 10 99999 99999 7 99999 99999 10 0 3 5 6 99999 99999 99999 3 0 4 99999 99999 99999 99999 5 4 0 2 8 16 7 6 99999 2 0 9 14 99999 99999 99999 8 9 0 ********************************************************************** 顶点间的最短距离: ********************************************************************** 顶点1 顶点2 顶点3 顶点4 顶点5 顶点6 顶点7 顶点1 0 12 22 22 18 16 14 顶点2 12 0 10 13 9 7 16 顶点3 22 10 0 3 5 6 13 顶点4 22 13 3 0 4 6 12 顶点5 18 9 5 4 0 2 8 顶点6 16 7 6 6 2 0 9 顶点7 14 16 13 12 8 9 0


 浙公网安备 33010602011771号
浙公网安备 33010602011771号