矩阵及其算法

1. 矩阵介绍

2. 矩阵相加

3. 矩阵相乘

4. 矩阵转置

 

  

1. 矩阵介绍

矩阵（matrix）是数字或字符的矩形网格（如 excel 表格），并具有加、减、乘等运算规则。

从数学的角度来看，对于 m x n 矩阵的形式，可以用计算机中的二维数组来表示。基本上，许多矩阵的运算与应用都可以使用计算机中的二维数组解决。

矩阵维度

我们用 (行数, 列数) 来描述矩阵的维度。

 

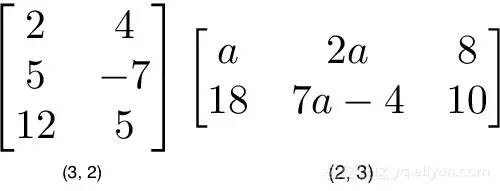
2. 矩阵相加

矩阵的相加运算较为简单，前提是相加的两个矩阵对应的行数与列数必须相等，而相加后矩阵的行数与列数也是相同的。

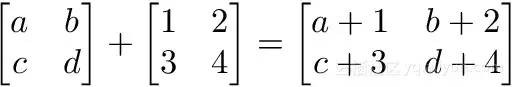
示例代码

A = [[1,2,3], [1,2,3], [1,2,3]]
B = [[1,2,3], [1,2,3], [1,2,3]]
N = 3
# 用于存放相加结果的矩阵
C = [[None]*N for i in range(N)]

for i in range(N):
    for j in range(N):
        C[i][j] = A[i][j] + B[i][j]  # 矩阵C = 矩阵A + 矩阵B
print("矩阵A和矩阵B的相加结果：")
for i in range(N):
    for j in range(N):
        print(C[i][j], end="\t")
    print()

执行结果：

矩阵A和矩阵B的相加结果：
2       4       6
2       4       6
2       4       6

 

3. 矩阵相乘

并不是所有的矩阵都能进行乘法运算的。 并且，对输出矩阵的维度也存在要求。

矩阵一的列数必须等于矩阵二的行数，如 M×N 矩阵和 N×K 矩阵相乘的结果是 M×K 矩阵（新矩阵取矩阵一的行和矩阵二的列）。

实现原理

矩阵乘法依赖于点积与行列元素的各种组合。 以下图为例，矩阵 C 中的每个元素都是矩阵 A 的行与矩阵 B 的列的点积。

操作 a1·b1 表示我们取矩阵 A 中第 1 行 (1,7) 和矩阵 B 中第 1 列 (3,5) 的点积：

即：

为什么矩阵乘法以这种方式工作？

矩阵的乘法运算非常有用，但背后并没有太深奥的数学规律，之所以数学家发明了这种运算，完全是因为它简化了以前乏味的计算。这是一个人为的产物，但却非常有效。

示例代码

# 矩阵相乘函数
def matrix_multiply(matrix1, matrix2):
        # 初始化所需的维度
    m = len(matrix1)  # matrix1的行数
    n = len(matrix1[0])  # matrix1的列数 即matrix2的行数
    p = len(matrix2[0])  # matrix2的列数

    # 初始化结果矩阵 = matrix1的行数 x matrix2的列数
    result_matrix = [[None]*p for i in range(m)]

    for row_no in range(m):
        for col_no in range(p):
            tmp = 0
            for k in range(n):
                tmp = tmp + matrix1[row_no][k] * matrix2[k][col_no]
            result_matrix[row_no][col_no] = tmp
    return result_matrix


A = [[1,2,3], [4,5,6], [7,8,9]]
B = [[1,2], [3,4], [5,6]]

result_matrix = matrix_multiply(A, B)

print("矩阵相乘结果：")
for i in range(len(result_matrix)):
    for j in range(len(result_matrix[0])):
        print(result_matrix[i][j], end="\t")
    print()

执行结果：

矩阵相乘结果：
22      28
49      64
76      100

 

4. 矩阵转置

转置矩阵（A^T）就是把原矩阵的行坐标元素与列坐标元素相互调换。假设 A^T 为 A 的转置矩阵，则有 A^T[j, i] = A[i, j]。

转置矩阵有两个步骤：

1. 矩阵旋转 90°
2. 反转每行元素的顺序（例如 [a b c] 变为 [c b a]）

例如，将矩阵 M 转置为 T：

示例代码

# 转置矩阵函数
def matrix_t(matrix):
    result_matrix = [[None]*len(matrix) for i in range(len(matrix[0]))]
    for i in range(len(matrix)):
        for j in range(len(matrix[0])):
            result_matrix[j][i] = matrix[i][j]
    return result_matrix


A = [[1,2], [3,4], [5,6]]

result_matrix = matrix_t(A)
print("矩阵转置结果：")
for i in result_matrix:
    for j in i:
        print(j, end="\t")
    print()