排序算法

排序算法简介

1. 冒泡排序

2. 选择排序

3. 插入排序

4. 希尔排序

5. 快速排序

6. 归并排序

 

 

排序算法简介

排序算法（英语：Sorting algorithm）是一种能将一串数据依照特定顺序进行排列的一种算法。

排序算法的稳定性

稳定性：稳定排序算法会让原本有相等键值的纪录维持其相对次序。也就是如果一个排序算法是稳定的，当有两个相等键值的纪录 R 和 S，且在原本的列表中 R 出现在 S 之前，在排序过的列表中 R 也将会是在 S 之前。

当相等的元素是无法分辨的，比如像是整数，稳定性并不是一个问题。然而，假设以下的数对将要以他们的第一个数字来排序。

(4, 1) (3, 1) (3, 7) (5, 6)

在这个状况下，有可能产生两种不同的结果，一个是让相等键值的纪录维持相对的次序，而另外一个则没有：

(3, 1) (3, 7) (4, 1) (5, 6)  （维持次序）
(3, 7) (3, 1) (4, 1) (5, 6)  （次序被改变）

不稳定排序算法可能会在相等的键值中改变纪录的相对次序，但是稳定排序算法从来不会如此。

不稳定排序算法可以被特别地实现为稳定，做这件事情的一个方式是人工扩充键值的比较，如此在其他方面相同键值的两个对象间之比较（比如上面的比较中加入第二个标准：第二个键值的大小），就会被决定使用在原先数据次序中的条目，当作一个同分决赛。然而，要记住这种次序通常牵涉到额外的空间负担。

常见算法效率比较

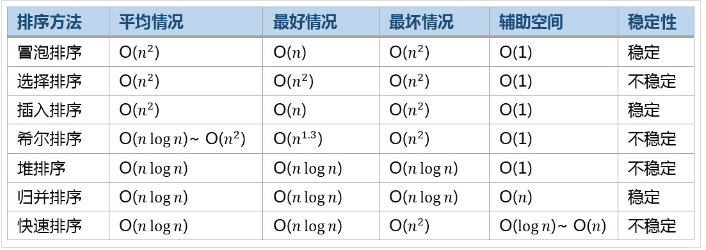
性能从优到劣：

 

1. 冒泡排序

介绍

冒泡排序（英语：Bubble Sort）是一种简单的排序算法，它通过不断地交换“大数”的位置达到排序的目的。因为不断出现“大数”类似于水泡不断出现，因此被形象地称为冒泡排序算法。

它重复地遍历要排序的数列，一次比较两个元素，如果他们的大小顺序有误则把它们交换过来。遍历数列的工作是重复地进行直到没有元素再需要交换，也就是说该数列已经排序完成。

冒泡排序算法的运作如下：

• 比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对元素需要比较。

时间复杂度

• 最优时间复杂度：O(n)（表示第一次遍历发现没有任何可以交换的元素，则排序结束）
• 最坏时间复杂度：O(n²)
• 稳定性：稳定

交换过程图示（第一次遍历）

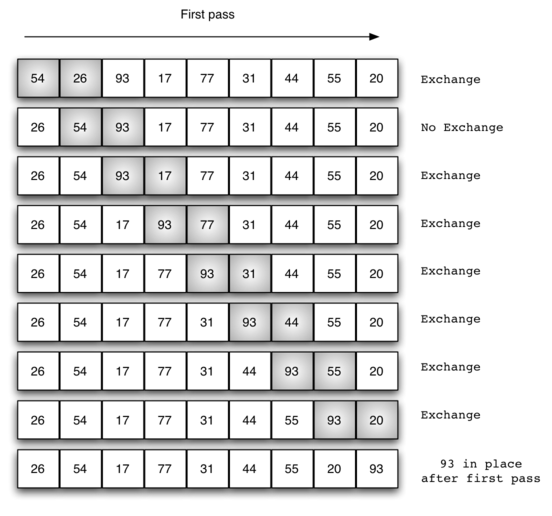
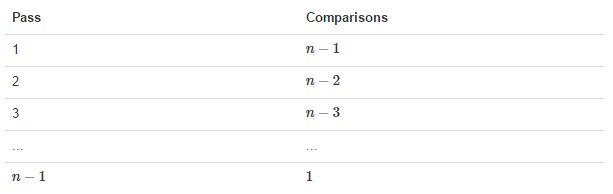
 那么我们需要进行n-1次冒泡过程，每次对应的比较次数如下图所示：

代码实现

Python 版：

def bubble_sort(alist):
    "冒泡排序"
    n = len(alist)
    for j in range(n-1):  # 控制轮数（图示中的Pass）
        count = 0  # 记录每轮中的比较次数
        for i in range(n-1-j):  # 每轮遍历中的元素比较次数，逐渐减少（图示中的Comparisons）；也可以使用 for i in range(n-1, 0, -1); for j in range(i):
            if alist[i] > alist[i+1]:
                alist[i], alist[i+1] = alist[i+1], alist[i]
                count += 1
        # 优化时间复杂度，若该轮没有交换元素，即代表列表已是有序，则无需再进行下一轮比较
        # 即可直接退出
        if count == 0:
            return

                
# j: 0     i: range(n-1-0) = n-1
# j: 1     i: range(n-1-1) = n-2
# j: 2     i: range(n-1-2) = n-3
# ...
# j: n-2   i: range(n-1-(n-2)) = 1


if __name__ == "__main__":
    li = [1, 21, 4, 2, 56, 2, 34, 67]
    bubble_sort(li)
    print(li)  # [1, 2, 2, 4, 21, 34, 56, 67]

Java 版：

    public static void main(String[] args) {
        int[] input = {12, 34, 65, 23, 54, 12, 34, 54};
        bubbleSort(input);
        System.out.println(Arrays.toString(input));
    }

    public static void bubbleSort(int[] arr) {
        int length = arr.length;
        for (int i=0; i<length-1; i++) {
            int changeCount = 0;
            for (int j=0; j<(length-1-i); j++) {
                if (arr[j]>arr[j+1]) {
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                    changeCount ++;
                }
            }
            if (changeCount==0) {
                return;
            }
        }
    }

 

2. 选择排序

选择排序（Selection sort）的算法算是枚举法的应用，就是反复从未排序的数列中取出最小（大）的元素，加入到另一个数列中，最后的结果即为已排序的数列。它的具体工作原理如下：

1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
2. 从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
3. 以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对 n 个元素的数列进行排序总共进行至多 n-1 次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

时间复杂度

• 最优时间复杂度：O(n²)
• 最坏时间复杂度：O(n²)
• 稳定性：不稳定（考虑升序每次选择最大的情况）

Python版的选择排序：

理论上选择排序的时间复杂度为 O(n²)，但在 Python 中较为特殊，因为在 Python 列表中寻找最小的那个数不需要逐个比较，使用 min() 就可以一步到位地得到最小的数，所以使用 Python 版的选择排序，时间复杂度是 O(n)。因此理论上 Python 版本的排序算法中选择排序算法是最快的。

排序过程图示

 

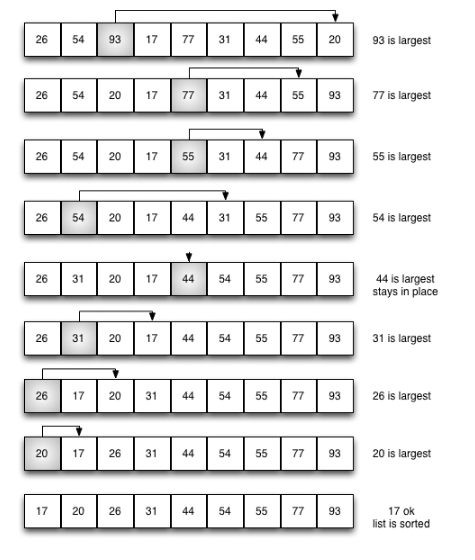
 代码实现：

Python 常规版

def selected_sort(alist):
    n = len(alist)
    # 需要进行n-1次选择操作
    for i in range(n-1):
        # 记录最小位置
        min_index = i
        # 从i+1位置到末尾，选择出最小的元素
        for j in range(i+1, n):
            if alist[j] < alist[min_index]:
                min_index = j
        # 如果选择出的元素不在正确位置，进行交换
        if min_index != i:
            alist[i], alist[min_index] = alist[min_index], alist[i]


alist = [54, 226, 93, 17, 77, 31, 44, 55, 20]
selected_sort(alist)
print(alist)

python 内置的 min()：

import random
import timeit

def random_list(n):
    return [random.randint(0, 100) for i in range(n)]

def selection_sort(i_list):
    if len(i_list) <= 1:
        return i_list
    # 一个长度为n的数列需要排序n-1轮
    for i in range(0, len(i_list)-1):
        if i_list[i] != min(i_list[i:]):
            # 使用min()找到列表剩余元素中的最小值
            min_index = i_list.index(min(i_list[i:]), i)
            i_list[i], i_list[min_index] = i_list[min_index], i_list[i]
        # print("第%s轮的排序结果：%s" % (i+1, i_list))
    return i_list

if __name__ == "__main__":
    i_list = random_list(20)
    print(i_list)
    print(selection_sort(i_list))
    print(timeit.timeit("selection_sort(i_list)", "from __main__ import selection_sort, i_list", number=100))

Java 版：

    public static void main(String[] args) {
        int[] input = {12, 34, 65, 23, 54, 12, 34, 54};
        selectSort(input);
        System.out.println(Arrays.toString(input));
    }

    public static void selectSort(int[] arr) {
        int length = arr.length;
        for (int i=0; i<length-1; i++) {
            int tmpMin = arr[i];
            for (int j=i+1; j<length; j++) {
                if (arr[j]<tmpMin) {
                    tmpMin = arr[j];
                    arr[j] = arr[i];
                    arr[i] = tmpMin;
                }
            }
        }
    }

 

3. 插入排序

插入排序（Insertion Sort）可能是最好理解的排序了。插入排序方法与打扑克取牌的排序很相似，在打扑克时，每取一张新牌，都会与手上已有的牌进行比较，将新牌插入到比自己小的牌后面。等取完所有的牌后，手上已有的牌就是各有序的序列。

它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

当原始序列的元素大部分已排好序的情况下，插入排序会非常有效率，因为它不需要执行太多的数据搬移操作。

时间复杂度

• 最优时间复杂度：O(n)（升序排序时，序列已经处于升序状态）
• 最坏时间复杂度：O(n²)
• 稳定性：稳定

排序过程图示

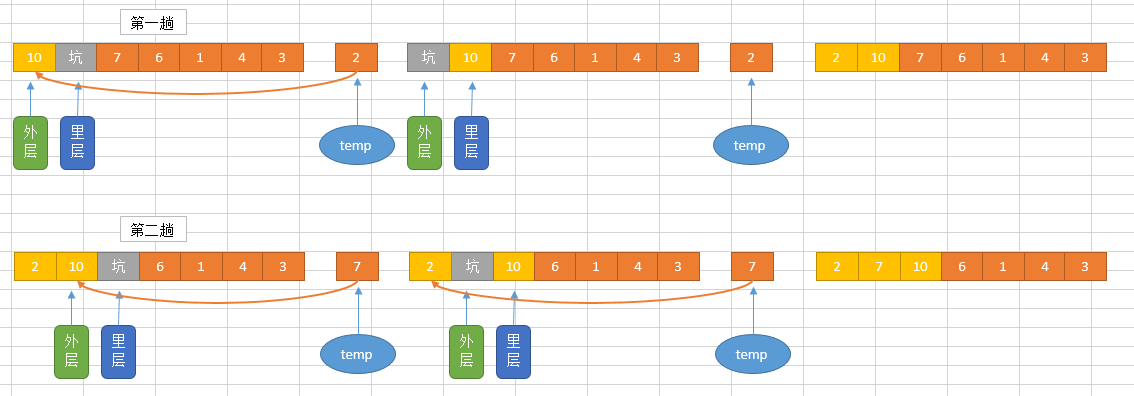
演示效果

代码实现

Python 版：

def insertion_sort(data):
    for i in range(1, len(data)):
        tmp = data[i]  # 暂存数据
        count = i
        while i >= 1 and tmp < data[i-1]:  # 遍历与前一个元素比较
            data[i] = data[i-1]  # 把所有元素往后移一位
            i -= 1
        data[i] = tmp  # 若当前元素大于等于前一个元素，则当前位置放入暂存数据
        print("第%d次排序结果：%s" % (count, data))
    return data


data = [12, 11, 23, 4, 1, 5, 12, 31, 4]
insertion_sort(data)

执行结果：

第1次排序结果：[11, 12, 23, 4, 1, 5, 12, 31, 4]
第2次排序结果：[11, 12, 23, 4, 1, 5, 12, 31, 4]
第3次排序结果：[4, 11, 12, 23, 1, 5, 12, 31, 4]
第4次排序结果：[1, 4, 11, 12, 23, 5, 12, 31, 4]
第5次排序结果：[1, 4, 5, 11, 12, 23, 12, 31, 4]
第6次排序结果：[1, 4, 5, 11, 12, 12, 23, 31, 4]
第7次排序结果：[1, 4, 5, 11, 12, 12, 23, 31, 4]
第8次排序结果：[1, 4, 4, 5, 11, 12, 12, 23, 31]

Java 版：

    public static void main(String[] args) {
        int[] input = {12, 34, 65, 23, 54, 12, 34, 54, 17};
        insertSort(input);
        System.out.println(Arrays.toString(input));
    }

    public static void insertSort(int[] arr) {
        for (int i=1; i<arr.length; i++) {
            int tmp = arr[i];
            for (int j=i; j>0; j--) {
                if (tmp<arr[j-1]) {
                    arr[j]=arr[j-1];
                } else {
                    arr[j] = tmp;
                    break;
                }
            }
        }
    }

 

4. 希尔排序

希尔排序（Shell Sort）是插入排序算法的一种更高效的改进版本。该方法因 DL.Shell 于 1959 年提出而得名。

希尔排序的基本思想是：将数组列在一个表中，并对每一列进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行，最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身还是使用数组进行排序。

时间复杂度

• 最优时间复杂度：根据步长序列的不同而不同
• 最坏时间复杂度：O(n²)
• 稳定性：不稳定

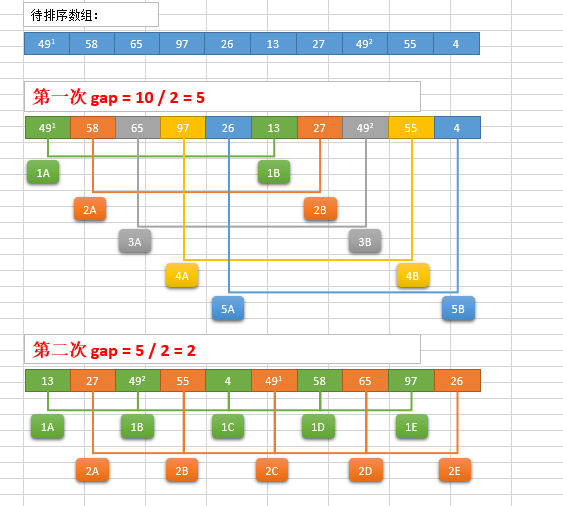
希尔排序过程

例如，假设有这样一组数 [13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10]，如果我们以步长为 5 开始进行排序，我们可以通过将这列表放在有 5 列的表中来更好地描述算法，这样他们就应该看起来是这样（竖着的元素是步长组成）：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45]。这时 10 已经移至正确位置了，然后再以 3 为步长进行排序：

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之后变为：

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最后以 1 步长进行排序（此时就是简单的插入排序了）。

示例分析

代码实现

# 希尔排序
def shell_sort(alist):
    count = 1  # 打印排序次数
    n = len(alist)
    gap = n // 2  # 步长需通过数学计算，质数最好。为了算法方便，习惯选2
    # gap变化到0前，子序列插入算法执行的次数
    while gap > 0:
        # 子序列的插入算法，与普通插入算法区别在于gap步长
        for i in range(gap, n):
            tmp = alist[i]
            while i >= gap and tmp < alist[i-gap]:  # 每组子序列中，当前元素与前gap个元素比较
                alist[i] = alist[i-gap]
                i -= gap
            alist[i] = tmp
        print("gap=%d, 第%d次排序的结果：%s" % (gap, count, alist))
        # 每轮排序对半缩短gap
        gap //= 2
        count += 1


alist = [63, 92, 27, 36, 45, 71, 58, 7]
shell_sort(alist)

执行结果：

gap=4, 第1次排序的结果：[45, 71, 27, 7, 63, 92, 58, 36]
gap=2, 第2次排序的结果：[27, 7, 45, 36, 58, 71, 63, 92]
gap=1, 第3次排序的结果：[7, 27, 36, 45, 58, 63, 71, 92]

 

5. 快速排序

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），是目前公认最佳的排序法。它通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

步骤为：

1. 从数列中挑出一个元素，称为“基准”(pivot)。
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

时间复杂度

• 最优时间复杂度：O(nlogn)
• 最坏时间复杂度：O(n²)
• 稳定性：不稳定

排序过程图示

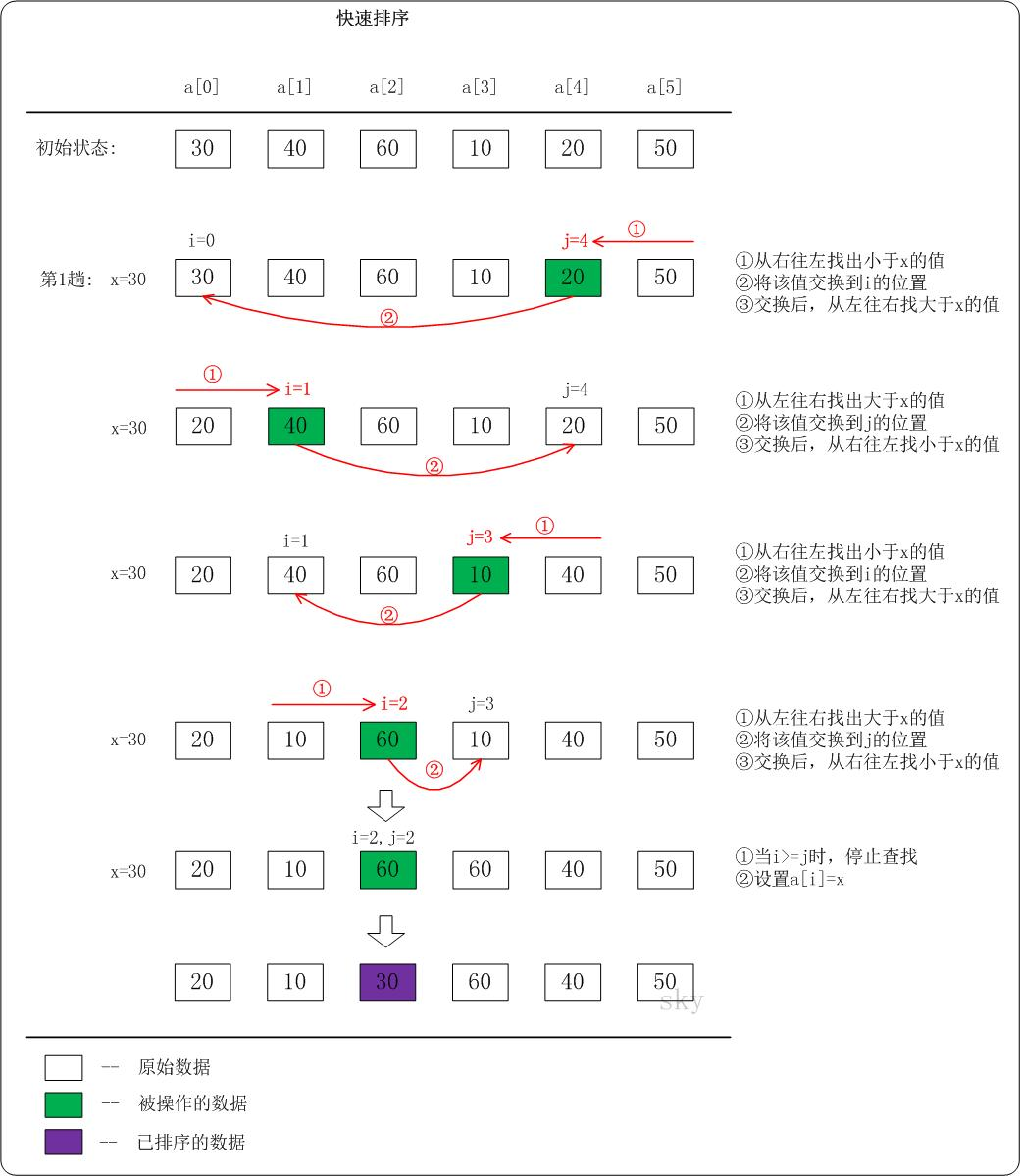
 代码实现

Python 版：

def quick_sort(alist, start, end):
    # 递归的退出条件
    if start >= end:
        return
    # 设定起始元素为要寻找位置的基准元素
    mid_value = alist[start]
    # low为从左往右的游标
    low = start
    # high为从右往左的游标
    high = end
    # 当low与high未重合
    while low < high:
        # 当low与high未重合时，若high指向的元素不比基准元素小，则high向左移动一位
        while low < high and alist[high] >= mid_value:
            high -= 1
        # 若high指向的元素比基准元素小，则退出循环，交换元素位置
        alist[low] = alist[high]
        # 当low与high未重合时，若low指向的元素比基准元素小，则low向右移动一位
        while low < high and alist[low] < mid_value:
            low += 1
        # 若low指向的元素比基准元素大，则推出循环，交换元素位置
        alist[high] = alist[low]
    # 当low与high重合，退出循环，此时所指位置为基准元素的正确位置
    # 将基准元素放到该位置
    alist[low] = mid_value
    # 对基准元素左边的子序列进行递归快速排序
    quick_sort(alist, start, low-1)
    # 对基准元素右边的子序列进行递归快速排序
    quick_sort(alist, low+1, end)


alist = [54, 226, 93, 17, 77, 31, 44, 55, 20]
quick_sort(alist, 0, len(alist)-1)
print(alist)

Java 版：

import java.util.Arrays;

public class Demo {

    public static void main(String[] args) {
        int[] arr = new int[]{21,13,4,16,7,39,4,10};
        quickSort(arr, 0, arr.length-1);
        System.out.println(Arrays.toString(arr));  // [4, 4, 7, 10, 13, 16, 21, 39]
    }

    // 快排
    public static void quickSort(int[] arr, int start, int end) {
        if (start>=end) {
            return;
        }
        int standard = arr[start];
        int left = start;
        int right = end;
        while (left<right) {
            while (left < right && arr[right] >= standard) {
                right--;
            }
            arr[left] = arr[right];
            while (left < right && arr[left] < standard) {
                left++;
            }
            arr[right] = arr[left];
        }
        arr[left] = standard;
        quickSort(arr, start, left-1);
        quickSort(arr, left+1, end);
    }
}

时间复杂度 O(nlogn) 分析：

• 在最好的情况下，每次运算一次分区，我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此，在到达大小为一的数列前，我们只要作 logn 次嵌套的调用，这个意思就是调用树的深度是 O(logn)。
• 同时，在同一层次结构的左右两个递归调用中，不会处理到原来数列的相同部分。因此，程序调用的每一层次结构总共全部仅需要 O(n) 的时间（每次调用会有某些共同的额外耗费，但是因为在每一层次结构仅仅只有 O(n) 个调用，这些被归纳在 O(n) 系数中）。

 

6. 归并排序

归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

将数组分解最小之后，然后合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

时间复杂度

• 最优时间复杂度：O(nlogn)
• 最坏时间复杂度：O(nlogn)
• 稳定性：稳定

归并排序的分析

 

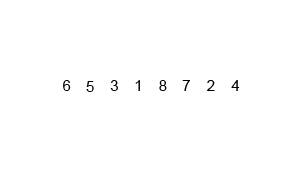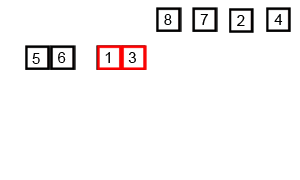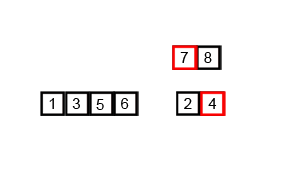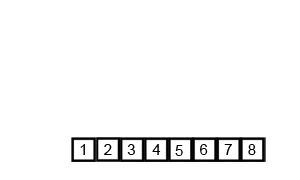
 代码实现：版本一

def merge_sort(alist):
    """归并排序"""
    n = len(alist)
    if n <= 1:
        return alist
    mid = n // 2
    # left 采用归并排序后形成的有序的新的列表
    left_li = merge_sort(alist[:mid])
    # right 采用归并排序后形成的有序的新的列表
    right_li = merge_sort(alist[mid:])

    # 将两个有序的子序列合并为一个新的整体
    # merge(left, right)
    left_pointer, right_pointer = 0, 0
    result = []

    while left_pointer < len(left_li) and right_pointer < len(right_li):
        if left_li[left_pointer] <=  right_li[right_pointer]:
            result.append(left_li[left_pointer])
            left_pointer += 1
        else:
            result.append(right_li[right_pointer])
            right_pointer += 1

    result += left_li[left_pointer:]
    result += right_li[right_pointer:]
    return result


if __name__ == "__main__":
    li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print(li)
    sorted_li = merge_sort(li)
    print(li)
    print(sorted_li)

版本二

import random
import timeit

def random_list(n):
    return [random.randint(0, 100) for i in range(n)]

def merge_sort(i_list):
    if len(i_list) <= 1:
        return i_list
    mid = len(i_list) // 2
    left, right = i_list[:mid], i_list[mid:]
    # 将左右子数列再拆分成左右子子子……数列
    return merge_list(merge_sort(left), merge_sort(right))

# 将左右两个有序数列进行合并
def merge_list(left, right):
    result_list = []
    while left and right:
        if left[0] >= right[0]:
            result_list.append(right.pop(0))
        else:
            result_list.append(left.pop(0))
    result_list.extend(left)
    result_list.extend(right)
    return result_list

if __name__ == "__main__":
    i_list = random_list(20)
    print(i_list)
    print(merge_sort(i_list))
    print(timeit.timeit("merge_sort(i_list)", "from __main__ import merge_sort, i_list", number=100))