数据结构与算法 介绍

1. 引入：算法的提出

2. 算法的效率衡量：时间复杂度

3. 常见的时间复杂度

4. Python 内置类型性能分析

5. 数据结构

 

 

1. 引入：算法的提出

先来看一道题：

如果 a+b+c=1000，且 a²+b²=c²（a、b、c 为自然数），如何求出所有 a、b、c 可能的组合?

第一次尝试

import time 

start_time = time.time()

# 三重循环
for a in range(1001):
    for b in range(1001):
        for c in range(1001):
            if a + b + c == 1000 and a**2 + b**2 == c**2:
                print("a:{}, b:{}, c:{}".format(a, b, c))
                
end_time = time.time()
print("used time: %f" % (end_time-start_time))
print("complete!")

运行结果：

a:0, b:500, c:500
a:200, b:375, c:425
a:375, b:200, c:425
a:500, b:0, c:500
used time: 620 seconds
complete!

算法的提出

算法的概念

算法是计算机处理信息的本质，因为计算机程序本质上是一个算法来告诉计算机按照确切的步骤来执行一个指定的任务。一般地，当算法在处理信息时，会从输入设备或数据的存储地址读取数据，把结果写入输出设备或某个存储地址供以后再调用。

算法是独立存在的一种解决问题的方法和思想。对于算法而言，实现的语言并不重要，重要的是思想。

算法可以有不同的语言描述实现版本（如 C 描述、C++ 描述、Python 描述等），我们现在是在用 Python 语言进行描述实现。

算法的五大特性

1. 输入：算法具有 0 个或多个输入。
2. 输出：算法至少有 1 个或多个输出。
3. 有穷性：算法在有限的步骤之后会自动结束而不会无限循环，并且每一个步骤可以在可接受的时间内完成。
4. 确定性：算法中的每一步都有确定的含义，不会出现二义性。
5. 可行性：算法的每一步都是可行的，也就是说每一步都能够执行有限的次数完成。

第二次尝试

import time 

start_time = time.time()

# 两重循环
for a in range(1001):
    for b in range(1001):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a:{}, b:{}, c:{}".format(a, b, c))
                
end_time = time.time()
print("used time: %f seconds" % (end_time-start_time))
print("complete!")

运行结果：

a:0, b:500, c:500
a:200, b:375, c:425
a:375, b:200, c:425
a:500, b:0, c:500
used time: 4 seconds
complete!

 

2. 算法的效率衡量：时间复杂度

执行时间

执行时间反应算法效率

对于同一问题，我们给出了两种解决算法，在两种算法的实现中，我们对程序执行的时间进行了测算，发现两段程序执行的时间相差悬殊（620秒相比于4秒），由此我们可以得出结论：实现算法程序的执行时间可以反应出算法的效率，即算法的优劣。

单靠时间值绝对可信吗？

假设我们将第二次尝试的算法程序运行在一台配置古老性能低下的计算机中，情况会如何？很可能运行的时间并不会比在我们的电脑中运行算法一的执行时间快多少。因此，单纯依靠运行的时间来比较算法的优劣并不一定是客观准确的！

程序的运行离不开计算机环境（包括硬件和操作系统），这些客观原因会影响程序运行的速度并反应在程序的执行时间上。那么如何才能客观的评判一个算法的优劣呢？

* 时间复杂度

我们假定计算机执行算法时每一个基本操作（即计算步骤）的时间是固定的一个时间单位，那么有多少个基本操作就代表会花费多少时间单位。当然，对于不同的机器环境而言，确切的单位时间是不同的，但是对于算法进行多少个基本操作（即花费多少时间单位）在规模数量级上却是相同的，由此可以忽略机器环境的影响而客观地反应算法的时间效率。

即时间复杂度就是用算法所需的步骤数量来衡量其效率。那么，如何来判定所需步骤数量的标准呢？此时可以使用“大 O 记法”。

大 O 记法

对于算法的时间效率，我们可以用“大 O 记法”来表示，以下从数学上理解：

• 时间复杂度 —— T(n)：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为 T(n)=O(g(n))，则称 O(g(n)) 为算法A的渐近时间复杂度，简称时间复杂度，记为 T(n)。
• “大O记法” —— g(n)：对于单调的整数函数 f，如果存在一个整数函数 g 和实常数 c>0，使得对于充分大的 n，总有 f(n)<=c*g(n)，就说函数 g 是 f 的一个渐近函数（忽略常数），记为 f(n)=O(g(n))。也就是说，在趋向无穷的极限意义下，函数f的增长速度受到函数 g 的约束，亦即函数 f 与函数 g 的特征相似。

通俗理解：当解决问题的计算步骤跟 n 相关时，把旁支末节（次要项和常数项）全部忽略掉，只留下最关键的特征（最高次项），就是大 O 表示法。

以上述引入的示例代码为例：

# 例1：a+b+c=1000，且 a^2+b^2=c^2（a,b,c 为自然数）
for a in range(1001):  # 基本计算步骤为1000次
    for b in range(1001):  # 1000次
        for c in range(1001):  # 1000次
            if a + b + c == 1000 and a**2 + b**2 == c**2:  # 1次
                print("a:{}, b:{}, c:{}".format(a, b, c))  # 1次

# 例2：如果改为 a+b+c=2000，且 a^2+b^2=c^2（a,b,c 为自然数）呢？

简单划分示例中的计算步骤数量：

• 例1：T = 1000 * 1000 * 1000 * 2
• 例2：T = 2000 * 2000 * 2000 * 2 
• 即：T(n) = n * n * n * 2 = n^3 * 2

当使用大 O 计法时，去掉相关系数 2，只会留下 n³，记为 g(n) = n³ 。此时，可说T(n) = g(n)。

因此，即使相关系数有所变化，如T(n) = n * n * n * 2 = n³ * 10，我们也认为两者（n³ * 2 与 n³ * 10）效率“差不多”。

最坏时间复杂度

分析算法时，存在几种可能的考虑：

• 算法完成工作最少需要多少基本操作，即最优时间复杂度。
• 算法完成工作最多需要多少基本操作，即最坏时间复杂度。
• 算法完成工作平均需要多少基本操作，即平均时间复杂度。

对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。

对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。

对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

时间复杂度的几条基本计算规则

1. 基本操作，即只有常数项，认为其时间复杂度为 O(1)。
2. 顺序结构，时间复杂度按加法进行计算。
3. 循环结构，时间复杂度按乘法进行计算。
4. 分支结构，时间复杂度取各分支中的最大值。
5. 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略。
6. 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度。

示例：

for a in range(n):  # 循环
    for b in range(n):  # 循环
        c = 1000 - a - b  # 基本操作
        if a**2 + b**2 == c**2:  # 分支：要么进入分支中的print，要么退出
            print("a:{}, b:{}, c:{}".format(a, b, c))  # 基本操作            

其时间复杂度：T(n)

= n * n * (1 + max(1, 0))

= n² * 2

= O(n²)

算法分析

第一次尝试的算法核心部分

for a in range(0, 1001):
    for b in range(0, 1001):
        for c in range(0, 1001):
            if a**2 + b**2 == c**2 and a+b+c == 1000:
                print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：T(n) = O(n*n*n) = O(n³)

第二次尝试的算法核心部分

for a in range(0, 1001):
    for b in range(0, 1001-a):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：T(n) = O(n*n*(1+1)) = O(n*n) = O(n²)

由此可见，我们尝试的第二种算法要比第一种算法的时间复杂度好得多。

 

3. 常见的时间复杂度

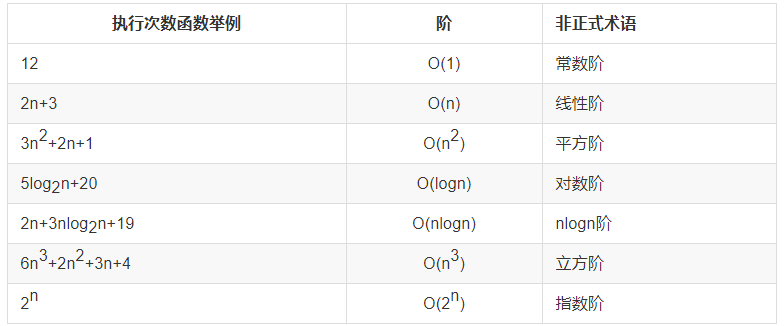
 习惯上将 log₂n （以 2 为底的对数）简写成 logn。

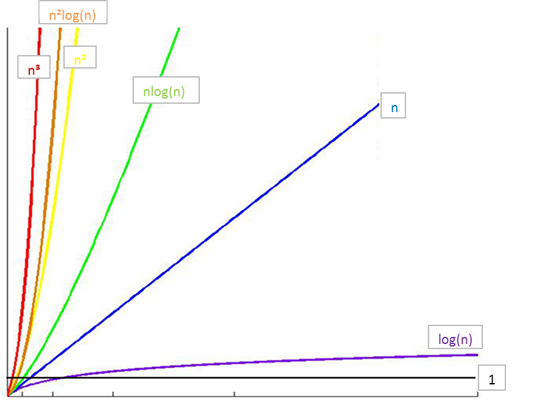
常见时间复杂度之间的关系

 

 

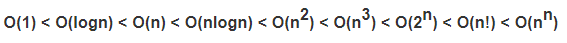
4. Python 内置类型性能分析

timeit 模块

Python3 中的 timeit 模块可以用来测试小段代码的运行时间。其中主要通过两个函数来实现：timeit 和 repeat，代码如下：

def timeit(stmt="pass", setup="pass", timer=default_timer,
           number=default_number, globals=None):
    """Convenience function to create Timer object and call timeit method."""
    return Timer(stmt, setup, timer, globals).timeit(number)

def repeat(stmt="pass", setup="pass", timer=default_timer,
           repeat=default_repeat, number=default_number, globals=None):
    """Convenience function to create Timer object and call repeat method."""
    return Timer(stmt, setup, timer, globals).repeat(repeat, number)

在上面的代码中可见，无论是 timeit 还是 repeat 都是先生成 Timer 对象，然后调用 Timer 对象的 timeit 或 repeat 函数。

在使用 timeit 模块时，可以直接使用 timeit.timeit()、tiemit.repeat()，还可以先用 timeit.Timer() 来生成一个 Timer 对象，然后再用 TImer 对象用 timeit() 和 repeat() 函数，后者再灵活一些。

上述两个函数的入参：

• stmt：用于传入要测试时间的代码，可以直接接受字符串的表达式，也可以接受单个变量，也可以接受函数。传入函数时要把函数申明在当前文件中，然后在 stmt = ‘func()’ 执行函数，然后使用 setup = ‘from __main__ import func’
• setup：传入stmt的运行环境，比如stmt中使用到的参数、变量，要导入的模块等。可以写一行语句，也可以写多行语句，写多行语句时要用分号；隔开语句。
• number：要测试的代码的运行次数，默认 100000 次，对于耗时的代码，运行太多次会比较慢，此时建议自己修改一下运行次数。
• repeat：指测试要重复几次，每次的结果构成列表返回，默认 3 次。

list 的操作测试

import timeit

# ----生成列表的效率----

def t1():
    l = []
    for i in range(1000):
        l = l + [i]

def t2():
    l = []
    for i in range(1000):
        l.append(i)
        
def t3():
    l = [i for i in range(1000)]

def t4():
    l = list(range(1000))


t1 = timeit.timeit("t1()", setup="from __main__ import t1", number=1000)
print("+ used time:{} seconds".format(t1))
print()
t2 = timeit.timeit("t2()", setup="from __main__ import t2", number=1000)
print("append used time:{} seconds".format(t2))
print()
t3 = timeit.timeit("t3()", setup="from __main__ import t3", number=1000)
print("[i for i in range(n)] used time:{} seconds".format(t3))
print()
t4 = timeit.timeit("t4()", setup="from __main__ import t4", number=1000)
print("list(range(n)) used time:{} seconds".format(t4))
print()

# ----pop元素的效率----

x = list(range(1000000))
pop_from_zero = timeit.timeit("x.pop(0)", setup="from __main__ import x", number=1000)
print("pop_from_zero used time:{} seconds".format(pop_from_zero))
print()
x = list(range(1000000))
pop_from_last = timeit.timeit("x.pop()", setup="from __main__ import x", number=1000)
print("pop_from_last used time:{} seconds".format(pop_from_last))

运行结果：

+ used time:3.7056619 seconds

append used time:0.46458129999999986 seconds

[i for i in range(n)] used time:0.18458229999999975 seconds

list(range(n)) used time:0.0845849000000003 seconds

pop_from_zero used time:0.5516430999999997 seconds

pop_from_last used time:0.0002724000000000615 seconds

list 内置操作的时间复杂度

（通过顺序表实现）

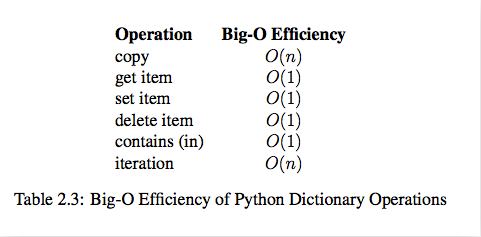
dict 内置操作的时间复杂度

（通过哈希表实现）

 

5. 数据结构

需求：我们如何用 Python 中的类型来保存一个班的学生信息？ 如果想要快速的通过学生姓名获取其信息呢？

实际上当我们在思考这个问题的时候，我们已经用到了数据结构。列表和字典都可以存储一个班的学生信息，但是想要在列表中获取一名同学的信息时，就要遍历这个列表，其（最坏）时间复杂度为 O(n)。而使用字典存储时，可将学生姓名作为字典的键，学生信息作为值，进而查询时不需要遍历便可快速获取到学生信息，其时间复杂度为 O(1)。

我们为了解决问题，需要将数据保存下来，然后根据数据的存储方式来设计算法以实现数据的处理，那么数据的存储方式不同就会导致需要不同的算法进行处理。我们希望算法解决问题的效率越快越好，于是就需要考虑数据究竟如何保存的问题，这就是数据结构。数据结构是为算法服务的，具体选择什么数据结构，与期望支持的算法（操作）有关。

在上面的问题中我们可以选择 Python 中的列表或字典来存储学生信息。列表和字典就是 Python 内建帮我们封装好的两种数据结构。

概念

数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型。如：int，float，char 等。数据元素之间不是独立的，存在特定的关系，这些关系便是结构。数据结构指数据对象中数据元素之间的关系。

Python 给我们提供了很多现成的数据结构类型，这些系统自己定义好的，不需要我们自己去定义的数据结构就叫做 Python 的内置数据结构，比如列表、元组、字典。而有些数据组织方式，Python 系统里面没有直接定义，需要我们自己去定义实现这些数据的组织方式，这些数据组织方式称之为 Python 的扩展数据结构，比如栈，队列等。

算法与数据结构的区别

数据结构只是静态的描述了数据元素之间的关系。

高效的程序需要在数据结构的基础上设计和选择算法。

总结：算法是为了解决实际问题而设计的，数据结构是算法实现的容器。

抽象数据类型（Abstract Data Type）

抽象数据类型（ADT）的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。

引入抽象数据类型的目的是把数据类型的表示和数据类型的运算实现，与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

最常用的数据运算有五种：

• 插入
• 删除
• 修改
• 查找
• 排序