js找出一定范围内的全部素数(埃拉托斯特尼筛法Sieve of Eratosthenes)
最近在看js的基础,看到函数这一章的时候,看到了这种写法。

原文链接:https://zh.javascript.info/function-basics
突然懵了个B,js还能这么写。然后问了下chat,才想起来这是js的标签用法。
在JavaScript中,标签(label)是一种标识符,用于标记代码中的特定位置,通常是在循环语句中使用。标签的主要作用是在嵌套的循环中,让`break`和`continue`等控制流语句能够跳出或者跳过指定的循环,而不是默认地只操作当前内层循环。
语法是一个普通的标识符后面跟一个冒号,例如:`labelName`。
outerLoop: for (let i = 0; i < 3; i++) { for (let j = 0; j < 3; j++) { if (i === 1 && j === 1) { break outerLoop; // 跳出外层循环 } console.log(i, j); } }
当i和j都为1的时候就直接跳出了外层循环。结果就是输出:
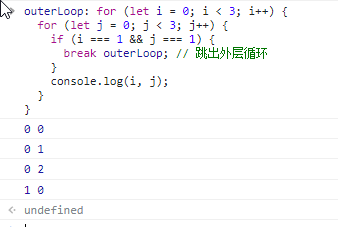
其实这个标签在实际编程中用的并不多,因为会使代码变得难以理解,而且不好维护。
讲了这么多,还没说到本文的重点,那就是埃拉托斯特尼筛法。之所以知道这个方法,是因为我贴第一段代码问chat的时候,chat给我推荐了这个算法。

然后我就google了这个算法。刚开始看代码是不懂这个算法的,直到看到维基百科的这张gif,瞬间就明白了。https://upload.wikimedia.org/wikipedia/commons/thumb/b/b9/Sieve_of_Eratosthenes_animation.gif/350px-Sieve_of_Eratosthenes_animation.gif
它的基本思路是从最小的素数开始,将其倍数标记为非素数,然后继续处理下一个未被标记的数,直到处理完所有小于给定范围的数。
基本步骤如下:
1、首先创建一个长度为`n + 1`的布尔数组`isPrime`,初始时就所有元素设置为`true`,表示所有的数字都是素数。
2、从2开始,遍历到`sqrt(n)`,对于每个数`i`,如果`isPrime[i]`为`true`,则执行下面的步骤:
a.将`i`标记为素数(因为`i`自身是素数)。
b.将大于等于`i`的`i`的倍数标记为非素数。从`i * i`开始,每次增加`i`,直到达到或超过`n`。
3、遍历数组`isPrime`,所有仍然标记为`true`的索引位置即为素数。
这个方法的优势在于它避免了重复检查,一旦某个数标记为非素数,它所有倍数也会标记,从而减少了不必要的计算。
第2部之所以遍历到`sqrt(n)`,是因为一个合数(非素数)x可以表示为两个数的乘积,它必定有一个小于等于sqrt(x)的因子,因为如果两个因子都大于sqrt(x),那么乘积必定大于x。
具体的代码如下:
function findPrime(n) { const isPrime = new Array(n + 1).fill(true); isPrime[0] = isPrime[1] = false; for (let i = 2; i <= Math.sqrt(n); i++) { if (isPrime[i]) { for (let j = i * i; j <= n; j += i) { isPrime[j] = false; } } } const primes = []; for (let i = 2; i <= n; i++) { if (isPrime[i]) { primes.push(i); } } return primes; }
posted on 2023-08-29 13:43 hanguahannibk 阅读(41) 评论(0) 编辑 收藏 举报





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 终于写完轮子一部分:tcp代理 了,记录一下
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理