Matlab复现Floyd算法

Floyd算法适用于APSP(All Pairs Shortest Paths，多源最短路径)，是一种动态规划算法，稠密图效果最佳，边权可正可负。此算法简单有效，由于三重循环结构紧凑，对于稠密图，效率要高于Dijkstra算法，也要高于SPFA算法。

优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。
缺点：时间复杂度比较高O(n^3)，不适合计算大量数据。

算法思想：

Floyd算法是一种在具有正或负边缘权重（但没有负周期）的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度（加权）。

其状态转移方程如下： map[i,j] = min{map[i,k]+map[k,j],map[i,j]}；
map[i,j] 表示i到j的最短距离，k是i到j的中介点，map[n,n] 初值应该为0，或者按照题目意思来做。
当然，如果这条路没有通的话就直接将 map[i,j] 设置为inf

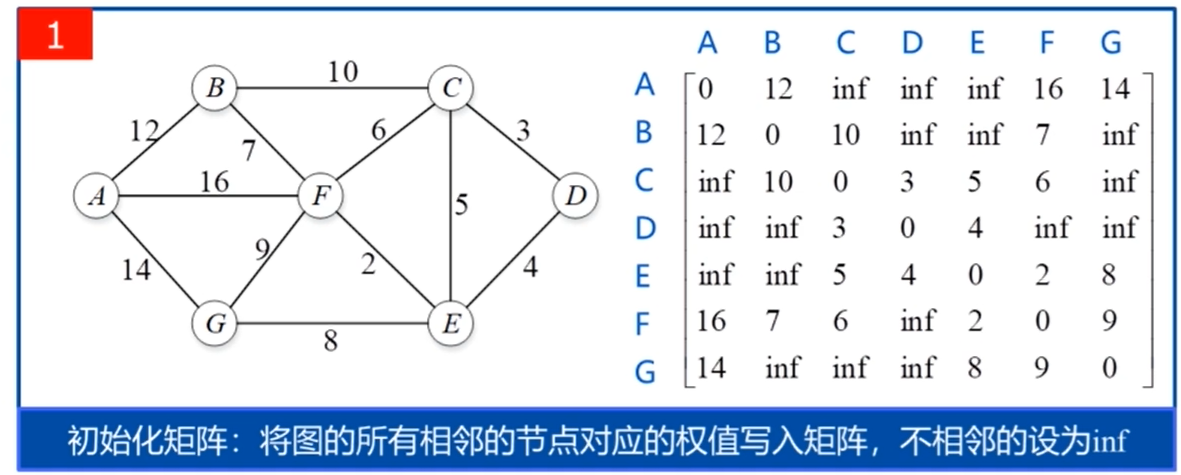
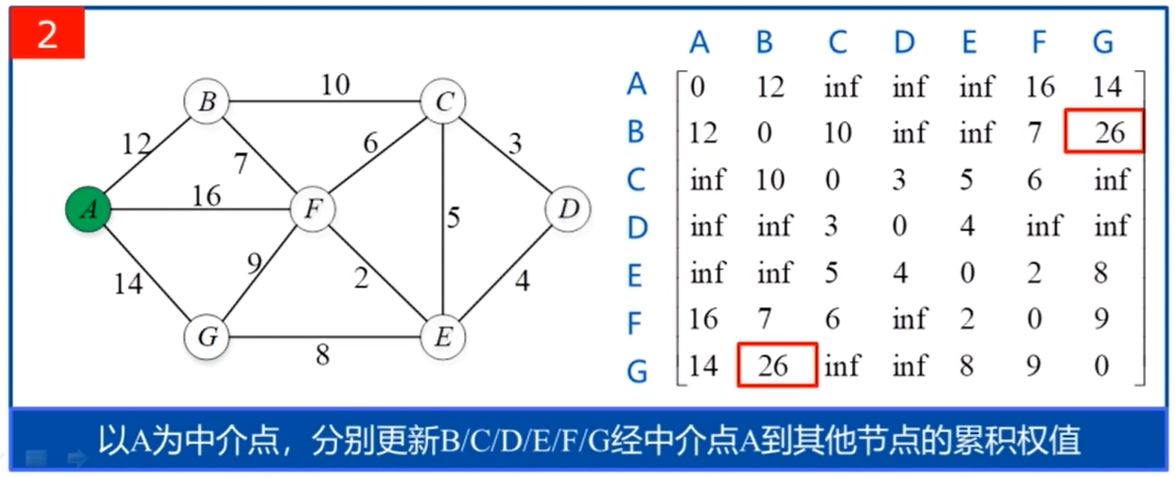
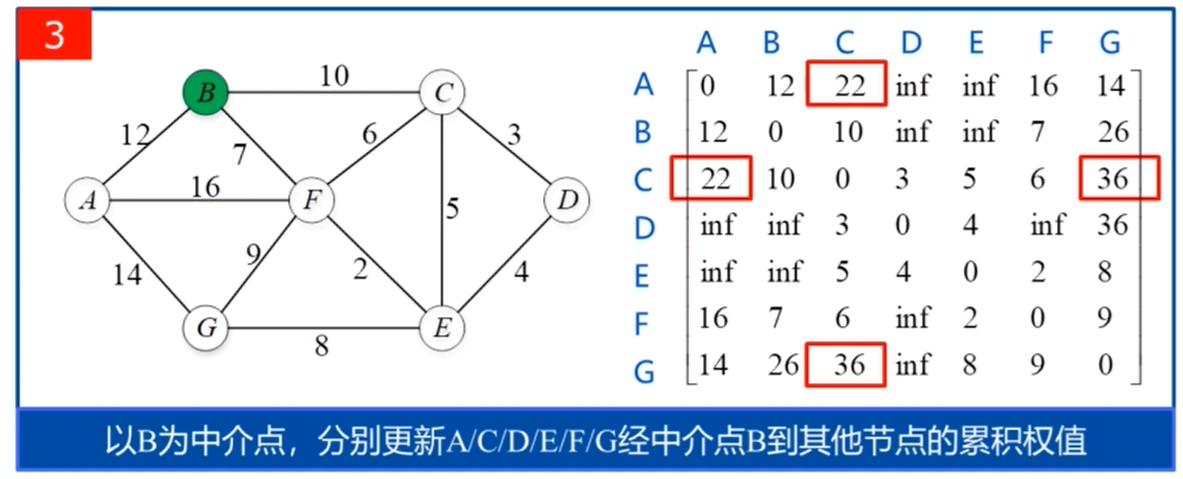
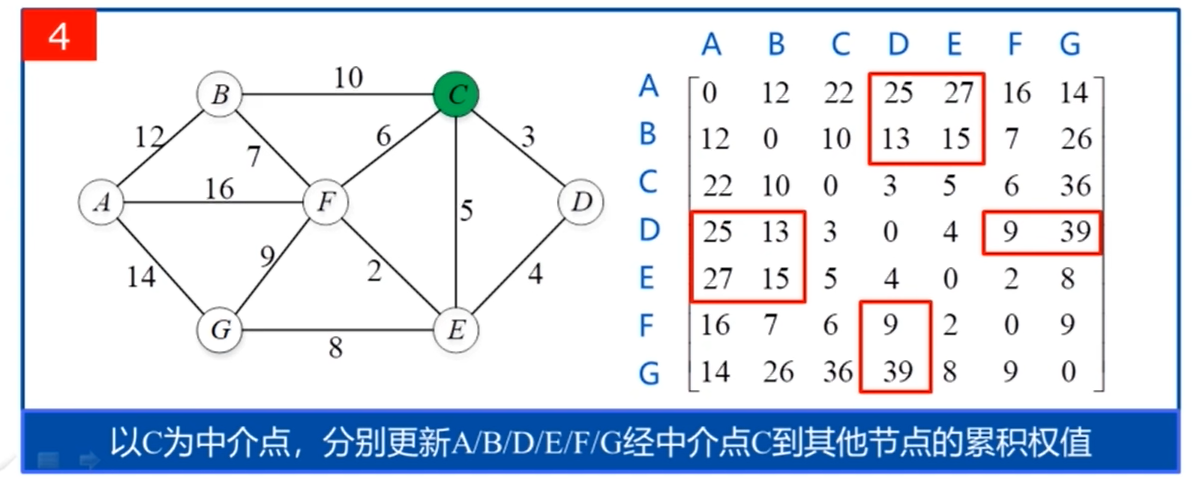
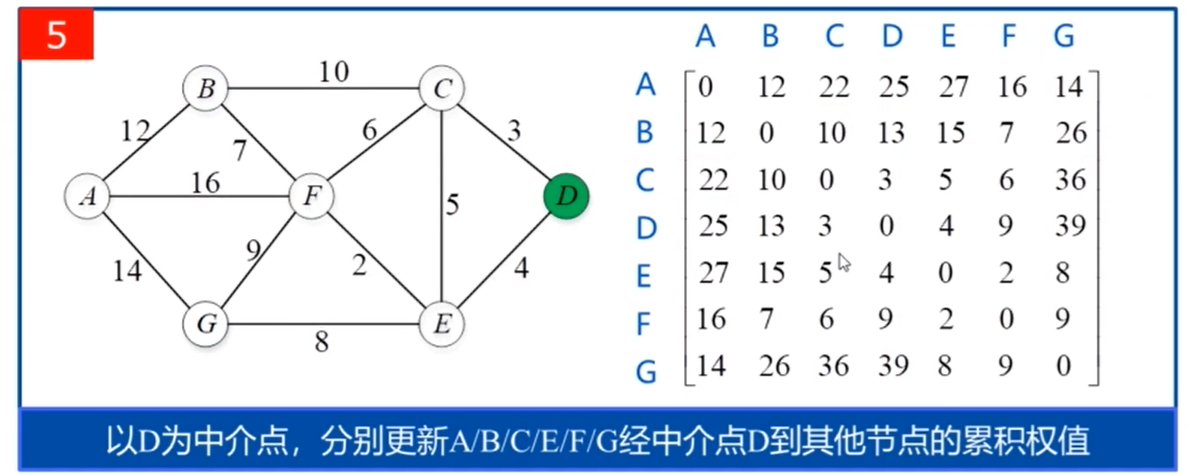
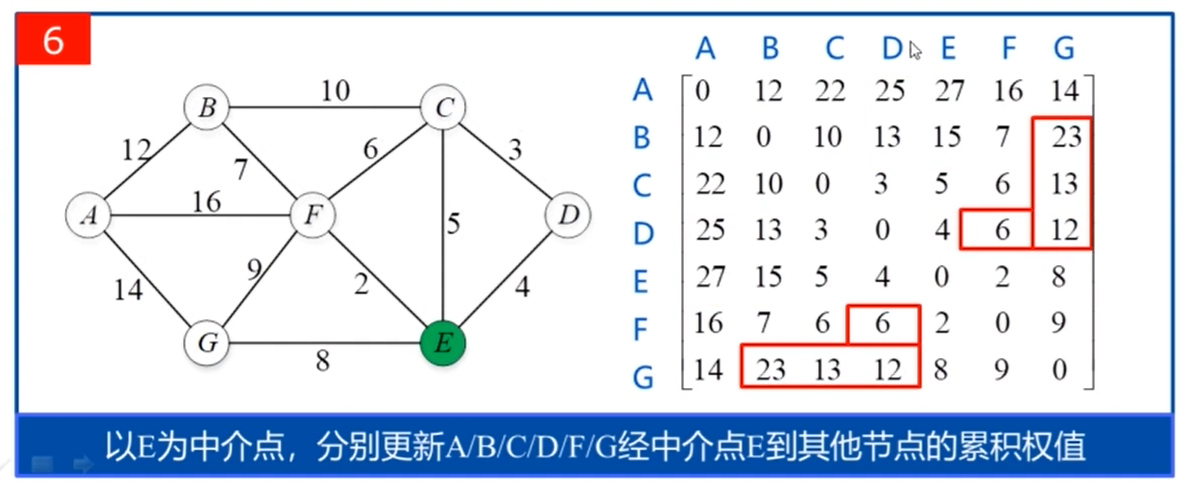
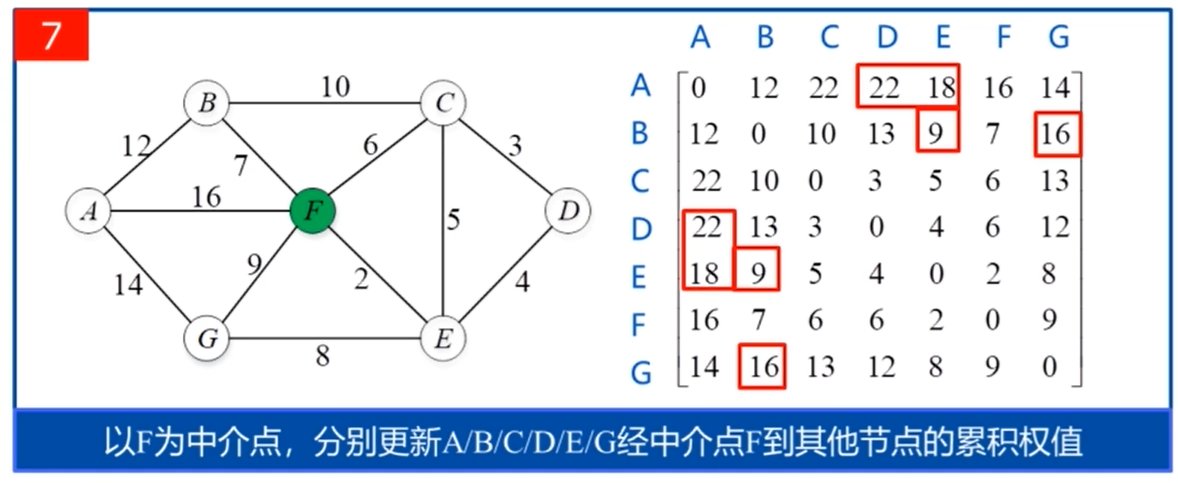
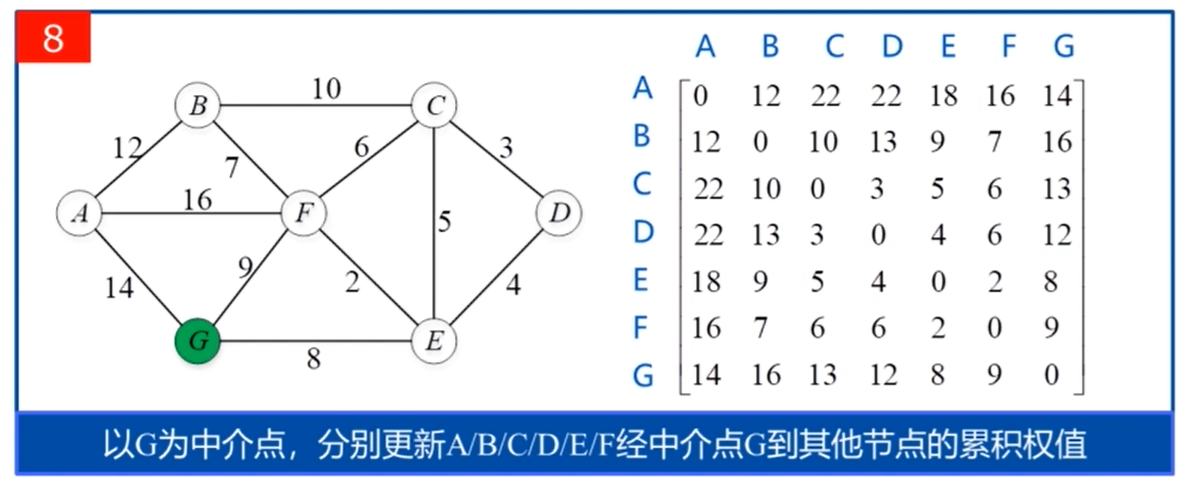
源代码：

init.m：初始化栅格地图

function [field,cmap] = init(rows, cols)
cmap = [1 1 1; ...       % 1-白色-空地
    0 0 0; ...           % 2-黑色-静态障碍
    1 0 0; ...           % 3-红色-动态障碍
    1 1 0;...            % 4-黄色-起始点 
    1 0 1;...            % 5-品红-目标点
    0 1 0; ...           % 6-绿色-到目标点的规划路径   
    0 1 1];              % 7-青色-动态规划的路径

% 构建颜色MAP图
colormap(cmap);

% 定义栅格地图全域，并初始化空白区域
field = ones(rows, cols);

% 障碍物区域
obsRate = 0.3;
obsNum = floor(rows*cols*obsRate);
obsIndex = randi([1,rows*cols],obsNum,1);
field(obsIndex) = 2;

getNeighborNodes.m: 获得给定点的8个邻接点以及距离矩阵

function neighborNodes = getNeighborNodes(rows, cols, lineIndex, field)
[row, col] = ind2sub([rows,cols], lineIndex);
neighborNodes = inf(8,2);


%% 查找当前父节点临近的周围8个子节点
neighborIndex = 1;
for i = -1 : 1
    for j = -1 : 1
        nx = row + i;
        ny = col + j;
        if (i == 0 && j == 0) || nx <= 0 || nx > rows || ny <= 0 || ny > cols
            continue
        end
        child_node_line = sub2ind([rows,cols], nx, ny);
        neighborNodes(neighborIndex,1) = child_node_line;
        if field(nx, ny) ~= 2
            cost = norm([nx, ny] - [row, col]);
            neighborNodes(neighborIndex,2) = cost;
        end
        neighborIndex = neighborIndex + 1;
    end
end

Floyd.m：得到任何两点间的最短路径并存储，将起点到终点的最短路径绘制出来

% 基于栅格地图的机器人路径规划算法
% 第3节：Floyd算法
clc
clear
close all

%% 栅格界面、场景定义
% 行数和列数
rows = 10;
cols = 20;
[field,cmap] = init(rows, cols);

% 起点、终点、障碍物区域
startPos = 3;
goalPos = rows*cols-2;
field(startPos) = 4;
field(goalPos) = 5;

%% 算法初始化
n = rows*cols;      % 栅格节点总个数
map = inf(n,n);     % 所有节点间的距离map, 邻接矩阵
path = cell(n, n);  % 存放对应的路径

% 初始化邻接矩阵和路径矩阵
for startNode = 1:n
    if field(startNode) ~= 2  % 如果不是障碍物
        neighborNodes = getNeighborNodes(rows, cols, startNode, field);
        for i = 1:8
            if ~(isinf(neighborNodes(i,1)) || isinf(neighborNodes(i,2)))
                neighborNode = neighborNodes(i,1);
                map(startNode, neighborNode) = neighborNodes(i,2);
                path{startNode, neighborNode} = [startNode, neighborNode];
            end
        end
    end
end
           
%% 进入三层主循环
for k = 1 : n   % 中介点
    for i =  1 : n
        if i ~= k
            for j =  1 : n
                if j ~= i && j ~= k
                    if map(i,k) +  map(k,j) < map(i,j)
                        map(i,j) = map(i,k) +  map(k,j);
                        path{i,j} = [path{i,k}, path{k,j}(2:end)];
                    end
                end
            end
        end
    end
end


%% 画栅格界面
% 找出目标最优路径
path_target = path{startPos,goalPos};
field(path_target(2:end-1)) = 6;

% 画栅格图
image(1.5,1.5,field);
grid on;
set(gca,'gridline','-','gridcolor','k','linewidth',2,'GridAlpha',0.5);
set(gca,'xtick',1:cols+1,'ytick',1:rows+1);
axis image;

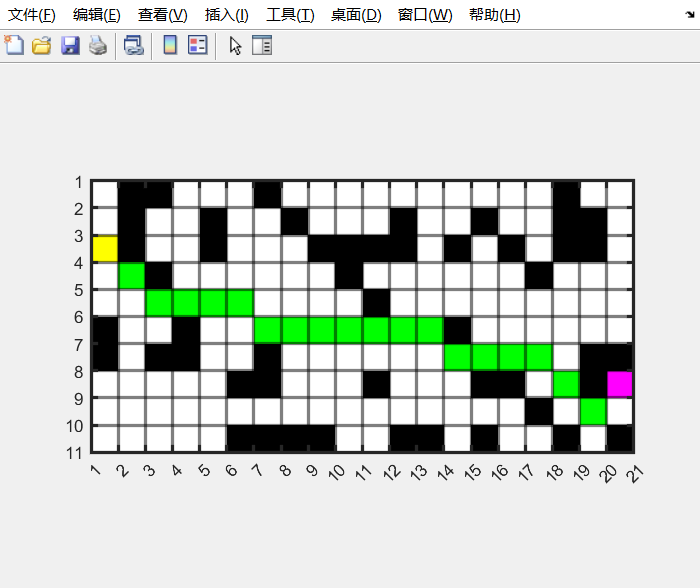
运行结果：

起点到终点的最短路径：

>> path{3,198}

ans =

     3    14    25    35    45    55    66    76    86    96   106   116   126   137   147   157   167   178   189   198

>>