Matlab复现迪杰斯特拉算法

Dijkstra算法可以计算出在有权图中从某个起点出发到其他任何一点的最短路径长度

算法思想：

迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

定义起点s，终点t，集合U表示还没有找到起点到该点的最短路径的点的集合，集合S表示已经找到最短路径的点的集合，初始情况下S集合中只有起点一个点，最短路径是0

假设要求D到A点的最短路径：

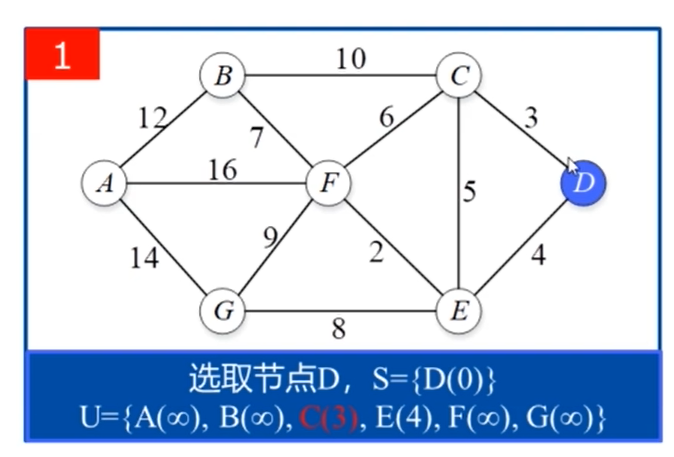
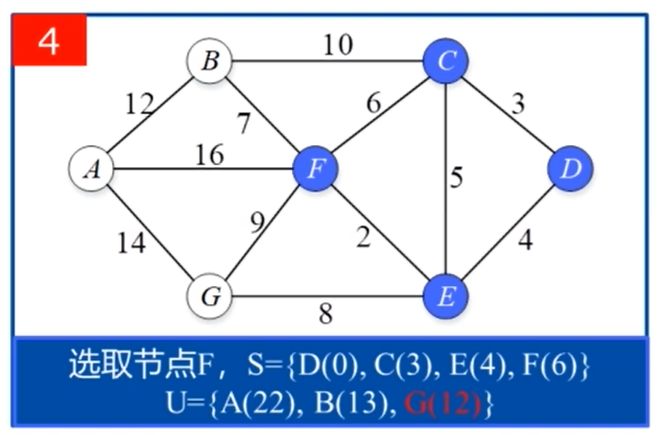
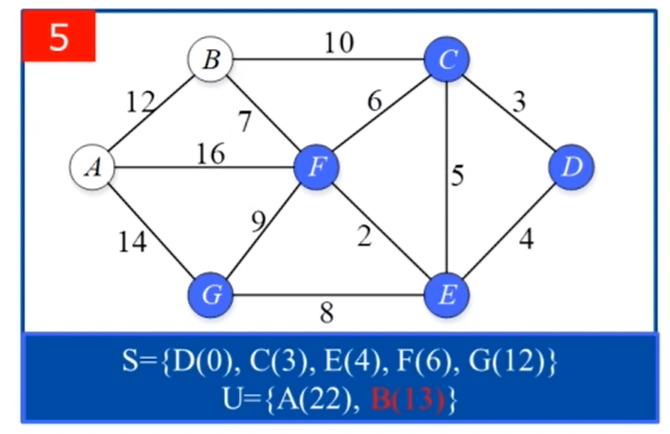
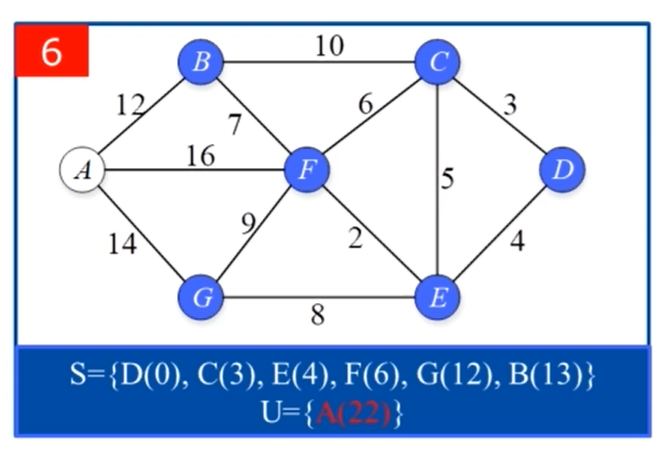
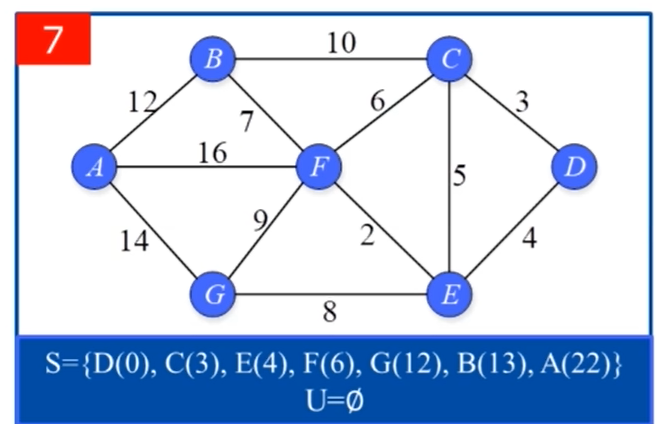
算法实现过程中用到的一些技巧:

• 删除矩阵某一行：

  >> A = [1,2,3;4,5,6;7,8,9]
  
  A =
  
       1     2     3
       4     5     6
       7     8     9
  
  >> A(2,:) = []    % 删除A矩阵的第2行
  
  A =
  
       1     2     3
       7     8     9
  
  >>
  

• 在矩阵末尾添加一行

  A(end+1,:) = [1,2,3]
  

• 枚举某个点相邻的8个节点：

  for i = -1 : 1
      for j = -1 : 1
          nx = x + i;
          ny = y + j;
          if (i == 0 && j == 0) || nx <= 0 || nx > rows || ny <= 0 || ny > cols
              continue
          end
          ......
      end
  end
  

• 使用元胞数组cell存储起点到达每个点的路径

  >> A = {1,2,3;'text',rand(5,10,2),{11; 22; 33}}
  
  A =
  
    2×3 cell 数组
  
      {[   1]}    {[          2]}    {[     3]}
      {'text'}    {5×10×2 double}    {3×1 cell}
  
  >> 
  

源代码：

init.m: 初始化栅格地图

function [field,cmap] = init(rows, cols)
cmap = [1 1 1; ...       % 1-白色-空地
    0 0 0; ...           % 2-黑色-静态障碍
    1 0 0; ...           % 3-红色-动态障碍
    1 1 0;...            % 4-黄色-起始点 
    1 0 1;...            % 5-品红-目标点
    0 1 0; ...           % 6-绿色-到目标点的规划路径   
    0 1 1];              % 7-青色-动态规划的路径

% 构建颜色MAP图
colormap(cmap);

% 定义栅格地图全域，并初始化空白区域
field = ones(rows, cols);

% 障碍物区域
obsRate = 0.3;
obsNum = floor(rows*cols*obsRate);
obsIndex = randi([1,rows*cols],obsNum,1);
field(obsIndex) = 2;

getNeighborNodes.m：获得给定一维索引节点的8个节点以及距离

function neighborNodes = getNeighborNodes(rows, cols, lineIndex, field)
[row, col] = ind2sub([rows,cols], lineIndex);
neighborNodes = inf(8,2);


%% 查找当前父节点临近的周围8个子节点
neighborIndex = 1;
for i = -1 : 1
    for j = -1 : 1
        nx = row + i;
        ny = col + j;
        if (i == 0 && j == 0) || nx <= 0 || nx > rows || ny <= 0 || ny > cols
            continue
        end
        child_node_line = sub2ind([rows,cols], nx, ny);
        neighborNodes(neighborIndex,1) = child_node_line;
        if field(nx, ny) ~= 2
            cost = norm([nx, ny] - [row, col]);
            neighborNodes(neighborIndex,2) = cost;
        end
        neighborIndex = neighborIndex + 1;
    end
end

Dijkstra.m: 得到起点到终点的最短路径并绘制

% 基于栅格地图的机器人路径规划算法
% 第2节：Dijkstra算法
clc
clear
close all

%% 栅格界面、场景定义
% 行数和列数
rows = 10;
cols = 20;
[field,cmap] = init(rows, cols);

% 起点、终点、障碍物区域
startPos = 3;
goalPos = rows*cols-2;
field(startPos) = 4;
field(goalPos) = 5;

%% 算法初始化
% S/U的第一列表示栅格节点线性索引编号
% 对于S，第二列表示从源节点到本节点已求得的最小距离，不再变更；
% 对于U，第二列表示从源节点到本节点暂时求得的最小距离，可能会变更
U(:,1) = (1: rows*cols)';
U(:,2) = inf;
S = [startPos, 0];
U(startPos,:) = [];  % 在U集合中删除起点，表示起点已经得到最短路径0

% 更新起点的邻节点及代价
neighborNodes = getNeighborNodes(rows, cols, startPos, field);  % 获取到起点的所有邻接点
for i = 1:8
    childNode = neighborNodes(i,1); % 邻接点索引
    % 判断该子节点是否存在
    if ~isinf(childNode)
        idx = find(U(:,1) == childNode);
        U(idx,2) = neighborNodes(i,2);
    end
end


% S集合的最优路径集合
for i = 1:rows*cols
    path{i,1} = i;
end
for i = 1:8
    childNode =  neighborNodes(i,1);
    if ~isinf(neighborNodes(i,2))
        path{childNode,2} = [startPos,neighborNodes(i,1)];
    end
end


%% 循环遍历
while ~isempty(U)
    % 在U集合找出当前最小距离值的节点,视为父节点，并移除该节点至S集合中
    [dist_min, idx] = min(U(:,2));
    parentNode = U(idx, 1);
    S(end+1,:) = [parentNode, dist_min];  % 加入S集合中
    U(idx,:) = [];  % 在U集合中删除
    
    % 获得当前节点的临近子节点
    neighborNodes = getNeighborNodes(rows, cols, parentNode, field);

    % 依次遍历邻近子节点，判断是否在U集合中更新邻节点的距离值
    for i = 1:8
        % 需要判断的子节点
        childNode = neighborNodes(i,1);
        cost = neighborNodes(i,2);
        if ~isinf(childNode)  && ~ismember(childNode, S)
            
            % 找出U集合中节点childNode的索引值
            idx_U = find(childNode == U(:,1));            
            
            % 判断是否更新
            if dist_min + cost < U(idx_U, 2)
                U(idx_U, 2) = dist_min + cost;

                % 更新最优路径
                path{childNode, 2} = [path{parentNode, 2}, childNode];
            end
        end
    end
end


%% 画栅格界面
% 找出目标最优路径
path_opt = path{goalPos,2};
field(path_opt(2:end-1)) = 6; % 标记路径

% 画栅格图
image(1.5,1.5,field);
grid on;
set(gca,'gridline','-','gridcolor','k','linewidth',2,'GridAlpha',0.5);
set(gca,'xtick',1:cols+1,'ytick',1:rows+1);
axis image;

运行结果：

绿色表示最短路径: