ABC247 Max Min

题目链接：https://atcoder.jp/contests/abc247/tasks/abc247_e

题目大意是给定一个序列A，X和Y，问序列A中有多少个子区间满足子区间的最大值是X，最小值是Y

方法一：容斥原理

假设get(y,x)表示满足区间中所有数大于等于y且小于等于x的子区间的个数，注意，不一定要保证区间中一定出现y或者x

那么get(y+1,x) 表示在满足get(y,x)的所有子区间中不包含ly子区间的个数, 同理get(y,x-1)表示在满足get(y,x)的所有子区间中不包含x的子区间的个数

get(y+1,x-1) 表示在满足get(y,x)的所有子区间中既不包含y，又不包含x的子区间的个数

我们要求的是必须同时包含y和x的子区间的数目,根据容斥原理：

答案 = 所有区间数 - 不包含X的区间数 - 不包含Y的区间数 + 既不包含X又不包含Y的区间数 get(y,x) - get(y+1,x) - get(y,x-1) + get(y+1,x-1)

那么如何求get(y,x) 呢：我们知道get(y,x) 统计的所有区间都是不包含小于y的数和大于x的数的，所以我们可以在原序列A中用小于y的数或者大于x的数将序列分成若干段，每一段都是符合条件的区间，我们只需要在分割的每个子区间内求区间数量之和即可

用以下样例举例：

5 2 1
1 3 2 4 1

//n = 5, x = 2, y = 1

将序列 {1 3 2 4 1} 进行划分：

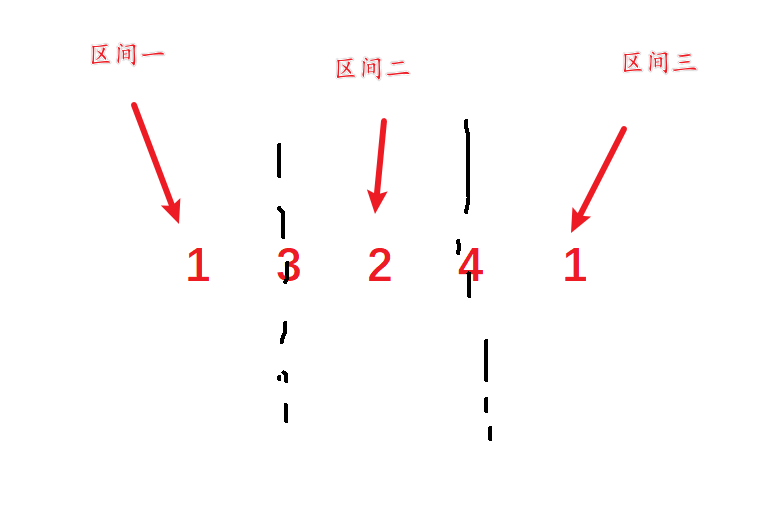
这样可以划分成三个子区间, 每个子区间都满足所有数都在y和x之间（包括x和y）

那么问题就转换成了求给定一个区间求有多少个子区间，这里有个公式，假设区间长度为n， 则子区间个数 = n*(n+1)/2

公式证明：

枚举左端点，对于每个固定的左端点找到右端点的个数，比如 以第一个点为左端点的子区间的个数为：n，以第二个点为左端点的子区间个数为n-1,

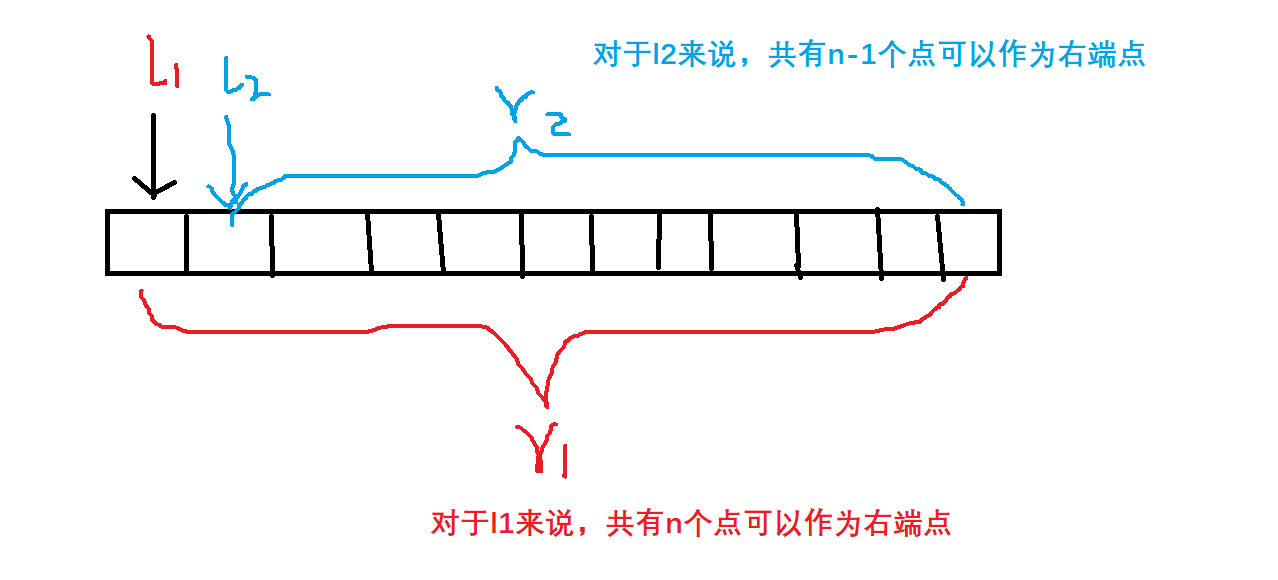
... 以第n个点为左端点的区间个数为1

将以上的所有情况相加：n + (n-1) + (n-2) + ... + 1 = n * (n+1) / 2 //等差数列求和

最后根据前面的容斥原理得出答案

代码：

#include <bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i = a;i < b;i++)
#define per(i,a,b) for(int i = b - 1;i >= a;i--)
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
typedef long long ll;
typedef pair<int,int> PII;
typedef vector<int> VI;

const int N = 200010;
int a[N], n, x, y;

ll get(int l,int r) {
    ll res = 0, cnt = 0;
    rep(i,0,n) {
        if(a[i] < l || a[i] > r) res += 1ll * cnt * (cnt + 1) / 2, cnt = 0;
        else cnt++;
    }
    if(cnt) res += 1ll * cnt * (cnt + 1) / 2;
    return res;
}

int main() {
    scanf("%d%d%d", &n, &x, &y);
    rep(i,0,n) scanf("%d", &a[i]);
    printf("%lld\n", get(y,x) - get(y+1,x) - get(y,x-1) + get(y+1,x-1));
    return 0;
}

方法二：双指针:

和上一个方法一样，也是将区间进行划分，不同的是，我们是直接求每个子区间中满足条件的区间数量（不再统计全部）

这样对于每个子区间的统计就可以用双指针来做，具体看代码

代码：

#include <bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i = a;i < b;i++)
#define per(i,a,b) for(int i = b - 1;i >= a;i--)
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
typedef long long ll;
typedef pair<int,int> PII;
typedef vector<int> VI;

const int N = 200010;
int n, x, y, idx;
VI v[N];


int main() {
    scanf("%d%d%d", &n, &x, &y);
    //最大值是x，最小值是y
    //将每一段子区间都放到一个vector中
    rep(i,0,n) {
        int xx;
        scanf("%d", &xx);
        if(xx < y || xx > x) {
            if(v[idx].size() != 0)
                idx++;
        }
        else v[idx].push_back(xx); 
    }

    ll res = 0;

    rep(i,0,idx+1) {
        unordered_map<int,int> hs;  //开哈希表用来统计是否出现x和y
        for(int j = 0, k = 0;j < (int)v[i].size();j++) {
            while((hs[x] == 0 || hs[y] == 0) && k < (int)v[i].size()) {
                hs[v[i][k]]++;
                k++;
            }
            if(hs[x] != 0 && hs[y] != 0) res += (int)v[i].size() - k + 1;  //此时以k和这个区间末尾之间的所有位置都可以作为以j位置为左端点区间的右端点
            hs[v[i][j]]--;  //j右移一位，将这个位置的数值从哈希表中移除
        }
    }

    printf("%lld\n", res);
    return 0;
}