leetCode1104. 二叉树寻路(medium)

审题：

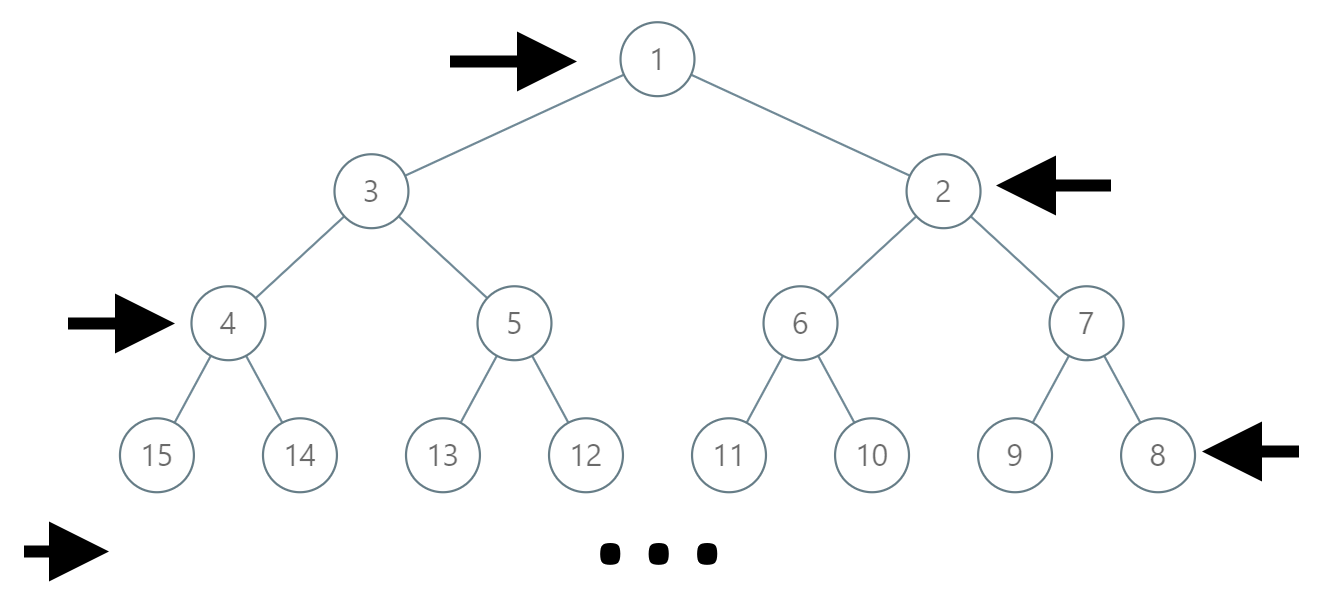
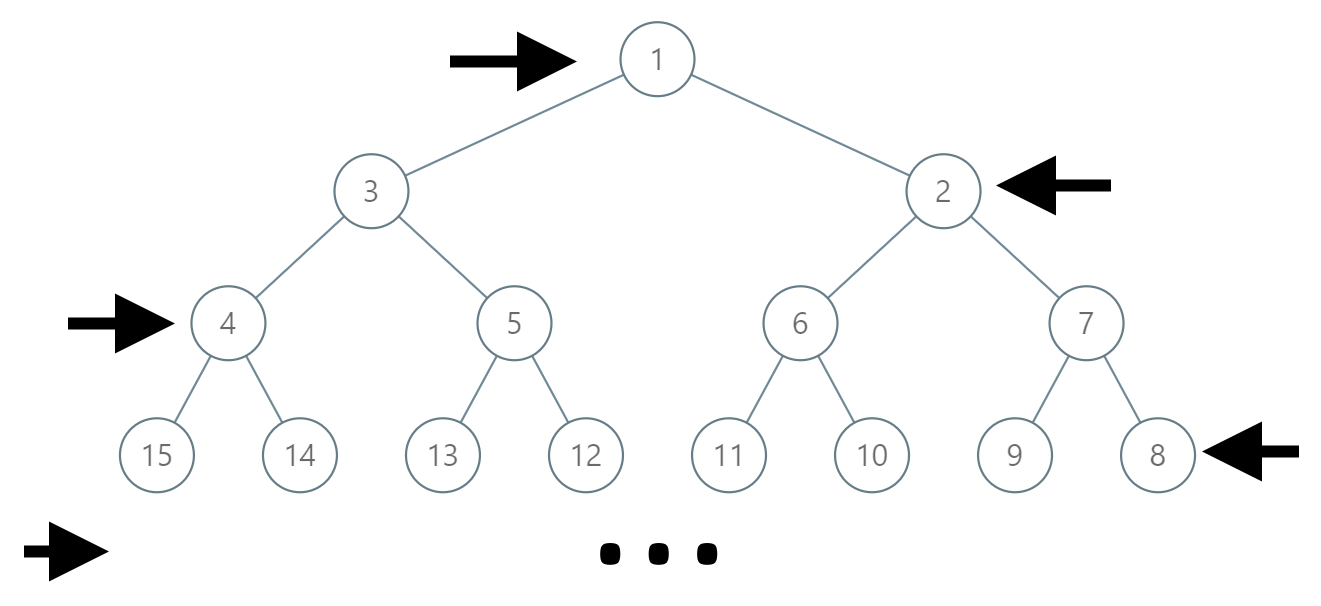
在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

来源：力扣（LeetCode）
读完题，会发现其实和二叉树没多大关系，只是为了将一个数据进行一分为二，第二行的数据倒过来排序，一道数学题。我们要输出的就是根节点到当前叶子节点的一条路径！

思考：

发现只要将给出的叶子节点，然后一直找父节点，最后找到根节点，然后逆序输出就是想要的结果，这个过程我们可以写成一个递归。

核心就是如何根据子节点的值找到父节点的值，找规律，会发现第一行最大值为1，第二行最大值为3，第三行最大值为7，会发现为(2^n)-1,

最小值就是2^(n-1)。此时我们可以计算出n,也是这棵树的深度。然后计算出偏移量，就可以得到父节点的值！下面贴代码和注释：

        public List<Integer> pathInZigZagTree(int label) {
            List<Integer> li = new ArrayList<>();
            fuf(label, li);
            return li;

        }

        /**
         * 进行递归
         */
        int fuf(int s, List<Integer> t) {
            // 找到了根节点，退出递归
            if (s <= 1) {
                t.add(s);
                return s;
            }
            // 求出父亲
            int f = fuf(s);
            int a = fuf(f, t);
            // 回归的时候进行添加，这样不用逆序
            t.add(s);
            return a;
        }

        /**
         *
         * @param s 当前节点值
         * @return 父亲节点值
         */
        int fuf(int s) {
            double a = Math.log((double) (s + 1)) / Math.log((double) 2);
            int d = 0;
            // 算出深度，
            if (a > (int) a) d = (int) a + 1;
            else d = (int) a;
            // 最小节点的值
            int L = (int) Math.pow(2, d - 1);
            // 偏移量
            int len = s - L;
            // 父亲节点的偏移量
            int g = len / 2;
            return L - 1 - g;
        }