Notes of Machine Learning (Stanford), Week 1~2, Linear Regression
①假设函数(hypothesis function)
在给定一些样本数据(training set)后，采用某种学习算法(learning algorithm)对样本数据进行训练，得到了一个模型或者说是假设函数。
当需要预测新数据的结果时，将新数据作为假设函数的输入，假设函数计算后得到结果，这个结果就作为预测值。
假设函数的表示形式一般如下：θ 称为模型的参数(或者是：权重weights)，x就是输入变量(input variables or feature variables)
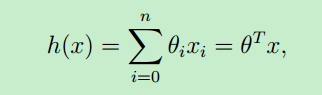
可以看出，假设函数h(x)是关于x的函数，只要确定了 θ ，就求得了假设函数 (θ 也可视为一个向量)。那么对于新的输入样本x，就可以预测该样本的结果y了。
上面假设函数是从0到n求和，也就是说：对于每个输入样本x，将它看成一个向量，每个x中有n+1个 features。比如预测房价，那输入的样本 x(房子的大小，房子所在的城市，卫生间个数，阳台个数.....一系列的特征)
关于分类问题和回归问题：假设函数的输出结果y（predicted y）有两种表示形式：离散的值和连续的值。比如本文中讲到的预测利润，这个结果就是属于连续的值；再比如说根据历史的天气情况预测明天的天气（下雨 or 不下雨），那预测的结果就是离散的值(discrete values)
因此，若hypothesis function输出是连续的值，则称这类学习问题为回归问题(regression problem)，若输出是离散的值，则称为分类问题(classification problem)
②代价函数(cost function)
学习过程就是确定假设函数的过程，或者说是：求出 θ 的过程。
现在先假设 θ 已经求出来了，就需要判断求得的这个假设函数到底好不好？它与实际值的偏差是多少？因此，就用代价函数来评估。
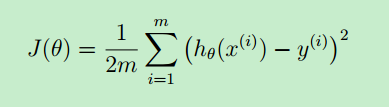
向量化后的代价函数：
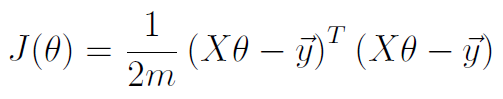
一般地，用 m 来表示训练样本的数目(size of training set)，x(i) 表示第 i 个样本，y(i) 表示第i个样本的预测结果。
从上图可看出：代价函数与“最小均方差”的理念非常相似。J(θ)是 θ 函数。
显然，“代价函数越小，模型就越好”。因此，目标就是：找到一组合适的 θ ，使得代价函数取最小值。
如果我们找到了 θ ，那不就求得了 假设函数了？也就求得一个模型--linear regression model.
那如何找 θ 呢？就是下面提到的梯度下降算法(gradient descent algorithm)
③梯度下降算法(Gradient descent algorithm)
梯度下降算法的本质就是求偏导数，令偏导数等于0，解出 θ
首先从一个初始 θ 开始，然后 for 循环执行上面公式，当偏导数等于0时，θj 就不会再更新了，此时就得到一个最终θj 值。
整个偏导数的运算过程如下：
④假设函数、代价函数和梯度下降算法的向量表示
假设函数的向量表示如下：
代价函数的表示如下：
使用梯度下降算法求解 θ 的向量化表示如下：
（原文上图的式子有一处错误，第一个等号后的式子不应除以m，这里加以更正了）
证明过程如下：
补充：
θ的闭式解（close-form solution）
θ的闭式解也就是它的解析解，就是使得代价函数J(θ)取得最小值的解；
使用闭式解的优点是一步得到精确解，避免了“loop until converge”；
缺点是当特征数量较多时，X的维度较大，而求解的复杂度为O(n^3)，时间代价较高。（特征数量一般以10^4为分界点，高于这个值一般考虑用梯度下降）
引用原文：http://www.cnblogs.com/hapjin/p/6079012.html
