小波变换
1 小波产生的背景与历史
1.0 小波历史简介
1.0.1 傅立叶分析的发展历程
(一) 傅里叶变换 FT
1807年,法国学者Fourier指出任何周期函数都可以用一系列正弦波来表示,开创了傅立叶分析。
-
(1) 操作过程
从数学角度而言,对一个函数进行傅立叶变换(Fourier Transform,FT)。从信号处理的角度而言,对任意信号f(t)的频谱F(w)进行分析。 -
(2) 优点
能够准确刻画平稳信号在整个时(空)域的频率性质。 -
(3) 缺点
不能反映非平稳信号在局部区域的频域特征及其对应关系,即FT在时域没有任何分辨率,无法确定信号奇异性的位置。
(二) 短时傅里叶变换 STFT
1946年,Gabor提出了短时傅立叶变换(Short Time Fourier Transform, STFT)。
-
(1) 操作过程
对信号进行加窗,再对加窗后的信号进行傅立叶变换,从而得到信号在局部区域的频谱。 -
(2) 优点
能够分析信号局部频域特征。 -
(3) 缺点
由于STFT中时间窗的宽度与频率无关,它仍然是一种恒分辨率分析。
(三) 维格纳-威尔分布 WVD
1948年,Ville提出了维格纳-威尔分布(Wigner-Ville Distribution, WVD),并引入时频信号分析。
-
(1) 操作过程
信号中心协方差函数的傅立叶变换。 -
(2) 优点
具有对称性、时移不变性、真边缘性、平均瞬时频率等优良性质,WVD的时频分辨率比STFT的分辨率高。 -
(3) 缺点
存在交叉干扰项(Cross-Term Interference, CTI),这是二次型时频分布的固有结果,大量的CTI会淹没或严重干扰信号的自项,模糊信号的原始特征。
1.0.2 小波分析的发展历程
(一) Haar小波分析
1910年,Haar提出了
-
(1) 操作过程
Haar正交基是以一个简单的二值函数作为母小波经平移和伸缩而形成的。 -
(2) 优点
Haar小波变换具有最优的时(空)域分辨率。 -
(3) 缺点
Haar小波基是非连续函数,因而Haar小波变换的频域分辨率非常差。 -
1936年,Littlewood和Paley对傅立叶级数建立了二进制频率分量分组理论,(即L-P理论:按二进制频率成分分组,其傅立叶变换的相位并不影响函数的大小和形状),这是多尺度分析思想的最早起源;
-
1952年~1962年,Calderon等人将L-P理论推广到高维,建立了奇异积分算子理论;
-
1965年,Calderon发现了著名的再生公式,给出了抛物型空间上H1的原子分解;
-
1974年,Coifman实现了对一维空间和高维空间的原子分解;
-
1976年,Peetre在用L-P理论对Besov空间进行统一描述的同时,给出了Besov空间的一组基;
-
1981年,Stromberg引入了Sobolev空间HP的正交基,对Haar正交基进行了改造,证明了小波函数的存在性。
-
1981年,法国地球物理学家Morlet提出了小波的正式概念;
-
1985年,法国数学家Meyer提出了连续小波的容许性条件及其重构公式。
-
1986年,Meyer在证明不可能存在同时在时频域都具有一定正则性(即光滑性)的正交小波基时,意外发现具有一定衰减性的光滑性函数以构造L2(R)的规范正交基(即Meyer基),从而证明了正交小波系的存在。
-
1984年~1988年,Meyer、Battle和Lemarie分别给出了具有快速衰减特性的小波基函数:Meyer小波、Battle-Lemarie样条小波。
(二) Mallat算法
1987年,Mallat将计算机视觉领域中的多尺度分析思想引入到小波分析中,提出了多分辨率分析的概念,统一了在此前的所有具体正交小波的构造,给出了构造正交小波基的一般方法,提出了快速小波变换(即Mallat算法)。它标志着第—代小波的开始?
-
(1) 操作过程
先滤波,再进行抽二采样。 -
(2) 优点
Mallat算法在小波分析中的地位相当于FFT在经典傅立叶分析中的地位。它是小波分析从纯理论走向实际应用。 -
(3) 缺点
以傅立叶变换为基础,直接在时(空)域中设计滤波器比较困难,并且计算量大。 -
1988年,Daubechies基于多项式方式构造出具有有限支集的光滑正交小波基(即Daubechies基)。
-
1992年,Daubechies对这些演讲内容进行了总结和扩展形成了小波领域的经典著作——小波十讲《Ten Lectures on Wavelet》。
-
1992年3月,国际权威杂志《IEEE Transactions on Information Theory》专门出版了“小波分析及其应用”专刊,全面介绍了此前的小波分析理论和应用及其在不同学科领域的发展,从此小波分析开始进入了全面应用阶段。
-
1992年,Kovacevic和Vetterli提出了双正交小波的概念。
1992年,Cohen、Daubechies和Feauveau构造出具有对称性、紧支撑、消失矩、正则性等性质的双正交小波。
-
(1) 操作过程
利用两组互为对偶的尺度函数和小波函数实现函数的分解与重构。 -
(2) 优点
具有正交小波无法同时满足的对称性、紧支撑、消失矩、正则性等性质。
(三) 小波包(Wavelet Packet, WP)分析
1992年,Coifman和Wickerhauser提出了小波包 (Wavelet Packet,WP)分析。
-
(1) 操作过程
不仅对低通子带进行分解,而且也对高通分量分解,从而聚焦到感兴趣的任意频段。 -
(2) 优点
突破了小波分析对信号频带进行等Q划分的局限性。 -
(3) 缺点
最优基的搜索问题。
(四) 多带小波
1992年,Zou等提出了多带小波(M-band Wavelet)理论,将人们对小波变换的研究从“二带"推广到“多带”情况。
基于“二带”小波变换的多分辨率分析中,尺度函数对应一个低通滤波器,而小波函数对应一个高通滤波器。“二带”小波变换把信号分解成不同的通道,而这些通道的带宽相对于尺度函数的对数是相同的,因此高频通道具有较宽的带宽,而低频通道具有较窄的带宽。
参考链接1:小波变换的优缺点发展历程与时频分析
1.1 “点”的概念
1.1.1 表达“点”的方式
一维中,“点”可以表示为“一个数
我们不可能把空间中的“点/向量”全部表示出来,因此在线性代数中便引入了基的概念,简单来说,基所蕴含的哲学思想就是:
(一) 平凡基
所谓平凡基,就是空间中一些特殊的点/向量,具体表示形式如下:
在这组基下,空间中任意一个点可以表示为:
这样便将“点的差异”
此时,可能会有两个小问题:① 在某些问题中,若是这种基表达不方便/不合适怎么办;② 若是面对的是连续的形式,那么又该如何处理呢?
首先,第一个小问题:在现有的知识范围内,对一类科学问题,可以线性代数的方式来处理。比如数字信号存储中设计的信号压缩,压缩的方法有很多,若是要求线性压缩,也就意味着把数字信号向量经过线性变换,使得线性变换之后的结果更便于存储。考虑一种简单的情况,就是可以通过变换基的形式,使得信号的表达更加简单:
两组基之间的变换矩阵是一个可逆矩阵。
如何理解/解释正交矩阵矩阵呢,
这是代数上的形式,另一方面,正交矩阵也可以理解为:把一组标准正交基变成另一组标准正交基的矩阵,反过来一个线性空间的两个标准正交基之间的过渡矩阵就是正交矩阵。
平凡基的连续形式为冲激函数
。
1.1.2 更复杂的“点”
(一) “点” = 一个数列
这个数列有两种形式:
-
数列的左边固定,右边可以无穷延伸;
-
数列的两边均是无穷延伸的。
此时点可以称为“可数无穷稳定点”。这类点中最典型的就是:
这个点要有一定限制,要求满足如下条件:
类似于要求信号的能量有限。
(二) “点” = 一个函数
有这么一个空间,空间中有很多很多的点,每个点都代表一个函数,这样说其实有点难以理解(或者说难以建立几何直观),这里老师提供了一种一直思路,如下图所示:

上面由离散变为连续是将离散间隔变为无穷小,当然目前我理解这只是一种比较形象的几何示意。
点表示一个函数,又可以分为两类,一种是“周期函数”,另一种是“非周期函数”。
- 周期函数
把所有这类函数记为:
- 非周期函数
可以将非周期函数视为周期为无穷大的周期函数,此时只需要满足:
把这类函数记为:
1.2 傅里叶分析
1807年,傅里叶在论文中指出,任何周期函数,都可以表示为:
该式蕴含了两个优秀的思想:
-
① 从表达的形式来说,不同函数(或者说空间中不同点)的差异转换到系数上;
-
② 对函数/信号的分析,可以通过变换不同的基进行分析。
后来,经过进一步拓展,最终提出了大名鼎鼎的傅里叶变换,对于非周期函数
1910年,科学家Haar构造了一个特殊的函数:
在这个函数基础上,Haar提出了:
这样相当于在给定函数
此时,
这个成果在当时没有引起很大的“浪花”,直到1980年代,地震勘探专家Morlet把短时傅里叶变换(又称加窗傅里叶变换,STFT)进行了修改。
1946年,Gabor提出的STFT的表达形式为:
其表示的含义可概述为:原始信号
逆STFT变换为:
STFT的结果已经很好了,但是人们还是发现了不足之处——窗
因此小波的方法就提出来了(1980年),小波把
2 小波的基础知识
2.1 信号空间
小波中使用的线性空间主要有两个:
- 周期为
- 非周期的能量有限的信号全体:
2.2
(一) 线性性质
取
(二) 内积的概念
(三) 模长或范数
有了这些性质,可将
2.3
2.3.1 FT与IFT变换
FT可以看作是
谱分析:在指定的频率上有多少能量,一个信号的能量沿着不同的频率的分布情况(Ps:也可以参考张颢老师的关于谱分析的解释)。
2.3.2 FT的性质
(一) Parseval Relation(保内积、能量守恒)
(二) 时域与频域的对偶
其中,
这种对偶关系一线性代数的观念来看,就是卷积算子在傅里叶基之下被对角化了。
2.3.3 FT存在的不足
(1) 傅里叶变换对局部的分析或者说局部产生突变时无法分析。
这一点可以从FT的基函数来形象解释,当
固定时,基 是一个幅度不变、周期不变、时间从 到 一直无穷延续的函数,这就意味着如果信号 存在一个频率为 的频率成分,则从 到 一直存在,并且在任何局部的地方不会发生变化。 此外,FT还存在一个很奇怪的点,即信号
是属于 空间的,基函数 却不在 空间中,但是它们还可以作用并得到有意义的结果。
(2) FT结果产生微小扰动时,IFT的结果会产生很大的偏差。
总之,傅里叶变化将信号分的太细了,以至于不同信号之间的区分界限变得很模糊,反而不利于分析。
Ps:关于这一点,老师给了一个“猪肉馅”和“人肉馅”的例子,帮助形象理解,具体参考第06讲 20:00分钟。
因此,若想要改进FT这个工具,一种改进方向就是换基,选择一组更好的基。下面就要介绍一下小波基。
2.4 小波
2.4.1 小波的基本定义
满足如下两个条件就可以称为小波:
-
①
-
② 要求其容许参数满足:
则称
有了小波母函数,则对
其中,称
2.4.2 小波几点注解
(一)
(二)
为了证明上述结论,这里做一点额外的假设(当然也会导致证明不是那么严谨):设
再结合容许参数的要求,就可以证明上述结论了。
(三)
首先,看一下特殊情况,此时
- 尺度

- 尺度

在FT变换中,频率
- 位移
就是进行左右平移了。
2.4.3 小波变换
(一) 小波变换基本定义
对于任意一个信号
上面就是对信号进行小波变换的形式。
由表达式可以看到,小波变换把一维的信号
其他的“升维分析”的例子:支持向量机SVM、神经网络。
(二) 小波变换的基本性质
- 小波变换的Parseval Relation(能量守恒)
展开其具体形式为:
其中,
- 范数守恒
一般
- 逆小波变换
根据逆小波变换的表达式可以看到,当
注释1:令
,则逆小波变换就是“ ”,这里之所以打上了引号,是因为运行存在不相等的点,但是这些点不是很多,把这些不相等的点组成一个点集,要求这个点集的长度等于0,其实这里表达是几乎处处相等,具体可以参考测度论/泛函分析/实分析的内容。(Ps:第9讲 09:00分钟)
但是,当, 是连续的时候, 。
注释2:在
空间中,信号能量都是有限的,即 ,而若 能被拿过来进行积分考察能量是否有限,需要保证 是处处连续的,否则这个积分都没法积。因此注释1和2联立在一起,则能保证小波变换数值相等。
注释3:测度——
,可以看到由于分母存在 项,导致 很小(对应于高频)时, 获得的权重越大, 很大(对应于低频)时, 获得的权重越小,越不重要。因此对信号的小波分析,主要集中在 较小的部分进行分析。
3 小波变换的基本理论
3.1 吸收/对称小波
所谓“吸收分析”就是将
如果上式是成立的,则对应的小波
- Parseval Relation(能量守恒)
- 范数守恒
- 逆小波变换
3.2 二进小波
对小波函数本身施加更加严格的条件/限制,使得它对信号
其中,
- 逆二进小波变换
其中,
上式同样只需要满足几乎处处即可,称
小节:
用于分解,进行小波正变换, 用于重构,做小波逆变换。
如何找到对应
此时
3.3 正交小波
尺度参数
若
构成O.N.B),则称
这个条件已经算是相当苛刻了,在该约束条件下相当于:
此时,在正交小波的形式下,其逆变换为:
其中,
也就是:
4 多分辨分析(正交小波分析)和小波构造
4.1 正交小波分析
4.1.1 常见的正交小波
(一) Haar小波
由Haar小波离散化得到的:
构成
之后,若能进一步验证
(二) 香农小波
下面将借助香农采样定理作为一个桥梁,试图找到
- 香农采样定理
对于
则有(
其中,采样间隔需要满足:
|
考察特殊情况1: 其中, 下面验证是否有如下表达式成立,若成立,则 将内积展开: 也即得到了验证;此时,满足此条件的信号空间为: 总上, |
由这2个特殊情况做进一步拓展:若让
这里解释一下
在此空间中表示:
根据傅里叶变换是一个酉变换可得:
形象化的理解证明请参考课程第14讲 22:00分钟。
正交基的逼近:
不加证明,取个特例
可以看到最终取极限的结果是冲激函数
通过如此复杂的分析,却没得到有意义的结果。
那么这里出现什么问题了呢?(具体的、深刻的、内在的、本质的原因我暂时还说不出来,也听不太懂)老师最后说:
做研究迷茫了、发现结果跟预想的不一样了,可以试着回到出发点看看一开始是不是就发生了错误,或者可以试试逆着往回推导,看看能不能发现不正确的地方。
设任给一个
O.N.S,由这个O.N.S作为一个O.N.B生成一个线性子空间,这里将其记为
上式的意思是,把
小结:
就是以 这组 O.N.S为O.N.B构成的线性子空间。
下面考察
- ① 当
根据这条性质,可以判断
- ② 由于
- ③
考察几个特例:
- ④ 根据第③条结论,可以得到
综上,两种方式逼近


那么
通过取几个特例容易验证,
这样看来,
之后我们将会发现,

根据
这里将

因此,从频域上看,可得到如下结论:
4.1.2 小结
由O.N.BO.N.B为:
根据一开始的定义:
- 当
闭包:
是拓扑空间, ,则包含 的所有闭集的交称为 的闭包,记为 。 由定义得
是包含 的最小闭集,因为由闭集的任意交是闭集得 是闭集
- 当
,当 时, , 时,同样有 。 因为若
综上:
可得:
是
4.2 正交多分辨分析
设
-
单调性/嵌套性:
-
稠密性:
-
唯一性:
-
伸缩性:
-
构造性:
O.N.B
则称
由以上MRA定义,可得如下几条结论:
-
O.N.B: -
-
-
-
这一条的证明参考第19讲 06:00分钟。
-
-
若
O.N.B,则
O.N.B,由
上式称为:尺度方程,其中
尺度方程的频域形式为:
其中,记
上式称为:小波方程。其中
小波方程的频域形式为:
定义带通滤波器:
此时,小波方程的频域形式为:
(视频20讲 05:00分钟)
|
重要引理:
设 大白话就是:信号 |
上述引理的简要证明:
若在时间域上的整数平移构成 O.N.S,即意味着:。
按照内积的定义:其中进行了变量代换:
。详细解释(视频20讲 15:00分钟)。
根据此引理,可知由于O.N.S,故:
上式说明,如果尺度函数O.N.S,那么它对应的低通滤波器满足上式形式,这是一个很有名的滤波器——共轭滤波器。
- 进一步推广,有:
把上述三个条件合写成矩阵的形式,首先引入一个记号
此时有:
O.N.S,O.N.S,
若
构造的
的脉冲响应系数。
(21讲 10:00分钟)验证O.N.B:
显然,O.N.S ,O.N.S。下面要证明O.N.B。
记
- 对于
因为
两边进行傅里叶变换,有:
其中,
证明
由于
再由
将上述两式写为矩阵形式:
所以可得:
到此,便证明了O.N.B。
|
回顾总结:
1️⃣ 2️⃣ 3️⃣ |
4.3 正交小波构造(特例)
取带通滤波器
显然有:
另外:
此时:
故
(23讲)
(一) Haar小波的MRA
综上,
根据尺度方程可得:
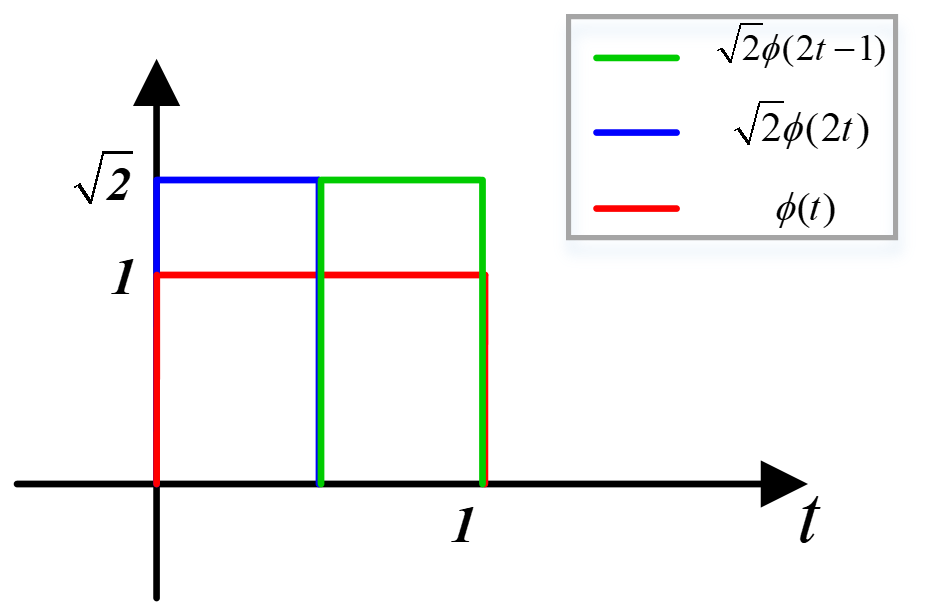
可得:
其对应的频域为:
则有:
由此,可构造正交小波:
此外,另一种算法为:直接计算出系数
由
所以,通过对比等式两端,可得(前提是上述等式两边都是周期为
(24讲 18:00)
带入计算可得:
所以有:

5 小波算法
5.1 多分辨分析回顾
按上述讲解的逻辑体系,多分辨分析可分为两个部分:一是闭的线性子空间序列
分析的信号所在的空间为
尺度方程和小波方程体现的是不同线性子空间之间的正交分割关系:
尺度方程:
其系数可通过内积投影计算:
其系数是
所以有:
即
5.2 小波方程
其中,系数:
当
同理可得:
综上,可得:O.N.B。
5.3 子空间关系
(25讲结束)
参考链接:

 小波变换基础
小波变换基础


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现