合成孔径雷达成像算法与实现

2 信号处理基础

2.1 线性卷积

(一) 离散时间卷积

一维离散时间卷积可写为：

$$\begin{array}{rl}y(n)& =s(n)\otimes h(n)\\ & =\sum _{m=0}^{M-1}s(n-m)h(m)\\ & =\sum _{m=n-(M-1)}^{n}s(m)h(n-m)\end{array}$$

其中，滤波器的长度为$M$个采样，其在积分域$[0,M-1]$之外被赋为0。假设滤波器长度$M$短于信号长度$K$(SAR数据即属于这种情况)。上式中的下标表明波器是因果的，时刻$n$的输出只与$n$和$n$之前的信号有关。

利用上式，下图示意了$K=8$点信号与$M=3$点滤波器之间的线性卷积。这也是MATLAB中函数conv(s，h)的计算原理。信号为正常时序，滤波器则为反褶时序。图中给出了两个循环位移位置上的滤波器，一个是在信号开始位置$n=0$，一个是在信号结束位置$n=9$在这两个位置之间，滤波器以每次移过一位的规律向右滑动，在每个位置上进行内积计算，即可得到一个输出样本。

滤波后的输出在$n=0,1,2,\cdots ,9$之间非零。但要注意到在$n=0,1,8,9$上，信号仅与滤波器系数的子集相乘，故输出结果是部分卷积的，在图中以小菱形表示。前两个点对应于滤波器初始条件未确定时的输出。其余(图中大菱形)为信号与滤波器系数的全集相乘输出结果，是完全卷积的。

部分卷积点在某些应用中很有用，但在其他情况下却并不需要。称在$n=2,\cdots ,7$时刻得到的$K-M+1=6$个输出点称为有效输出点(goodoutput point)，而其他输出点则被丢弃。MATLAB中的conv(s，h)函数则是对上图中所有$K+M-1=10$个输出点进行计算。使用DFT计算卷积时同样存在边缘效应。这些多余的边缘点即为之后讨论的“弃置”区。

以下为一个$K=8,M=3$的一维线性卷积示例：

$$\left\{\begin{array}{c}1,3,-1,5,2,6,4,-2\end{array}\right\}\otimes \left\{\begin{array}{c}1,2,3\end{array}\right\}=\left\{\begin{array}{c}1,5,8,12,9,25,22,24,8,-6\end{array}\right\}$$

6个有效输出点是$\left\{\begin{array}{c}8,12,9,25,22,24\end{array}\right\}$。边缘点或部分卷积点是$\left\{\begin{array}{c}1,5\end{array}\right\}$和$\left\{\begin{array}{c}8,-6\end{array}\right\}$。

2.2 离散傅里叶变换DFT

(一) DFT的基本定义

对于长度为$N$的离散信号$g(n)$，DFT变换对可写为：

$$\begin{array}{l}\text{ DFT : }G(k)={\displaystyle \sum _{n=0}^{N-1}g(n)\exp \{-j{\displaystyle \frac{2\pi kn}{N}}\}k=0,\cdots ,N-1}\\ \text{ IDFT : }g(n)={\displaystyle {\displaystyle \frac{1}{N}}\sum _{k=0}^{N-1}G(k)\exp \{+j{\displaystyle \frac{2\pi kn}{N}}\}n=0,\cdots ,N-1}\end{array}$$

其中$G(k)$的$N$个值称为谱系数。注意，上式中的尺度因子${\displaystyle \frac{1}{N}}$在一些实际应用中可忽略但要正确地重建信号$g(n)$的幅值，必须使用这个因子。

时域第一个点$g(0)$对应的时刻为零时刻，信号在时域上以${\displaystyle \frac{1}{f_s}}$等间隔采样，$f_s$为采样频率。频域第一个点$G(0)$对应的频率为零频，频域采样间隔则为${\displaystyle \frac{f_s}{N}}$。因此，频谱样本$G(k)$对应的频率为${\displaystyle \frac{k{f}_s}{N}}$(即复正弦信号频率在$N$个样本点内经历了$k$个周期)。

由于复指数函数的周期为$2\pi$，以下DFT性质对于任何整数$M$都成立:

$$\begin{array}{l}g(n+MN)=g(n)\\ G(k+MN)=G(k)\end{array}$$

注意，上式中第1个子式表明时间序列在分析区间$n=0,1,\cdots ,N-1$外具有周期性。实际上序列通常是非周期的，但在进行DFT时必须使用周期假定。后面讨论的泄漏就来自于非周期信号的周期假设。上式中第2个子式表明离散时间序列的频谱也是周期的。与时序列的周期性或有限长度不同，频谱的周期性源自采样定理。由于频谱是周期的，在DFT的某一输出点$k$，观察到的能量可能来自连续时间信号的任一${\displaystyle \frac{k{f}_s}{N}}\pm M{f}_s$频率分量。这种$M$值的不确定性称为谱模糊。在一些SAR操作中，$M$是非常重要的。

(二) FT/DFT的基本性质和注意点

• 复共轭：信号的傅里叶变换取复共轭，并将频率轴反褶，与信号复共的傅里叶变换相等：

$$g^{\ast }(t)⟷G^{\ast }(-f)$$

• 尺度变换：某一域中的尺度变换相当于另一域中的“压缩”或“拉伸”，对非零尺度因子$a$：

$$g(at)⟷\frac{1}{|a|}G(\frac{f}{a})$$

结合时域内插零来考虑。

• 位移/调制：该性质对滤波器设计和插值等应用非常重要。信号在时域中右移$t_0$，等效于在频域与一个负指数线性相位函数相乘。频谱右移相当于在时域用一个正指数函数对信号进行调制。对于连续时间，有：

$$\begin{array}{l}g(t-t_0)⟷G(f)\exp \left\{\begin{array}{c}-j2\pi f{t}_0\end{array}\right\}\\ g(t)\exp \left\{\begin{array}{c}j2\pi f_{0}t\end{array}\right\}⟷G(f-f_0)\end{array}$$

对于离散时间，所有位移都具有周期性，等效于位移值对$N$取模。

• 对称性：如果$g(t)$是实信号，则频谱$G(f)$满足共轭对称性，即$G(f)$的实部关于零频对称而虚部关于零频反对称：

$$G(f)=G^{\ast }(-f)$$

复信号则不具有这种对称性。即复信号中的正负频率是可区分的，因而在复信号中正负频率可以单独表示信息。

• 补零：在离散时间下，某一域(频域或时域)中的序列补零相当于对另一域进行升采样。这使得另一域中的数据量增大，但不会改变序列的信息内容(例如带宽)。补零可以用于对序列进行插值，按某一特定值调整样本间隔或使变换长度便于高效处理。

2.3 卷积的离散傅里叶变换计算(参考链接2.1)

DFT和IDFT中默认前提是周期假设和循环寻址(循环卷积)，卷积实际上是周期卷积或循环卷积。通过将序列补零至合适的长度，就可以利用DFT进行线性卷积。下说明了DFT的循环性质。在图中，较长的信号序列围绕圆周按顺时针方向排列。为满足周期性假设，序列结束点$s_7$，与序列开始点$s_0$相连。第二个序列，即滤波序列，绕圆周逆时针排列，并通过补零使圆周闭合。每次将滤波器沿顺时针方向移动一位(旋转内圆)，对应点相乘后再相加(点乘)即可完成循环卷积。重复$N$次得到$N$个值，其中$N$是较长序列的长度。

这种方式实现的循环卷积有一个不同于线性卷积的有趣性质。如果内圆位置如图所示，或者再顺时针旋转一位，滤波器样本同时跨越了信号序列的开始点和结束点。如果信号序列具有周期性，则结果是正确的，但信号很可能是非周期的，那么在这两个点上得到的输出则是错误的。这些源自循环卷积卷绕错误的点应从输出序列中去除，将其称为弃置点。在前述$8$个点的例子中，$2$个点是弃置点，$6$个点是有效点。

例如，当使用DFT时，上面$K=8,M=3$的一维线性卷积的卷积结果变为：

$$\left\{\begin{array}{c}1,3,-1,5,2,6,4,-2\end{array}\right\}\otimes \left\{\begin{array}{c}1,2,3\end{array}\right\}=\left\{\begin{array}{c}9,-1,8,12,9,25,22,24\end{array}\right\}$$

其中$3$点滤波器补零至$8$点。$6$个有效点与前面相同，但将前面一维线性卷积式的边缘点叠加，就会发现：$(1,5)+(8,-6)=(9,-1)$，这两个点正是循环卷积中的卷绕点。

即：弃置点的个数为$M-1$($M$为滤波器长度)。

🐹 补零详解：

为了避免错误输出，将两个序列长度都延拓补零至$N=n_1+n_2-1$，其中$n_1$和$n_2$为序列初始长度。图2.4(b)对此进行了示意。为了提高效率，DFT长度$N$通常选为$2$的幂。例如，假设$n_1$和$n_2$,的长度分别为$3100$和$900$，则适宜的FFT长度应为$4096$，每个信号都应补零至这个长度。最终结果包括$4096$个样点，其中$n_1-n_2+1=2201$个点是完全卷积结果，$2(n_2-1)=1798$个点是部分卷积结果，其余$N-n_1-n_2+1=97$个点为多余的零点。

部分卷积结果通常是不需要的(弃置区？？？)。令$n_1$为较长序列的长度。如果使用DFT，则最小DFT长度为$n_1$，只有较短的序列$n_2$需要补零至DFT长度。如果使用FFT，则$n_1$和$n_2$序列都要补零至适宜的长度。无论是DFT还是FFT，通过循环卷积都能得到$n_1-n_2+1$个完全卷积的正确结果，如图2.4(a)所示。

在MATLAB中，循环卷积通过以下函数实现：

$$\text{iffft}(\text{fft}(s,N).\ast \text{fft}(h,N))$$

可以根据需要的补零量或/和FFT的计算效率来选择FFT的长度$N$。在MATLAB中，补零是在每个序列结尾处的内置补零。

2.4 信号采样

当对采样信号进行$N$点DFT时，输出序列第一个样本的频率为零，最后一个样本的频率为${\displaystyle \frac{(N-1)f_s}{N}}\approx f_s$。为了便于分析和说明，通常将DFT输出序列的左右两半互相交换。这种操作在MATLAB中是通过fftshift完成的。互换后，序列第一个样本频率为$-{\displaystyle \frac{f_s}{2}}$，最后一个样本频率为${\displaystyle \frac{(N-2)f_s}{2N}}$。对于实信号，DFT输出序列的前一半就可以完整地描述信号，后一半则是冗余的。

(一) 实信号与复信号

现实世界中的所有信号都是实信号。但在数字信号处理器中，对复信号进行操作则更方便和高效。例如，DFT所处理的序列就是复序列。在实际情况下，可以通过复解调过程(又称正交解调)，将实信号转换为含有相同信息的复信号。在该运算中，信号与具有一定频率的余弦波混合(相乘)，滤除高频分量后的输出称为实通道信号。与此同时，信号与同一频率的正弦波混合，其输出称为虚通道信号。这两路信号经同步采样器采样后得到一个复采样。以上操作是可交换的，即先对实信号进行采样，然后在离散域完成解调。复信号转换也可通过希尔伯特变换实现、此时信号将产生${\displaystyle \frac{\pi }{2}}$的相移。

下图表明实信号的频谱关于零频是共对称的，而复信号则不满足频谱对称条件。

• 信号带宽

信号带宽对采样要求是非常重要的。对于实信号仅考虑正频率即可。如果信号的最高频率为$f_2$，最低(正)频率为$f_1$，则信号带宽为$\mathrm{\Delta }f=f_2-f_1$。

对于复信号其正、负频率都要考虑。此时，包含负频率之后的最低信号频率为$f_1$。信号带宽的计算仍为$\mathrm{\Delta }f=f_2-f_1$。在上图2.6中，水平实线所涵盖的范围即为带宽。所有四种情况下的带宽约为$75Hz$。当所有能量几乎都集中于通带内时，带宽似乎很好定义。但实际情况并非总是如此，而且从理论上讲,有限长度信号不可能是带限的。为避开这一问题，可以在忽略低于一定基准能量的前提下将有限长度信号等效为带限信号。因此，只有高于“主要”基准的能量是需要考虑的。该基准通常定在峰值能量以下$3\text{dB}$处(在某些应用中也使用$10\text{dB}$基准)。实际上模信号一般含一些多余的高频分量(如白噪声)。为尽可能降低采样率，可以在采样前使用抗混叠滤波器将信号带宽限制在感兴趣的频谱范围内。

• 基本频率范围（重点）

一定采样率下的基本范围是指能完整保存信号信息的最低频率集合。如果采样率为实信号的基本频率范围为$0\sim {\displaystyle \frac{f_s}{2}}$，复信号的基本频率范围为$-{\displaystyle \frac{f_s}{2}}\sim {\displaystyle \frac{f_s}{2}}$或$0\sim f_s$。图2.6通过水平点线对基本范围进行了示意，其中假设实信号采样率为$200\text{Hz}$，复信号采样率为$100\text{Hz}$

(二) 奈奎斯特采样频率和混叠

由于每个复信号样本的信息量是实信号样本的两倍，故两者的采样要求是不同的。

• 实信号采样

奈奎斯特采样定理表明，对于有限带宽的连续基带实信号，为使采样能正确描述信号信息，采样率必须高于最高信号频率的两倍，该最小采样率称为奈奎斯特采样率。实信号采样定理的另一种表述是，信号所包含的每一正弦波在一个周期内至少被采样两次。

为说明采样要求，考察图2.7实线所示的$300\text{Hz}$连续正弦波。图中示意了$3$个周期，持续时间为$10\text{ms}$。首先，令信号的采样率$f_s=800\text{Hz}$，如图中星号所示。该采样率相当于每周期$2.667$个采样点，高于奈奎斯特采样率。通过给定的采样点可得无限多个正弦波。由于连续正弦波的频率在$0$和${\displaystyle \frac{f_s}{2}}$之间(即在基本范围内)，故只有唯一一个正弦波，即图中实线所示的正弦波。在这种情况下，初始信号频率($300\text{Hz}$)处于基本频带内，通过采样重建的信号频率是正确的。

现在，用$400\text{Hz}$频率(每周期$1.333$个采样点)对同一连续信号采样，如图2.7中菱形所示。从图中虚线可见，由采样点得到的最低频率正弦波在频率上是错误的。即经采样重建后的信号与初始信号不同。这种由初始信号频率的错误采样所导致的观测频率改变称为混叠。当以$400\text{Hz}$采样时由后面的混叠方程表示的可观测频率仅有$400-300=100\text{Hz}$(通过简单绘制频谱图，然后左右平移基带频率$f_s$可知$0\sim 100\text{Hz}$没有混叠，$100\sim 300\text{Hz}$发生混叠)。

• 复信号采样

复信号的奈奎斯特采样率与信号带宽相等。考虑到复样本(一对实部/虚部)携带的信息是实样本的两倍，其与实信号情况并不矛盾。图2.9示意了采样对复信号频谱的影响。其中，初始信号带宽为$300\text{Hz}$，采样率$f_s=400\text{Hz}$，图中每一行的中心频率以每次$100\text{Hz}$从$0\text{Hz}$递增至$400\text{Hz}$。

图2.9说明了复信号的如下2个独有性质：
   ① 首先，复信号的频谱关于零频是不对称的。
   ② 其次，基本频率范围为$[-{\displaystyle \frac{f_s}{2}},{\displaystyle \frac{f_s}{2}}]$(见图中最左侧的一对虚线)。虚线是混叠边界，其为实信号的两倍。

图2.9第1行中的连续复信号带宽处于采样信号的基本频率围内不会出现混叠(如右列所示)。随着中心频率的增加，信号带宽移出基本频率范围，某些能量进人由最右侧虚线对标识的混叠区。此时，混叠区中的每一信号分量会被采样平移至基本频率区域的相关位置。

可以看到复信号的混叠模式比实信号简单，即频率轴方向保持不变。因此，混叠信号的不同分量之间不会相互影响，只要采样率高于奈奎斯特采样率采样频谱就可以保存连续信号的全部信息。当对采样信号进行DSP操作时，在采样前后都可以很方便地进行频谱搬移，以使采样信号具有连续频谱(见图中第1行到第5行)。

• 混叠方程

由采样导致的频率变化可以通过采样方程来表示。复信号采样后的可观测频率为：

$$F_{\text{apparent\_complex }}=F_{\text{continuous }}-\left\{\text{ round }\left(F_{\text{continuous }}/f_s\right)\right\}{f}_s$$

其中$F_{\text{continuous }}$是连续信号频率，$f_s$是采样率，$\text{round}$表示取整。注意，复信号的$F_{\text{continuous }}$可以是负的。

由于实信号中的折叠不是单向的，所以混叠后的可观测频率比复信号复杂一些。其与复信号可观测频率的关系为：

$$F_{\text{apparent\_real }}=|F_{\text{apparent\_complex }}|$$

图2.10示意了混叠频率与实际连续信号频率的关系。由上两式可以发现实信号和复信号的混叠模式不同。注意，实信号中的混叠为扇状折叠模式。之后会进一步讨论由欠采样导致的混叠。

通过图2.5的频谱复制可以给出采样定理和混的另一种解释。首先，如果图下半部分的各频谱区不相交，则符合采样定理。此时，频谱不存在混叠和失真，可以重建连续信号。其次，如果连续信号频率在$\pm {\displaystyle \frac{f_s}{2}}$之间，则采样信号是无混叠的，否则将会出现混叠。如果采样前信号的频率超出$\pm {\displaystyle \frac{f_s}{2}}$(即图2.8和图2.9中的混叠区)那么采样后可观测频率范围小于$\pm {\displaystyle \frac{f_s}{2}}$。

DFT只能“观察”到频谱的基本部分(即基带频谱)。换话说，DFT 只能得到图2.9右边一列所示的频谱。通过观察DFT输出不可能判断出初始信号所处的“实际频段”。有时，为了正确进行SAR处理，必须知道初始信号频率。第5章和第12章将对此进行讨论。

注意“正确采样”与“混叠”之间存在微妙的差异。
前者指信号能被正确重建，后者指采样造成的频率变化。
遵循奈奎斯特定理的采样是正确的，而当频率超出基本频率范围，则会出现混叠。不正确的采样会出现混叠，而混叠并不总意味着不正确的采样(见图2.8最后一行)。

2.5 平滑窗

锐化窗或平滑窗是一个从中心峰值点向两侧衰落的实函数，在信号处理中用来缓解有限长度信号的截断影响。由于加窗具有使孔径中心的权值高于两端权值的效应，故又称为“加权”。在脉冲压缩中使用窗来控制旁瓣，同时尽可能保持高的分辨率。由于旁瓣的降低会导致分辨率的展宽，故需进行折中考虑。通常在处理中使用Kaiser窗，因为该窗函数有一个用来调整加权度进而均衡旁瓣/分辨率的参数。

(一) 频谱泄露的概念

提到加窗，首先要了解一下频谱泄露的概念。

一些人可能会说，频谱泄露就是频谱中除了本来该有的主瓣之外，还会出现本不该有的旁瓣；一下子主瓣、旁瓣这些概念都来了，这些一些很抽象的概念，搞得我们很难去理解。其实频谱泄露就一句话：原来信号的频谱中出现了本不该有的频率分量！

(二) 频谱泄露的原因

原来的信号的序列我们认为是无限长的，但我们要分析某个信号的频谱的时候只能对它有限长度的序列进行分析，这么一来，就相当于时域上对它进行了加窗，但这并不能代表我们的信号啊，于是就导致了频谱泄露。

归根结底，频谱泄露的原因就是加窗导致的序列长度有限。

不同的窗函数对信号频谱的影响是不一样的，这主要是因为不同的窗函数产生泄漏的大小不样，频率分辨能力也不一样。为了不影响截短序列的相位响应，通常需要窗函数保持线性相位。

(三) 加窗的原因

问：既然频谱泄露是不好的，那我们就想要消除它。但问题是频谱泄露能够消除吗？

答：理论上是不能。因为时域样点的长度L(即窗长度)始终是有限的，如果我们进行DFT采样，那么始终就会采到“主瓣”“旁瓣”，所以频谱泄露是不能消除的。

选择选择合适的窗函数，加窗是消除频谱泄露的原因之一。

在时域上看，加窗其实就是将窗函数作为调制波，输入信号作为载波进行振幅调制。矩形窗对截取的时间窗内的波形未做任何改变，即只是截断信号原样输出。

更普遍地，绝大部分窗函数形状都具有类似从中间到两边逐渐下降的形状，只是下降的速度等细节上有所区别。降低截断引起的泄漏，所有窗函数都是通过降低起始和结束处的信号幅度来减小截断边沿处信号突变产生的额外频谱。

不同的窗函数，产生泄漏的大小不一样，频率分辨能力也不一样。信号的截断产生了能量泄漏，而用FFT算法计算频谱又产生了栅栏效应，从原理上进这两种误差都是不能消除的，但是我们可以通过选择不同的窗函数对它们的影响进行抑制。

或者也可以理解为“如何解决脉冲压缩引起的旁瓣问题？”

将线性调频信号通过匹配滤波器处理后，输出的信号是具有辛克(sinc)函数特征的窄脉冲，包含主瓣和多个距离旁瓣。若旁瓣较高，会导致处理时认为其为主瓣，造成虚假目标误判，同时也容易淹没附近的弱小目标，造成目标漏判。因此，对于脉冲压缩技术，需要研究旁瓣抑制方法，提高主副瓣比。

常用的旁瓣抑制方法就是进行加权处理即加窗处理。但加权在降低旁瓣的同时，也付出了信噪比降低和主瓣展宽等代价。如下图所示，是线性调频信号直接进行匹配滤波的仿真结果和加窗处理后的仿真结果。

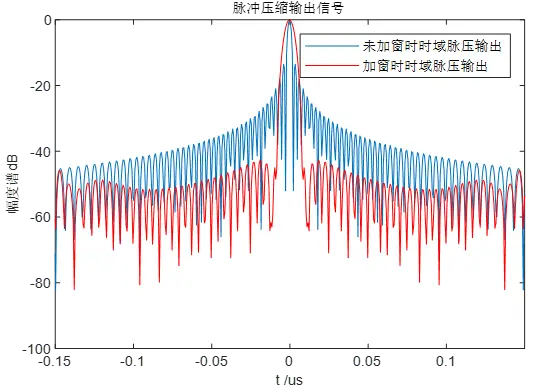
由上图可见，加窗后的脉冲压缩输出信号旁瓣电平明显降低，有效实现了旁瓣抑制目标，但同时造成主瓣展宽和信噪比降低，牺牲了一定程度上的距离分辨率。

(四) 时域加窗和频域加窗

• 时域加窗

通常时域上加窗更普遍，时域截断带来了频谱泄漏，窗函数是为了减小这个截断效应，被设计成一组加权系数$w(n)$。

时域域加窗在时域上表现的是点乘，因此在频域上则表现为卷积。卷积可以被看成是一个平滑的过程，相当于一组具有特定函数形状的滤波器，因此，原始信号中在某一频率点上的能量会结合滤波器的形状表现出来，从而减小泄漏。

• 频域加窗

频域加窗在频域上表现为点乘，这是为了减小脉冲压缩后时域的距离向旁瓣，而对匹配滤波器的频率响应加窗。我们知道线性调频脉冲的频率响应近似为矩形，对其乘以窗函数可得到修正后的频率响应。

(五) 常见窗及其性质

• 矩形窗：优点是主瓣比较集中；缺点是旁瓣较高，并有负旁瓣，导致加窗过程中带进了高频干扰和频谱泄漏。

• 汉宁窗：又称升余弦窗，汉宁窗使主瓣加宽并降低，旁瓣则显著减小，从减小泄漏观点出发，汉宁窗优于矩形窗。但汉宁窗使主瓣加宽，相当于分析带宽加宽，频率分辨力下降。汉宁窗函数的最大旁瓣值衰减$-31\text{dB}$，但是主瓣宽度比矩形窗函数的主瓣宽度增加了1倍。

• 汉明窗：也是余弦窗的一种，又称改进的升余弦窗，与汉宁窗的加权系数不同。汉明窗加权的系数能使旁瓣达到更小。汉明窗的第一旁瓣衰减为$-42\text{dB}$，其旁瓣衰减速度比汉宁窗衰减速度慢。汉明窗与汉宁窗都是很有用的窗函数。

(六) 栅栏效应简要介绍

首先来看栅栏效应，由于DFT是在DTFT的基础上对频域进行采样，因此频域就会变成离散的点，就好像通过栅栏观察频谱一样，因此叫做栅栏效应。

在对信号进行采样后，得到是采样点上的对应的函数值。其效果如同透过栅栏的缝隙观看外景一样，只有落在缝隙间的少数景象被看到，其余景象均被栅栏挡住而视为零，这种现象称为栅栏效应。

不管是时域采样还是频域采样，都有相应的栅栏效应。只是当时域采样满足采样定理时，栅栏效应不会有什么影响。而频域采样的栅栏效应则影响很大，“挡住”或丢失的频率成分有可能是重要的或具有特征的成分，使信号处理失去意义。

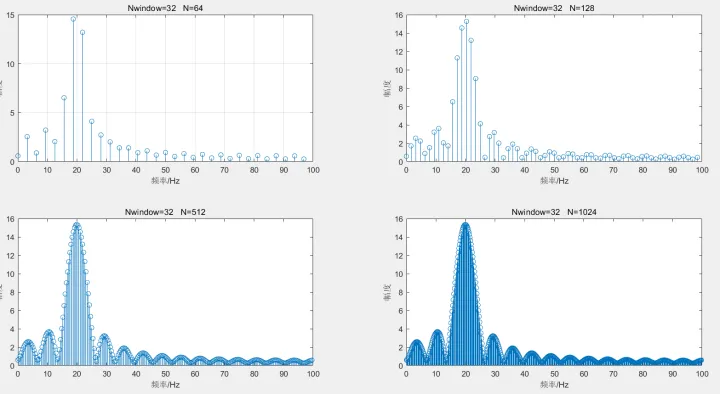
栅栏效应可以通过时域补零来减小(相当于频域插值)，同时也相当于增大频域的采样点数（因为频域采样点数等于时域信号的点数）。下图是表示时域信号有效长度不变的情况下，分别补零不同的点数对应的结果，可以看出补零越多，栅栏效应越小。

参考链接2.1：1.3. DFT的特性 - CSDN
参考链接2.2：频率域采样的理解 - beike-lucky的文章 - CSDN
参考链接2.3：雷达信号“加窗”的目的和效果 - 360个人图书馆
参考链接2.4：深入浅出的理解频谱泄露 - 自语的骆驼 - CSDN
参考链接2.5：加窗原理和频谱泄露 深入理解 - 马尚先生的文章 - 知乎

X 驻定相位原理(POSP)

X.1 POSP的核心思想(定性分析)

POSP用于估计傅里叶变换的条件：信号相位变化非常快，以至于在做积分时，只有在驻相点附近的积分才不为零。

在数字信号处理中，经常需要将一个时域信号转换到频域进行处理，比如说需要对其进行傅里叶变换，那么对于这样的一个复数信号：

$$u(t)=a(t){\mathrm{e}}^{\mathrm{j}\phi (t)}$$

对其进行傅里叶变换时，就会得到如下式子：

$$S(\omega )={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}a(t){\mathrm{e}}^{\mathrm{j}\phi (t)}{\mathrm{e}}^{-\mathrm{j}\omega t}\mathrm{d}t$$

这个积分事实上是很难计算的，并且通常没有解析解。我们现在通常是对时域信号以高于奈奎斯特频率的频率对其进行采样，再进行FFT，利用计算机求得数值解，但在没有计算机的年代，人们只能通过其他方法在特定前提下对其进行估算，比如驻定相位近似(Stationary Phase Approximation)。

观察如下积分式：

$$P=\int U(t)\cos (V(t))\mathrm{d}t=\mathrm{Re}[\int U(t){\mathrm{e}}^{\mathrm{j}V(t)}\mathrm{d}t]$$

其中，$U(t)$是幅度包络，$V(t)$是相位。给定前提相位$V(t)$对于时间来说是捷变的，幅度$U(t)$是缓变的。

🐋 驻定相位核心思想：

也就是说，当相位随时间变化很快的时候，那么在相位变化一个周期的时间内，幅度可视为一个常数，对其积分，由于$\cos V(t)$的正部分和负部分的面积相互抵消，上式的积分接近于零就近似为零，于是上述积分的值就基本上由$V(t)$变化缓慢的点决定，即${\displaystyle \frac{\mathrm{d}V(t)}{\mathrm{d}t}}=0$(相位梯度为零的点, Critical Points)附近，由于相位变化率很小，相位有很长时间的滞留，才能使上式的积分显著不为零。

X.2 POSP计算窄带信号频谱(定量分析)

以窄带信号(高频扰动信号)：$x(t)=A(t)\exp (\mathrm{j}\theta (t))$的傅里叶变换为例，应用POSP计算$x(t)$的FT。

根据傅里叶变换的定义，可得：

$$\begin{array}{rl}X(\omega )& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}A(t){\mathrm{e}}^{\mathrm{j}\theta (t)}{\mathrm{e}}^{-\mathrm{j}\omega t}\text{ d}t\\ & ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}A(t){\mathrm{e}}^{-\mathrm{j}[\omega t-\theta (t)]}\text{ d}t\\ & ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}A(t){\mathrm{e}}^{-\mathrm{j}\varphi (t,\omega )}\text{ d}t\end{array}$$

式中，$A(t)$是包络信息，$\varphi (t,\omega )$是相位信息。积分时正部分和负部分面积相抵消，上式积分接近零。只有在${\displaystyle \frac{\mathrm{d}(\omega t-\theta (t))}{\mathrm{d}t}}=0$点附近，由于相位变化率很小，相位值有很长时间的滞留，才能使上式积分显著不为零。

设$t_k$是驻定相位点，即：

$${{\displaystyle \frac{\mathrm{d}(\omega t-\theta (t))}{\mathrm{d}t}}|}_{t=t_k}=0⟹\omega ={\theta }^{\prime }(t_k)$$

对于相位项$\omega t-\theta (t)$在驻定相位点$t_k$附近进行泰勒展开：

$$\omega t-\theta (t)=[\omega t_k-\theta (t_k)]+[(\omega -{\theta }^{\prime }(t_k))(t-t_k)]+[-\frac{{\theta }^{″}(t_k)}{2}(t-t_k{)}^2]+\cdots$$

忽略高次项，且由于$\omega ={\theta }^{\prime }(t_k)$，可将上式化简为：

$$\omega t-\theta (t)=\omega t_k-\theta (t_k)-\frac{{\theta }^{″}(t_k)}{2}(t-t_k{)}^2$$

带入$X(\omega )$表达式中：

$$X(\omega )=A(t_k)\exp (-\mathrm{j}(\omega t_k-\theta t_k)){\int }_{t_k-\delta }^{t_k+\delta }\exp (j\frac{{\theta }^{″}(t_k)}{2}(t-t_k{)}^2))\text{ d}t$$

做如下变量代换：

$$\{\begin{array}{l}u=t-t_k\\ {\displaystyle \frac{{\theta }^{″}(t_k)}{2}}{u}^2={\displaystyle \frac{\pi y^2}{2}}\end{array}⟹\mathrm{d}t=\mathrm{d}u=\sqrt{\frac{\pi }{{\theta }^{″}(t_k)}}\text{ d}y$$

带回$X(\omega )$的表达式，有：

$$X(\omega )=2A(t_k)\sqrt{\frac{\pi }{{\theta }^{″}(t_k)}}\exp \left[-\mathrm{j}\left(\omega t_k-\theta (t_k)\right)\right]{\int }_0^{\sqrt{\frac{{\theta }^{″}(t_k)}{\pi }}\cdot \delta }\exp \left(\mathrm{j}\frac{\pi y^2}{2}\right)\mathrm{d}y$$

其中，上式中的积分为菲尔涅积分。若积分上限较大，则非尔涅积分趋于定值：${\displaystyle \frac{1}{\sqrt{2}}}\exp \left(\mathrm{j}{\displaystyle \frac{\pi }{4}}\right)$。

因此，信号的傅里叶变换为：

$$\begin{array}{}\text{(**)}& X(\omega )=A(t_k)\sqrt{\frac{2\pi }{|{\theta }^{″}(t_k)|}}\exp [-\mathrm{j}(\omega t_k-\theta (t_k)-\frac{\pi }{4})]\end{array}$$

X.3 POSP计算线性调频信号的频谱

设LFM信号为：

$$u(t)=\mathrm{rect}\left(\frac{t}{T_p}\right)\exp (\mathrm{j}\pi k_r{t}^2)$$

根据定义，其傅里叶变换为：

$$\begin{array}{rl}U(\omega )& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}u(t){\mathrm{e}}^{-\mathrm{j}\omega t}\text{ d}t\\ & ={\int }_{-T_p/2}^{+T_p/2}{\mathrm{e}}^{\mathrm{j}(\pi k_r{t}^2-\omega t)}\text{ d}t\\ & =\exp (-\mathrm{j}\frac{{\omega }^2}{4\pi k_r}){\int }_{-T_p/2}^{+T_p/2}\exp \left[\mathrm{j}{(\sqrt{\pi k_r}\cdot t-\frac{\omega }{2\sqrt{\pi k_r}})}^2\right]\text{ d}t\end{array}$$

做变量代换：

$${(\sqrt{\pi k_r}\cdot t-\frac{\omega }{2\sqrt{\pi k_r}})}^2=\frac{\pi }{2}{x}^2⟹x=\sqrt{2\pi k_r}\cdot t-\frac{\omega }{\pi \sqrt{2k_r}}⟹\mathrm{d}x=\sqrt{2k_r}\mathrm{d}t$$

则有

$$U(\omega )=\frac{1}{\sqrt{2k_r}}\exp \left(\mathrm{j}\frac{{\omega }^2}{4\pi k_r}\right){\int }_{-X1}^{X2}\exp \left(\mathrm{j}\frac{\pi x^2}{2}\right)\text{ d}x$$

其中：

$$\begin{array}{rl}& X_1=\sqrt{2k_r}\frac{T_p}{2}+\frac{\omega }{\pi \sqrt{2k_r}}=\frac{\pi k_r{T}_p+\omega }{\pi \sqrt{2k_r}}\\ & X_2=\sqrt{2k_r}\frac{T_p}{2}-\frac{\omega }{\pi \sqrt{2k_r}}=\frac{\pi k_r{T}_p-\omega }{\pi \sqrt{2k_r}}\end{array}$$

注：菲涅尔积分

$$\begin{array}{cc}& C(x)={\displaystyle {\int }_0^X\cos (\frac{\pi x^2}{2})\text{ d}x}\\ & S(x)={\displaystyle {\int }_0^X\sin (\frac{\pi x^2}{2})\text{ d}x}\\ & C(-X)=-C(X)\\ & S(-X)=-S(X)\\ & \underset{X\to \mathrm{\infty }}{lim}C(X)=\underset{X\to \mathrm{\infty }}{lim}S(X)=0.5\end{array}$$

则矩形包络LFM信号的频谱精确解为：

$$U(\omega )=\frac{1}{\sqrt{2k_r}}\exp (-\mathrm{j}\frac{{\omega }^2}{4\pi k_r})[C\left(X_1\right)+jS\left(X_1\right)+C\left(X_2\right)+jS\left(X_2\right)]$$

其幅度谱和相位谱分别为：

$$\begin{array}{ll}& |U(\omega )|={\displaystyle \frac{1}{\sqrt{2k_r}}}\sqrt{[C(X_1)+C(X_2){]}^2+[S(X_1)+S(X_2){]}^2}\\ & \phi (\omega )=-{\displaystyle \frac{{\omega }^2}{4\pi k_r}}+\arctan {\displaystyle \frac{S(X_1)+S(X_2)}{C(X_1)+C(X_2)}}\end{array}$$

在感兴趣的频率范围内，分式：

$${\displaystyle \frac{S(X_1)+S(X_2)}{C(X_1)+C(X_2)}}\approx 1$$

当时宽带宽积足够大时，有：

$$\begin{array}{ll}& |U(\omega )|\approx {\displaystyle \frac{1}{\sqrt{k_r}}}\\ & \phi (x)\approx {\displaystyle \frac{{\omega }^2}{4\pi k_r}}+{\displaystyle \frac{\pi }{4}}\end{array}$$

由于精确解难以计算，所以利用上述第二小节中窄带信号的频谱为式$(\ast \ast )$，那么对于矩形包络的LFM信号，

$$\begin{array}{rl}& A(t)=\mathrm{rect}\left(\frac{t}{T_p}\right)\\ & \theta (t)=\pi k_r{t}^2⟹{\theta }^{\prime }(t)=2\pi k_{r}t⟹{\theta }^{\prime \prime }(t)=2\pi k_r\\ & \frac{\mathrm{d}}{\mathrm{d}t}[\theta (t)-\omega t]=0⟹2\pi k_{r}t-\omega =0⟹t_k=\frac{\omega }{2\pi k_r}\end{array}$$

此时，利用驻定相位原理得到LFM信号的幅度和相位谱分别是：

幅度谱	相位谱
$\begin{array}{rl}|U(\omega )|& =\sqrt{2\pi }\frac{\mathrm{rect}\left({\displaystyle \frac{\omega }{2\pi k_r{T}_p}}\right)}{\sqrt{2\pi k_r}}\\ & =\frac{1}{\sqrt{k_r}}\mathrm{rect}\left(\frac{\omega }{\mathrm{\Delta }\omega }\right)\end{array}$	$\begin{array}{rl}\varphi (\omega )& =-\omega t_k+\theta \left(t_k\right)+\frac{\pi }{4}\\ & =-\omega \frac{\omega }{2\pi k_r}+\pi k_r{\left(\frac{\omega }{2\pi k_r}\right)}^2+\frac{\pi }{4}\\ & =-\frac{{\omega }^2}{4\pi k_r}+\frac{\pi }{4}\end{array}$

其中，$\mathrm{\Delta }\omega =2\pi (k_r\cdot T_p)=2\pi \times \mathrm{带}\mathrm{宽}$

x.4 快速POSP

设$g(t)$是一个调频信号：

$$g(t)=w(t)\exp (\text{j}\theta (t))$$

其中$w(t)$是实包络，$\theta (t)$为信号调制相位。假设与相位相比，包络为时间缓变函数。

该信号的频谱为：

$$\begin{array}{rl}G(f)& ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}g(t){\mathrm{e}}^{-\mathrm{j}2\pi ft}\text{ d}t\\ & ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}w(t){\mathrm{e}}^{-\mathrm{j}[2\pi ft-\theta (t)]}\text{ d}t\\ & ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}w(t){\mathrm{e}}^{-\mathrm{j}\varphi (t)}\text{ d}t\end{array}$$

最终，$G(f)$的频谱形式如下：

$$G(f)\approx C_{1}W(f)\exp \left[\mathrm{j}(\mathrm{\Phi }(f)\pm {\displaystyle \frac{\pi }{4}})\right]$$

其中变量定义如下：

• $C_1$为一个通常可忽略的常数

$$C_1=\sqrt{{\displaystyle \frac{2\pi }{|{\varphi }^{″}(t)|}}}$$

• $W(f)$为频域包络

$$W(f)=w[t(f)]$$

• $\mathrm{\Phi }(f)$为频域相位

$$\mathrm{\Phi }(f)=\varphi [t(f)]$$

• $t(f)$由信号时频关系给出

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\varphi (t)=0$$

注：${\displaystyle \frac{\pi }{4}}$的符号由$\varphi {}^{″}(t)$的符号给出。与$C_1$类似，在绝大多数分析中都可忽略该常数相位的影响。

参考链接X.1：驻定相位原理，以及在LMF信号中的实现（上） - world的文章 - 知乎
参考链接X.2：驻定相位原理（POSP）以及线性调频信号的频谱 - 寂静的以 - CSDN
参考链接X.3：(二)何为驻相定理？？？ - Marshall Over的文章 - 知乎

Y 信号升/降采样、时域插零/补零、频域插零/补零

首先直接抛下几个结论：

   ① 时域后补0，频域取样更密，也即频域内插；

   ② 时域内插0，则频域复制，且频谱被压缩；

   ③ 频域内插0，则时域产生镜像；

   ④ 频域后补0，会让时域数据内插。

Y.1 时域后补0

设离散信号$x(n)$的长度为$N$，在其后补$M$个$0$产生的新序列记为$y(n)$，在其前面补充$M$个$0$产生的新序列记为$z(n)$。

$x(n)$的DTFT为：

$$X_1(e^{\mathrm{j}\omega })=X_1(\omega )=\sum _{n=0}^{N-1}x(n)e^{-\mathrm{j}\omega n}$$

$x(n)$的DFT为：

$$X_2(k)=\sum _{n=0}^{N-1}x(n)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N}}nk)=X_1(\omega ){\mid }_{\omega =2\pi \frac{k}{N}}$$

$y(n)$的DTFT为：

$$Y_1(\omega )=\sum _{n=0}^{N+M-1}y(n)e^{-\mathrm{j}\omega n}=\sum _{n=0}^{N-1}x(n)e^{-\mathrm{j}\omega n}=X_1(\omega )$$

$y(n)$的DFT为：

$$\begin{array}{rl}{Y}_2(k)& =\sum _{n=0}^{N+M-1}y(n)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}nk)\\ & =\sum _{n=0}^{N-1}x(n)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}nk)\\ & =X_1(\omega ){\mid }_{\omega =2\pi \frac{k}{N+M}}\end{array}$$

$z(n)$的DTFT为：

$$\begin{array}{rl}{Z}_1(\omega )& =\sum _{n=0}^{N+M-1}z(n)e^{-\mathrm{j}\omega n}=\sum _{n=M}^{N+M-1}z(n)e^{-\mathrm{j}\omega n}\\ & =\sum _{i=0}^{N-1}z(i+M)e^{-\mathrm{j}\omega (i+M)}=\sum _{i=0}^{N-1}x(i)e^{-\mathrm{j}\omega (i+M)}\\ & =X_1(\omega )e^{-\mathrm{j}\omega M}\end{array}$$

$z(n)$的DFT为：

$$\begin{array}{rl}{Z}_2(k)& =\sum _{n=0}^{N+M-1}z(n)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}nk)=\sum _{n=M}^{N+M-1}z(n)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}nk)\\ & =\sum _{i=0}^{N-1}z(i+M)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}(i+M)k)\\ & =\sum _{i=0}^{N-1}x(i)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}ik)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}Mk)\\ & =\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}k)X_2(k)=\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N+M}}k)X_1(\omega ){\mid }_{\omega =2\pi \frac{k}{N+M}}\end{array}$$

通过对比可知，时域后面补零，相当于频域插值(频谱信息不变，但谱线密度变大了)。另外，时域前面补零，根据公式可知$z(n)$的DFT比$y(n)$的DFT多了相位因子，对应时域平移。

Y.2 时域内插0

设$x(n)$的长度为$N$，在$x(n)$的相邻样值间插入$L-1$个$0$，记新序列为$r(n)$，则插$0$后$r(n)$的长度为：$LN$

$r(n)$的DTFT为：

$$\begin{array}{rl}R(\omega )& =\sum _{n=0}^{LN-1}r(n)e^{-\mathrm{j}\omega n}=\sum _{n=mL}r(n)e^{-\mathrm{j}\omega n}\\ & =\sum _{m=0}^{N-1}x(m)e^{-\mathrm{j}\omega mL}\\ & =X_1(\omega L)\end{array}$$

$r(n)$的DFT为：

$$\begin{array}{rl}R(k)& =\sum _{n=0}^{LN-1}r(n)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{LN}}nk)=\sum _{n=mL}r(n)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{LN}}nk)\\ & =\sum _{m=0}^{N-1}x(m)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{LN}}(mL)k)=\sum _{m=0}^{N-1}x(m)\exp (-\mathrm{j}{\displaystyle \frac{2\pi }{N}}(m)k)\\ & =X_2(k)(k=0,1,2,\cdots ,LN-1)\end{array}$$

• 对比上述公式可知，发生了以下变化：
  • 原信号$x(n)$的频谱$X_1(\omega )$的周期为$2\pi$；内插$0$之后$r(n)$的频谱$R(\omega )$的周期为${\displaystyle \frac{2\pi }{L}}$；
    • 这也就是说时域内插$0$之后，频谱的周期宽度被压缩了$L$倍。
  • 同时可以发现$R(k)$包含了$L$个$X_2(k)$
    • 这也就是说时域内插$0$，相当于频域复制。

此外，时域内插$0$还可以理解为DFT的尺度变换性质：

$$r(n)=x(Ln)⟹R(k)={\displaystyle \frac{1}{|L|}}X\left({\displaystyle \frac{k}{L}}\right)$$

参考链接Y.1：关于频域补零（zero-pad），可以实现信号的时域内插的深刻理解？或者有这方面的详细资料吗？ - 严二姨的回答 - 知乎
参考链接Y.2：关于频域补零（zero-pad），可以实现信号的时域内插的深刻理解？或者有这方面的详细资料吗？ - Binfun的回答 - 知乎
参考链接Y.3：关于频域补零（zero-pad），可以实现信号的时域内插的深刻理解？或者有这方面的详细资料吗？ - 为何的回答 - 知乎
参考链接Y.4：实现时域内插可以fft、频域补零，再ifft，那么频域补零为何要在中间部位补零呢？ - 黑帅的回答 - 知乎
参考链接Y.5：对数字信号进行内插后（插0）再进行DFT得到的频谱会有什么变化？为什么？ - 大唐荣耀的回答 - 知乎
参考链接Y.6：对数字信号进行内插后（插0）再进行DFT得到的频谱会有什么变化？为什么？ - 星夜寒程的回答 - 知乎
参考链接Y.7：对数字信号进行内插后（插0）再进行DFT得到的频谱会有什么变化？为什么？ - 黑帅的回答 - 知乎
参考链接Y.8：数字信号处理中的内插、补零 - 博客园
参考链接Y.9：辨析改善频谱分辨率问题与栅栏效应——补零、插值、Zoom-FFT算法的影响（附Matlab仿真） - 坐看云起的文章 - 知乎
参考链接Y.10：FFT（快速傅里叶变换）时域/频域补零与补数据（内插、插值）对结果的影响，matlab实验，测试，有源代码 - CSDN
参考链接Y.11：大话数字信号处理——内插和抽取 - 风流中年的文章 - 知乎
参考链接Y.12：数字信号处理之内插 - CSDN
参考链接Y.13：第5章 信号的抽取与插值 - 人人文档
参考链接Y.14：信号的抽取与插值 - 人人文档
参考链接Y.15：信号的抽取与插值 - 豆丁文档
参考链接Y.16：DFT，DTFT，DFS，FFT之间的关系以及序列补零和插值对频域的影响 - CSDN
参考链接Y.17：上采的两种方法 - CSDN
参考链接Y.18：数字信号中的上采样和下采样 - CSDN
参考链接Y.19：【算法研究】 数字信号升采样(upsampling) 和降采样(downsampling) 技术 - CSDN
参考链接Y.20：DFT中人为地补零加长序列对频谱的影响？ - 杨树下的狐狸的回答 - 知乎
参考链接Y.21：DFT——末尾补零与插零方式的区别 - CSDN
参考链接Y.22：数字信号处理基础----信号的抽取和插值 - CDSN：包含带通采样定理！！！
参考链接Y.23：数字信号处理之信号的抽取和内插 - CSDN
参考链接Y.24：信号的采样与插值重建（包含matlab） - CSDN
参考链接Y.25：数字信号处理报告--升采样参考PPT - 百度文库

Z 弃置区（循环卷积/线性卷积，部分卷积/完全卷积）

关于fft那些简单却难的问题们 - CSDN

来自CSDN博主——暮霭露露——的文章，2022-04-15