最优化方法_Part3
10 对偶问题及强弱对偶定理
10.1 对偶问题的提出
-
如果原问题是非凸问题,那么将无有效的算法求解出它的全局解。一个顺其自然的想法就是构造一个与原问题紧密的问题,并且这个问题本身就很简单,而这个简单的问题就是这一节要讨论的对偶问题;
-
鲁棒优化、锥优化在某些情况下与对偶问题等价;
-
解出线性规划对应的对偶问题的最优解,可以得到原问题解的性质,并且对偶单纯形法比单纯形法效率更高;
-
通过对偶问题可以得到原问题最优解的下界。
10.2 对偶问题的构造
考虑如下约束问题
和前面的约束优化相比,原问题
对应的对偶问题
- 第一步:构造Lagrange函数
- 第二步:构造Lagrange对偶函数
- 第三步:构造对偶问题
10.3 原问题和对偶问题的关系
对偶问题
即对偶问题可以先看做是对Lagrange函数中的
对上式换一种形式:
做一个简单的分析
求最大值是很容易求到
- 如果不想取到
- 若要取到最大,则
对
在约束条件
又回到了原问题
交换下求最值的顺序即可得到原问题
因此原问题可以看做是对Lagrange函数先对
10.4 对偶间隙【对偶间隔】
原问题
10.5 弱对偶定理
10.5.1 弱对偶定理的描述及证明
设
弱对偶定理是天然成立的,由构造对偶问题的过程决定。
定理的证明:
记原问题
可以得到:
因此:
因为
即,
因此:
即:
10.5.2 弱对偶定理的推论
(一) 推论一
假设
证明:
因此
(二) 推论二
若
若
10.6 强对偶定理
先给出结论,强对偶定理即
10.6.1 几何解释
考虑简单的原问题
构造对应的对偶问题
- 第一步:构造Lagrange函数
- 第二步:构造Lagrange对偶函数
- 第三步:构造Lagrange对偶问题
记:
则将
对偶问题
其中,
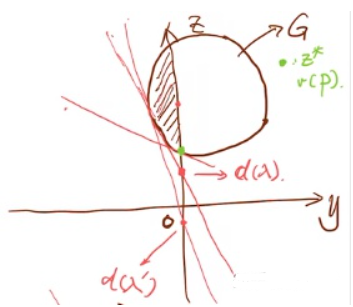
如果
则
10.6.2 强对偶定理的描述及证明
(一) 强对偶定理的描述
集合
存在
且
则强对偶成立:
(二) 定理中条件的说明
要求原问题
存在

集合图像理解很容易可以得出找不到最优解的结论
定理的证明(TODO):需要利用凸集的性质,目前这块学的不好,待补充。
本小节参考资料:
【1】如何通俗地讲解对偶问题?尤其是拉格朗日对偶lagrangian duality? - 李竞宜的回答 - 知乎
【2】拉格朗日乘子的几何解释
10.7 对偶问题的性质及求解办法
10.7.1 对偶问题的性质
(一) 对偶函数一定是凹函数
证明过程:为什么拉格朗日对偶函数一定是凹函数;该博客介绍的很详细,包括不等式如何过去,比书本要好多了。
(二) 对偶问题是凸优化问题
已知对偶函数
因为对偶函数是凹函数,对凹函数求最大相当于凸函数求最小,问题等价于:
因此对偶问题是凸优化问题。
10.7.2 对偶问题的求解
(一) 特殊问题对偶问题的求解
-
如果原问题
-
如果原问题
-
如果如果原问题
(二) 一般问题对偶函数的求解
一般形式的函数的对偶问题将无法使用上述提到的方法,对于一般函数的对偶问题的求解有专门的方法,比较常见的是
- 割平面法又称为外逼近法【cutting plane method】
- 次梯度法【subgradient method】
- bundle method
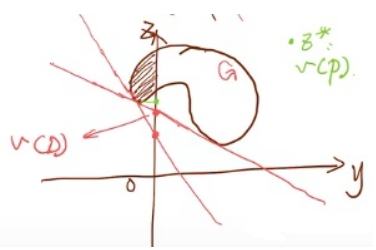
(三) 几何解释
先对问题做一个化简,记
则对偶问题
其中,
记最优解为
假设
问题变为了一个线性规划问题,可以通过单纯形法或内点法进行求解,也可以借用软件cplex进行求解,但是当
考虑

可以发现起约束作用的直线只有三条,另外两条不起作用。当
还是以
因此对偶问题
记现问题的最优解为
两个方程,两个未知量可以解出
解得最优解为
-
若
-
若
如果上面两种情况都不满足的话,说明选取的点不够好,近似效果不行,需要重新选取点。一般重新选取点是将最优解
(四) 外逼近法算法实现
前面已经图文并茂的介绍了外逼近方法,这里给出算法的具体实现思路,有了前面的讲解后将非常容易的理解
-
STEP 1:选取
-
STEP 2:求解线性规划问题
-
STEP 3:求解相应的子问题
-
STEP 4:
- 情况1 —— 若
- 情况2 —— 若
- 情况1 —— 若
-
STEP 5:
(五) 其他说明
-
-
算法的缺点:在最优解的位置具有不稳定性,无法判断解的最优性。
11 线性规划
11.1 线性优化研究的问题
线性优化研究的问题具有以下特点:
-
目标函数为决策变量的线性函数
-
约束条件为线性等式或线性不等式约束
11.1.1 线性优化的标准型
线性优化问题的标准型具有以下形式,记该问题为
其中,
11.1.2 非标准型和标准型之间的转换
并非所有的线性优化问题都是标准的线性优化问题,但是只要是线性优化问题就一定可以化为标准型。
- 不是求解最小值问题,转换形式如下:
- 约束条件为不等式,转换形式如下:
其中,
- 决策变量无符号要求,转换形式如下:
11.2 可行集与多面体的性质
11.2.1 可行集
线性优化的可行集:
并且可行集是一个多面体。
11.2.2 多面体的性质
-
极点(extreme point):给出凸集
-
方向(recession direction):给出凸集
-
极方向(extreme direction):若方向
11.3 极点的刻画
11.3.1 定理
考虑多面体
说明:
记
因此如果给了
因此
又知
可得方程的一个解为
后面的定理中将不再说明矩阵
11.3.2 证明
证明略,具体参考视频和转载的知乎笔记。
11.4 方向的刻画
若
因为
由
且满足
11.5 极方向的刻画
11.5.1 定理
考虑多面体
其中,
说明:
11.5.2 证明
略,具体证明过程请参考视频和转载笔记。
11.6 可行集的其他表示
可行集的表示除了
其中
即可行集中的点可以表示为极点的凸组合加极方向的非负组合,这个定理结合图形很容易理解,这里暂时不做证明。
11.7 单纯形法
因为可行集有另外一种表示,因此问题
即
当选取了极点和极方向以后,问题就转换为了关于
-
若存在某个
-
若
因此最小值在极点处取到;即线性优化问题
如果极点非常多,一个一个将极点带进去进行比较求最小,时间成本将非常高,因此就有了单纯形法。单纯形法的基本思想是找到找到一个极点
11.7.1 如何判断最优解
取
因此
解得
若对
因为
若
11.7.2 如何选取下一个极点
若
则
记
如果
优化问题无解。
如果
恒成立。因为
即
因此每个分量都需要大于等于0,即
即
可以得到
因此
下一个更优的极点为
总结:
若从
12 等式约束的二次规划问题
12.1 等式约束的二次规划问题描述
考虑如下的等式约束的二次规划问题
也可以写为:
其中,
假设
12.2 等式约束求解方法
12.2.1 KKT法
(一) KKT法的原理
因为问题
将KKT条件写成矩阵乘积的形式,即:
若
(二) KKT法的缺点
当
12.2.2 变量消去法
(一) 变量消去法的原理
为了克服KKT法的缺点就有了变量消去法,所谓变量消去法就是将
和线性优化中相同的处理方式,对矩阵
其中,
因此上述等式二次规划问题等价于:
因为
又因为矩阵
将
可以理解为
将
记
则转换为对应的无约束优化问题为:
若
解得:
因此:
即为问题
得到:
由于
(二) 变量消去法的优缺点
-
方法的优点:
- 直接消去法简单、直观。
-
方法的缺点:
- 当
- 当
13 不等式约束的二次规划问题
上一节学习了等式约束的二次规划问题,介绍了变量消去法和KKT法两种求解的方法,但是一般的求解问题中都是带有不等式约束的,因此这一节将学习不等式约束的二次规划问题。
13.1 一般的二次规划问题
前面介绍了等式约束的二次规划的求解方法,求解的问题有可能是带有不等式约束的,考虑如下问题,记为
13.2 最优解的性质
性质一:最优解为KKT点。
性质二:假设
则
性质2证明:
因为
由互补松弛条件可知:
因此,上式的
因此上述KKT条件可以改写为:
即问题
由一般的二次规划问题的最优解可求等式约束的二次规划问题的最优解,等式约束的二次规划问题很容易可以通过变量消去法、零空间法或KKT法求得。很容易想如果知道了问题
13.3 定理
13.3.1 定理内容
设
得
13.3.2 定理证明
证明暂略,请参考视频讲解或者转载的笔记。
13.4 有效集法思路
有上述的定理就会想,如果对应的
假设
的最优解为
13.4.1 情况一:
-
若
-
若存在
13.4.2 情况二
-
若
-
若
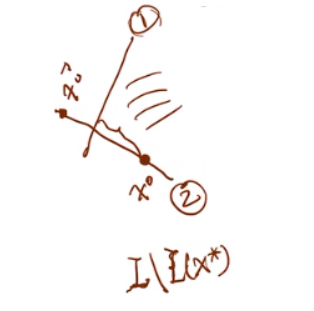
比如图上的
其中对条件
做一个变形得:
如果
因为
不等式天然成立,现考虑
则
最优解在等号处取得,记
构造新的迭代点
及可行集
在求解对应的二次规划问题,直到情况一的1成立
13.5 有效集法算法梳理
前面已经很详细的介绍了有效集方法的实现思路,这里给出具体的算法步骤
-
STEP 1:给定问题
-
STEP 2:求解下面对应的等式二次规划问题
-
STEP 3:若
-
STEP 4:若
- 情况1:
- 情况2:
- 情况1:
其中,
转STEP 2。
【1】数值优化| 对偶问题及强弱对偶定理,数值优化 |对偶问题的性质及求解办法
【2】最优化| 线性优化
【3】数值优化| 不等式约束的二次规划问题
【4】数值优化| 等式约束的二次规划问题
【5】数值优化| 不等式约束的二次规划问题

 最优化方法基础知识👉第三部分
最优化方法基础知识👉第三部分


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 上周热点回顾(3.3-3.9)
· AI 智能体引爆开源社区「GitHub 热点速览」
· 写一个简单的SQL生成工具