高等数学_Part1
1 极限
微积分,既是一种工具也思想。方法虽看似繁多其实背后蕴含的道理浅显而直观莫要迷失于众多的题目中,关键在于体会方法背后的想。
1.1 认识极限

极限式如
1.2 理解极限
极限过程是一个动态的过程,不是一个“死”的数字。而至于“
1.3 求函数极限
1.3.1 求解函数极限
- 第一步,代入:将自变量极限值代入极限表达式,如果不能得到结果,继续下一步;
- 代入时,需要注意三点问题:① 无穷大与无穷小之间呈倒数关系;② 无穷小×有界函数=无穷小;③ 需要注意极限的方向性问题,区分“
- 代入时,需要注意三点问题:① 无穷大与无穷小之间呈倒数关系;② 无穷小×有界函数=无穷小;③ 需要注意极限的方向性问题,区分“
- 第二步,分类:判断极限类型属于“
- 第三步,求解:根据极限类型,选择分别适用的求解方法,进行化简或者变形。
1.3.2 无穷小相关的极限问题 ——
对于无穷小相关的极限,可采用的方法有:
- 1° 化简:消除“致0因子”;
- 2° 等价无穷小代换;
- 3° 洛必达法则。
常用的等价无穷小代换:当
| 原函数 | 等价无穷小 |
|---|---|
Tips:函数
如果过原点,即 ,而且导数有 ,则在 时, 可以和 等价无穷小代换(泰勒展开)。
使用等价无穷小代换时,需要关注以下2个细节:
- 要学会“抓住”无穷小,如果
- 两个无穷小量相加减时,不可将其中任意一个部分进行代换。(但是我们可能会发现有一些替换了其中一个部分,这是因为利用了极限的运算法则,需要满足运算法则的前提条件)
此外,论文中会出现式子计算过程中,某一部分突然没有了,这可能就是因为消失的那一部分是前面某个项的高阶无穷小,可以直接忽略掉。
1.3.3 无穷大相关的极限问题 ——
解决无穷大类型问题的方法:“抓大头”的思想理念,抓住主要矛盾,忽略次要成分:
当两个相差无穷倍的量相进行加减时,这时候我们眼里可以忽略相对较小的一个量。在具体操作上,应该将最大的成分提括号外,分子分母同时除掉即可。
1.3.4
方法1:利用特殊极限
方法2:利用等式
小tip:当底数和指数都有变量时,通常使用
、 变换。
1.3.5 极限运算法则
如果函数
在处理极限的时候,我们可以选择将极限进行部分地运算。但要尤其注意前提条件!
2 函数的连续性与间断点
2.1 连续性与间断点
2.1.1 函数可微性
- 一元函数的可微性(注意,暂时不考虑多元函数)
设函数
如果存在常数
则称函数
由定义可见,函数的微分与增量仅相差一个关于
容易看出,一元函数
一元函数可微的充要条件:函数
2.1.2 函数的连续和可导性
-
怎么判断一个函数是否连续和可导?
- 连续:函数在某点连续<==>函数在该点左极限等于右极限等于该点函数值;
函数
①
②
③注意:可去间断点并不是函数连续,连续的定义是左右极限都存在并且都等于那一点的函数值,可去间断点并没有后面那一条(可去间断点左右极限值是存在且相等,但是极限值≠函数值)。
- 可导:函数在某点可导<== >函数在该点连续,且其导函数在该点连续。
- 1、导数无穷大,属于不可导的情况之一。就和极限无穷大属于极限不存在的情况之一一样。
- 2、对于一元函数而言,不连续的点必然不可导,这点可以直接从导数的定义公式中得出结论。
- 3、不可导的情况有:
- 1)左右导数中至少有一个是无穷大(含+∞和-∞)
- 2)左右导数都存在,但是不相等。
- 3)各种各样的不连续点,无论是可去间断点、跳跃间断点、无穷间断点,无限震荡间断点,都是不可导的。
2.1.3 函数的间断点
函数连续性应满足条件:

通过计算

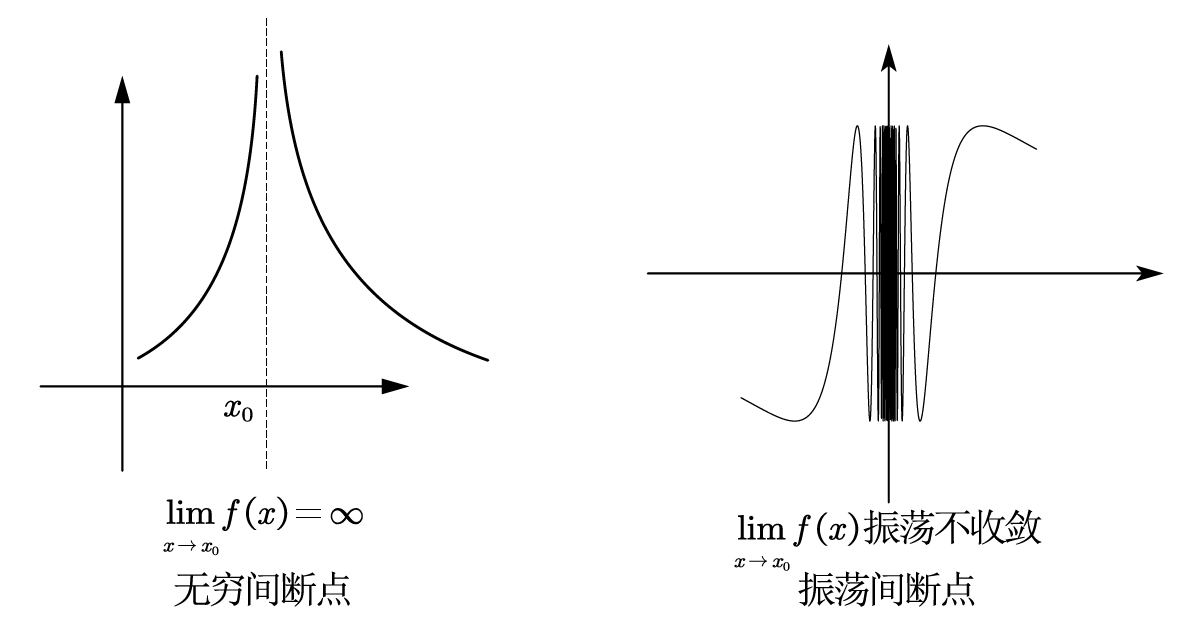
总结:

2.2 函数连续,可导,可微和偏导数连续的关系
2.2.1 一元函数
- 可导与连续的关系:可导必连续,连续不一定可导;
- 可微与连续的关系:可微与可导是一样的;
- 可积与连续的关系:可积不一定连续,连续必定可积;
- 可导与可积的关系:可导一般可积,可积推不出一定可导;
2.2.2 多元函数
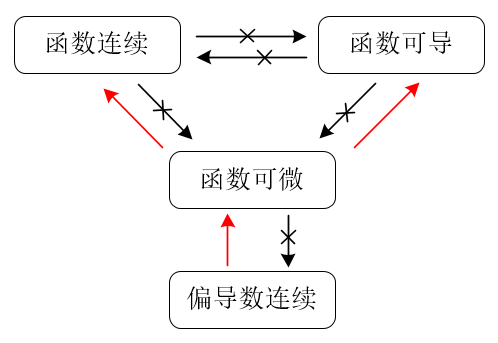
函数连续不一定的函数可微(例子:
函数连续不一定函数可导(例子:
函数可导不一定连续;
可导指的是偏导数存在,即沿
3 微分
3.1 导数的定义
直线的斜率
(1)
(2) 反映出直线的坡度:直线与
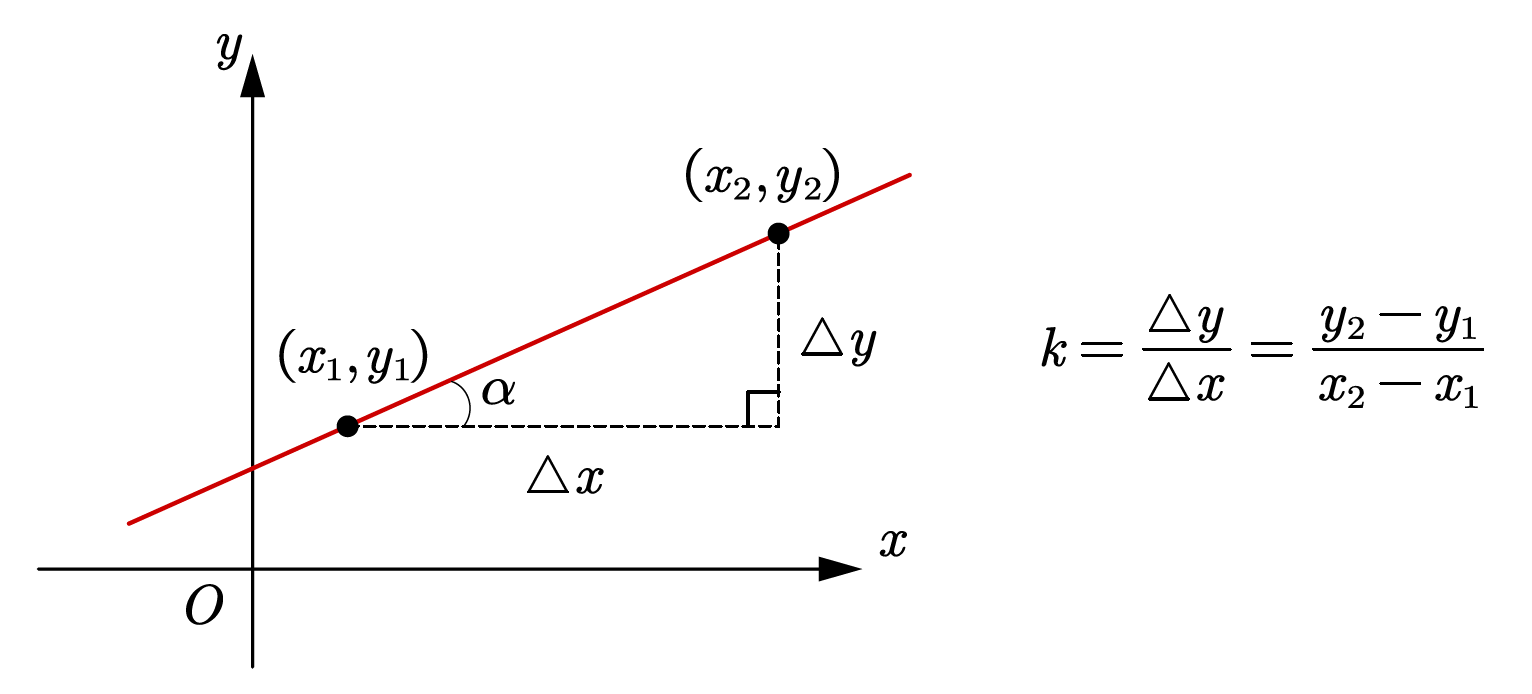
如何研究曲线中
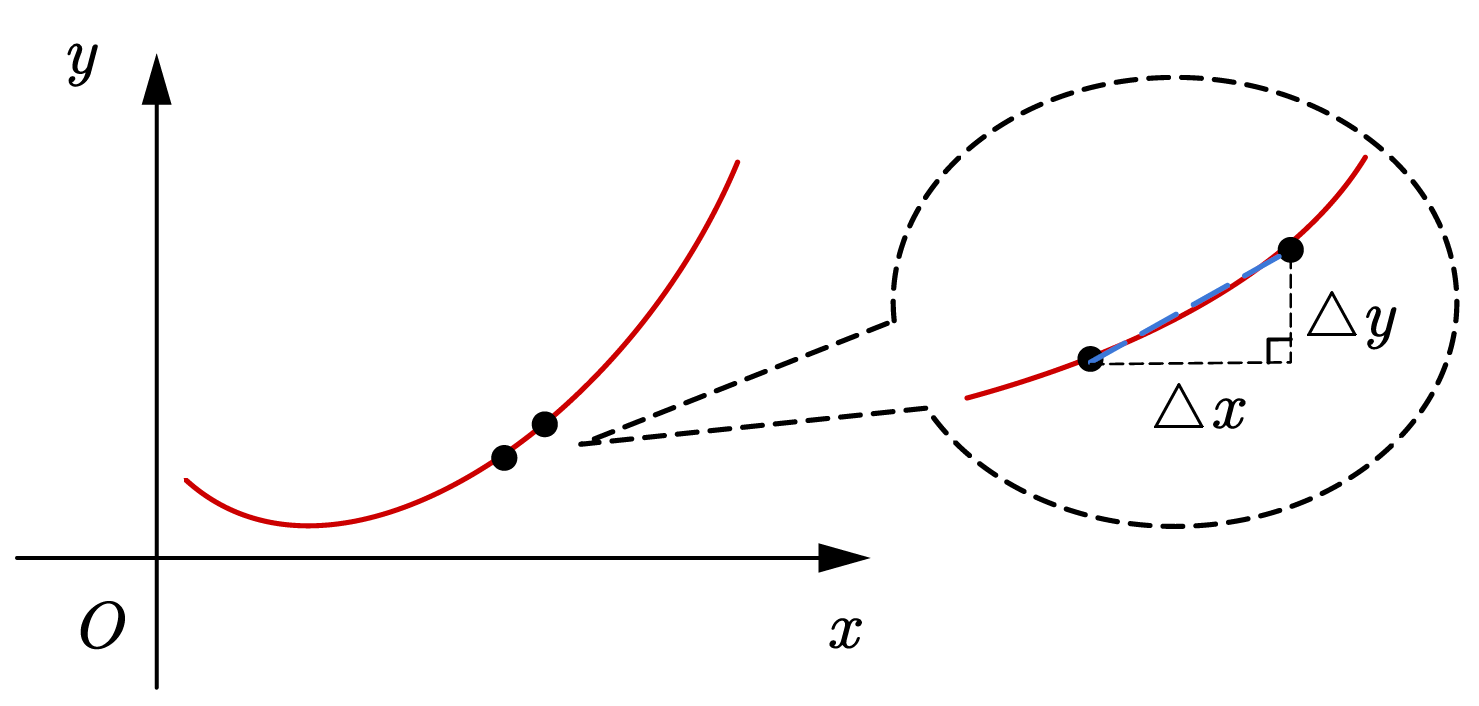
导数反映出因变量随着自变量增长而变化的快慢。导数定义如下:

导数也被叫做“微商”,可以理解为两个无穷小量之间的比值。
3.2 导数的基本运算
3.2.1 常用函数的导数
3.2.2 导数四则运算法则
3.2.3 复合函数求导
3.2.4 求导链式法则
即设置中间变量:
3.2.5 莱布尼茨公式
设
如果函数
掌握莱布尼茨公式并不难,它类似于我们高中的“二项式定理”。
3.2.6 隐函数求导
隐函数,例如:
3.2.7 参数方程求导
形如
3.3 泰勒公式
泰勒级数:只要一个函数无穷光滑,那么泰勒级数就存在,但是不一定收敛,而且即使收敛,也不一定收敛于原函数。
泰勒公式:就是会有余项,多用在极限计算和中值定理,应用的条件只要函数在待考察的区间上有
泰勒展开式:泰勒展开式的方向是从函数变成级数,而且要求级数必须收敛,并且必须收敛于被展开函数在对应点所取到的函数值。所以会有收敛域。
3.3.1 泰勒级数定义
如果
称为
3.3.2 泰勒公式定义
若函数
这是一个有限项的求和,所以不存在收不收敛的问题,而余项
- 最简单的是佩亚诺余项:
- 拉格朗日余项:
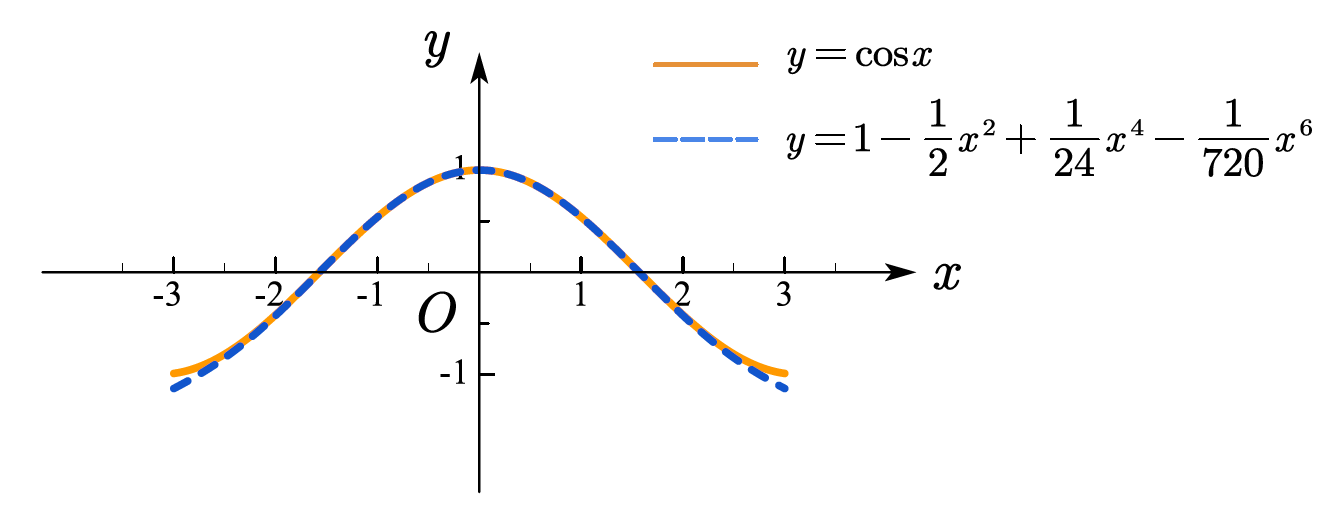
泰勒公式就是把
我们需要把握下列常见函数的泰勒展开(麦克劳林展开,佩亚诺余项)形式:
- 泰勒公式的要点:
(1) 上述是在
(2)
(3) 利用导数、原函数的关系,就可以辅助记忆,例如
(4) 泰勒公式可以将复杂的函数计算化简成为加减乘除;
(5) 泰勒公式具有拓展性,当
对进行替换,例如:
3.3.3 泰勒展开式(泰勒级数)
(注意泰勒级数是一个有无穷项求和的函数项级数,它可能不收敛或者只在某些区间收敛,而且就算它收敛,它的和函数也不一定等于原函数!)这个会有收敛区间,这个就是其和泰勒公式的区别,比如
总之,可以记住一点,级数是无穷级数的简称,谈论到级数一定是无穷项的,而且讨论级数一定要讨论级数收敛的条件,即收敛半径、收敛域。
3.3.4 泰勒公式的应用
(1) 利用泰勒公式求极限
泰勒公式可以看作是超级版本的无穷小代换,它不会受到加减法不能换的限制。
(2) 判断无穷小的阶数
(3) 求高阶导数
3.3.5 泰勒展开与泰勒级数
泰勒展开公式的余项是抽象的,就是说泰勒展开公式是一种拟合。泰勒级数的表达是唯一确定的。任何函数都有泰勒展式,但不一定能展成泰勒级数。当泰勒余项能用省略号表示的时候(即泰勒余项和无穷级数的后面的无穷多项相等),函数可以展成泰勒级数,具体就是泰勒余项在
3.3.6 泰勒级数相关资料
泰勒级数推导
ln x泰勒展开不相等
不同余项型泰勒公式的证明与应用
4 积分部分
4.1 积分的基本概念:定积分和不定积分
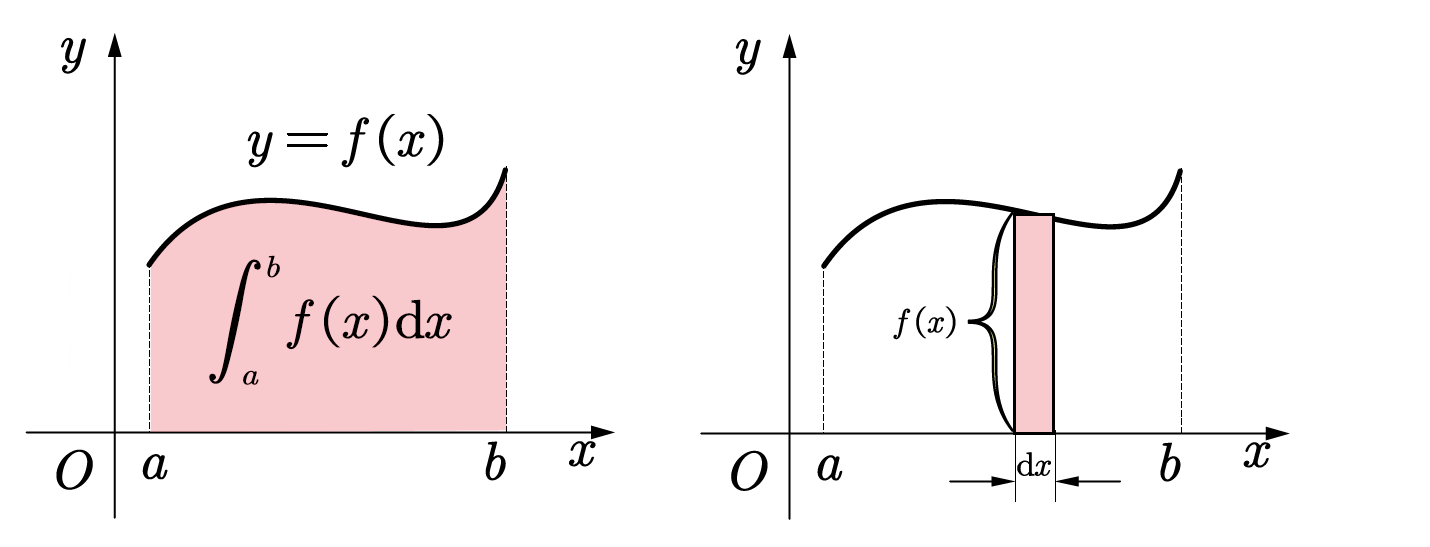
例如求
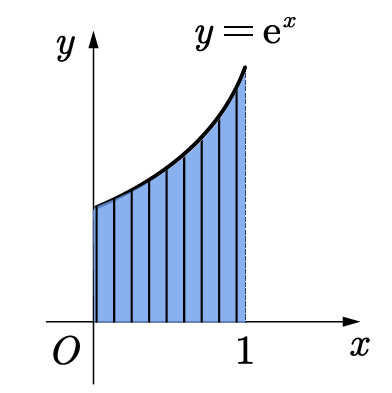
假设把
微积分最为核心的公式 —— 牛顿-莱布尼茨公式:
其中函数
为
4.2 常见函数积分
需要注意的是,求不定积分一定要在表达式结尾“
4.3 积分运算法则
4.4 常见求积分类型
4.4.1 积分的线性变换
被积函数是
4.4.2 凑微分法:要求熟练掌握各类导数
三角积分函数中的凑微分法小技巧,若积分式
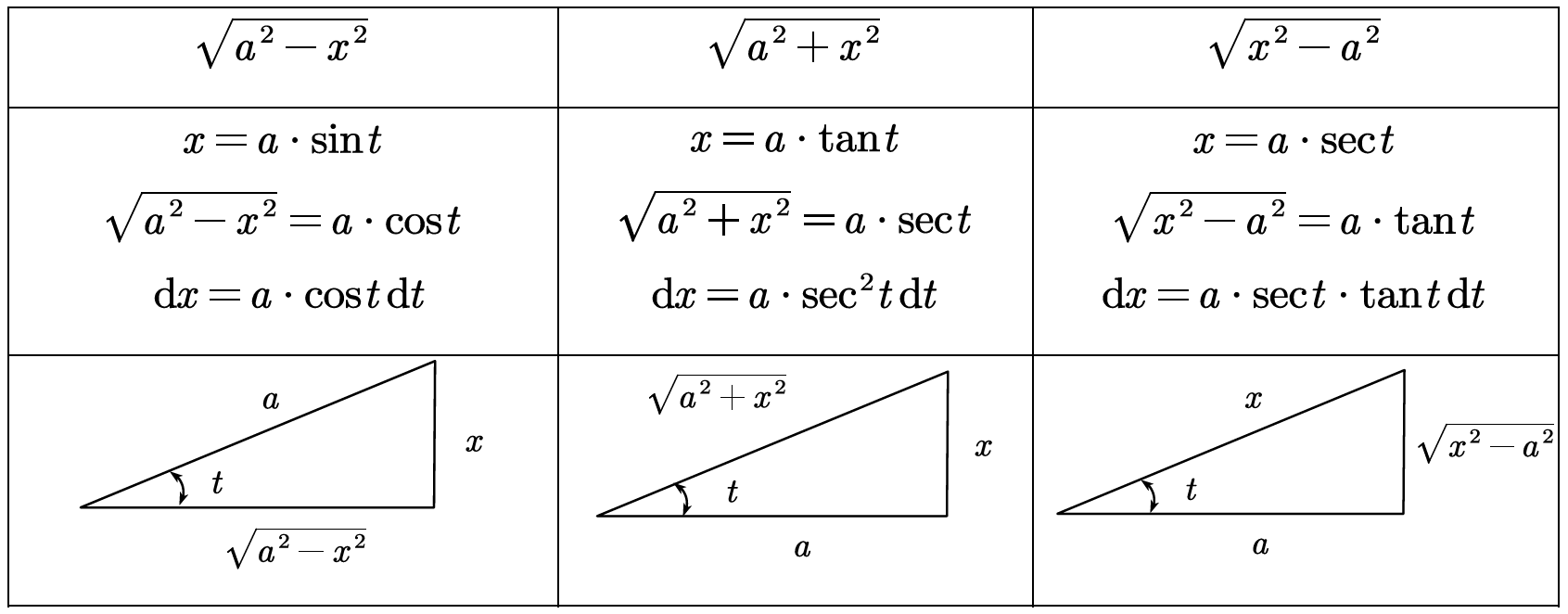
4.4.3 根式/三角变换
换元目标:消除根号。
- 第一类:根号内为
- 第二类:根号内为
4.4.4 分部积分法
引入例题:求下面图示阴影区域的面积:
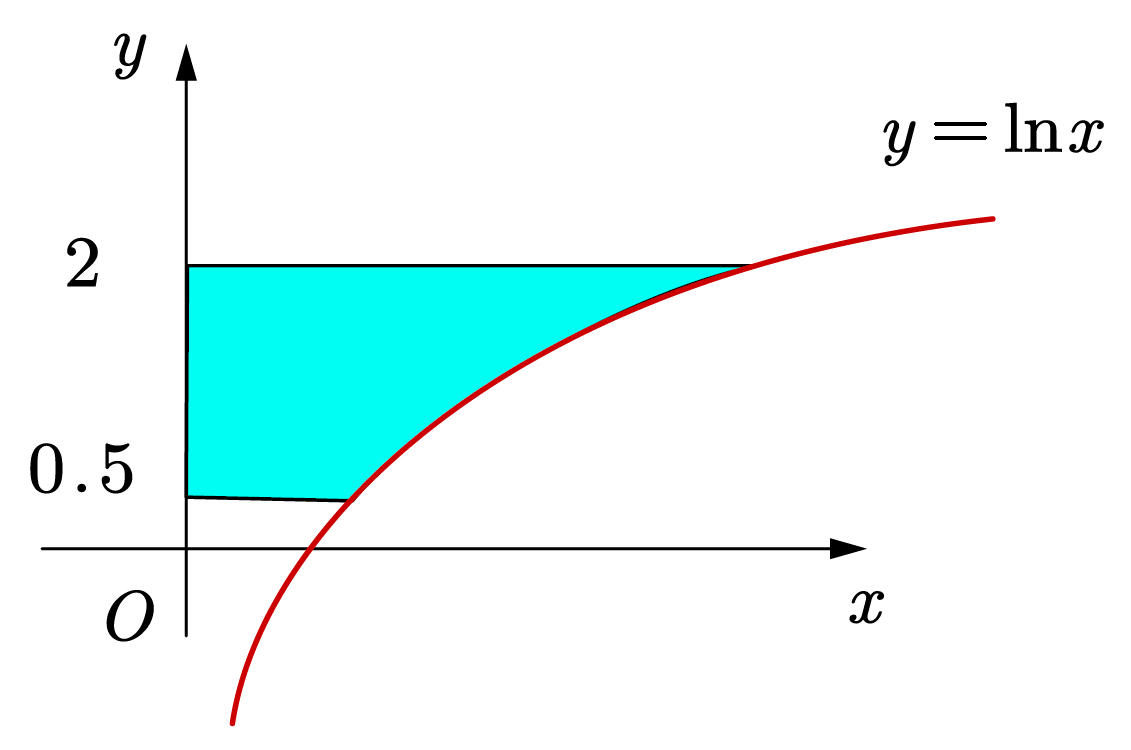
由于
由此可以推导得到分部积分的原理与公式:
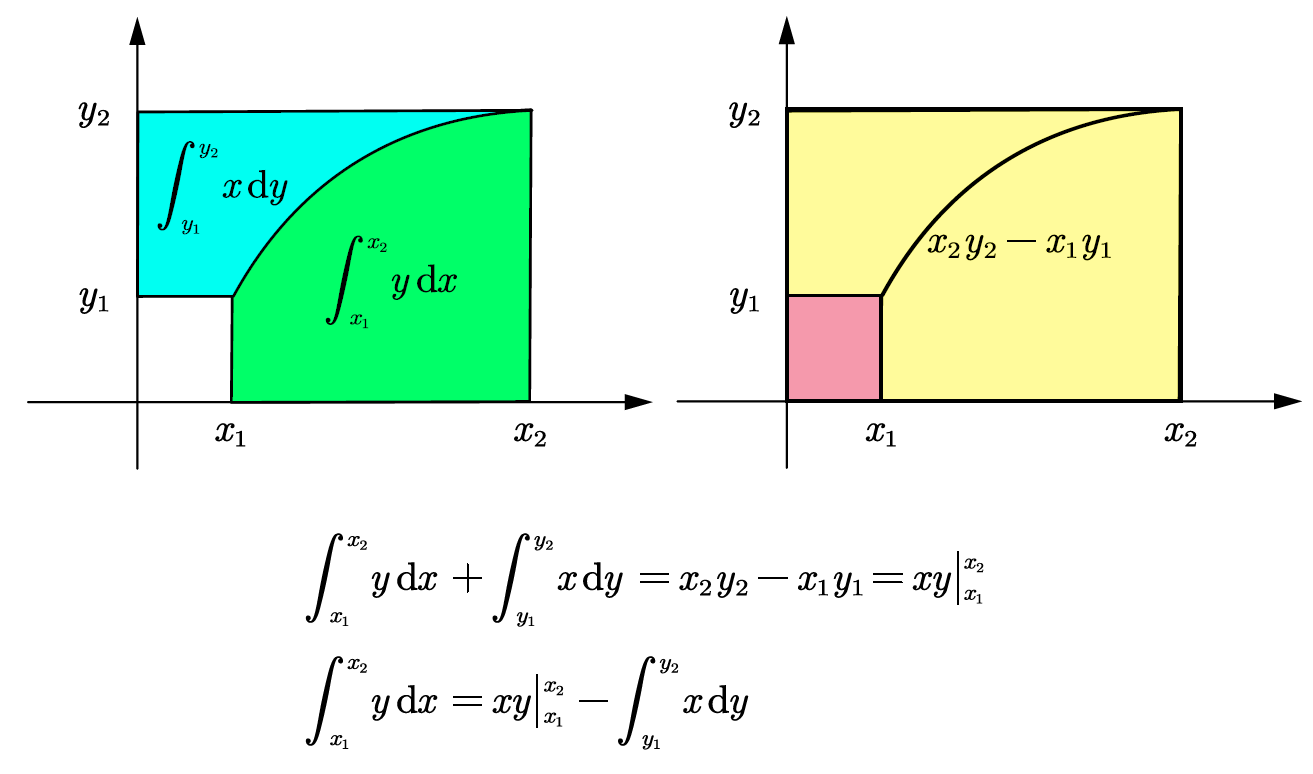
被积函数为两种不同类型函数相乘时,一般用分部积分法。
记住口诀:反对幂指三(反三角函数、对数函数、幂函数、指数函数、三角函数)。
口诀中,越是靠后类型的函数,越优先与“
4.4.5 变限积分
对于变上限积分函数,我们常用到的是它的导数:
而这种题目有相应的变体,我们也需要掌握:
4.5 定积分运算
定积分与不定积分类似,也需要求函数的原函数。但是不同的是定积分指定了上、下限,在求得原函数后需要代入、作差,例如
相比于不定积分,定积分还需要格外注意在引用新字母进行换元方法时,上下限也需要更换。
5 中值定理
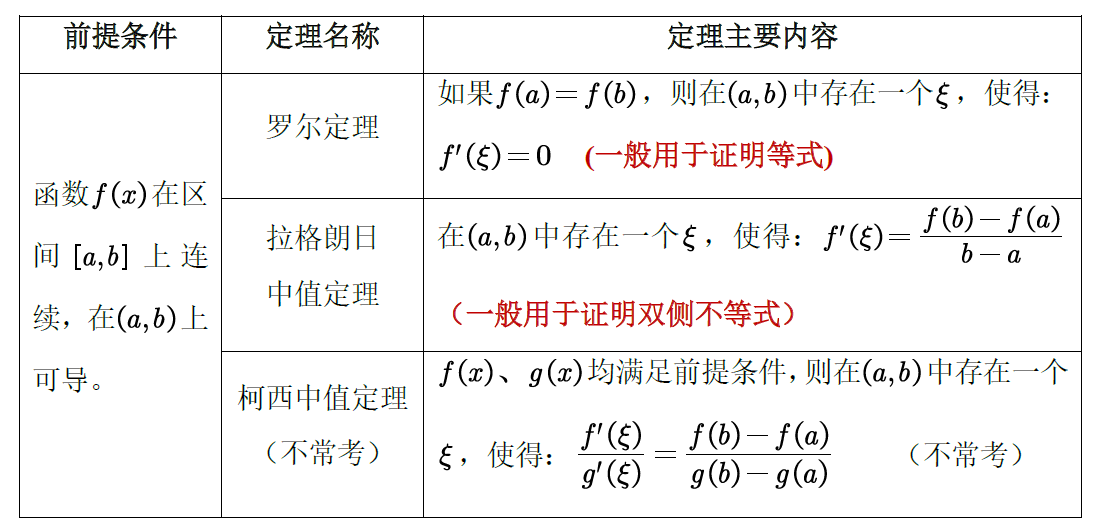
5.1 罗尔中值定理证明等式
从图像上理解罗尔/拉格朗日中值定理:
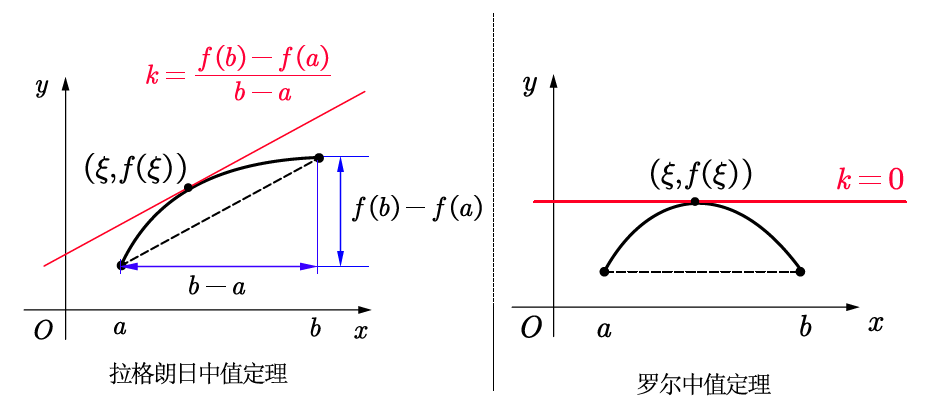
第一步:将需要证明的等式中的“
第二步:需要构造辅助函数
第三步:结合题目给出的其他条件,在区间
此类题目的难点无非两点:构造辅助函数,证明两处值相等。
5.2 数列极限
5.2.1 直接化简法
5.2.2 利用夹逼准则(缩放)
5.2.3 转化为定积分
导数dy/dx理解(除法?)
泰勒展开
高阶无穷小削去
本文参考资料:
课程链接:https://www.bilibili.com/video/BV1j44y1E7ot
PDF资料链接:https://pan.baidu.com/s/1ZD6Qj9R0VycOF4S0SMYY1w 提取码:gb6s

 高等数学基础内容简要回顾👉第一部分
高等数学基础内容简要回顾👉第一部分


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通