双曲型偏微分方程的几个概念

本章研究了一类双曲型偏微分方程的一些基本性质。
本书中研究的离散化技术主要基于偏微分方程的基本物理和数学特性。因此，有理由在偏微分方程的一些基础上投入一些精力。这里我们几乎只讨论双曲偏微分方程，特别是双曲守恒律。这主要有三个原因：
（i）当忽略粘性和热传导的影响时，可压缩流体流动方程简化为双曲方程组，即欧拉方程。
（ii）从数学上讲，通常认为流体流动的偏微分方程的双曲项是对离散化技术提出最严格要求的项。
（iii）双曲系统理论比更完整的数学模型（如Navier-Stokes方程）要先进得多。
此外，近年来，以双曲型问题为主题的研究和发展活动明显增加，因为这些活动涉及广泛的科学和技术领域。
我们仅限于双曲偏微分方程的一些基础知识，并选择了一种非正式的表达方式。所选择的主题和方法几乎完全受本书主题的启发，即黎曼问题和高分辨率迎风和中心数值方法。

拟线性方程组：基本概念

如果矩阵A的元素aij都是常数，并且向量B的分量bj也是常数，则系统（2.2）是具有常数系数的线性系统。
如果aij＝aij（x，t）并且bi＝bi（x，t），则系统是具有可变系数的线性系统。
如果B线性地依赖于U，则系统仍然是线性的，如果系数矩阵A是向量U的函数，即A=A（U），则系统被称为拟线性的。注意，拟线性系统是非线性方程组的一般系统。如果B=0，则系统（2.2）称为齐次系统。
对于形式（2.2）的一组偏微分方程，需要指定自变量x和t的变化范围。通常，x位于实数的子区间，即xl<x<xr；这个子区间被称为偏微分方程的空间域，或者仅仅是域。在值xl、xr时，还需要指定边界条件（BCs）。在本章中，我们假设域是全实域，-∞＜x＜∞，因此不需要指定边界条件。关于时间t的变化，我们假定t0<t<∞。初始条件（IC）需要在初始时间指定，通常选择t0=0。

守恒律与雅可比矩阵

守恒律可以写成拟线性形式

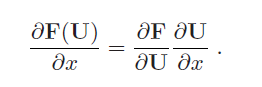
系数矩阵的特征值和特征向量

特征值物理上代表波传播的速度

双曲系统，严格双曲系统与椭圆系统

如果A具有m个实本征值λ1，…，λm和相应的一组m个线性独立的右特征向量K（1），K（m），则称系统（2.2）在点（x，t）处是双曲的。如果特征值λi都是不同的，则称该系统是严格双曲型的。注意严格的双曲性意味着双曲性，因为实的和不同的特征值保证了一组线性独立的特征向量的存在。
如果a的特征值λi都不是实的，则称系统（2.2）在点（x，t）处是椭圆的。

线性对流方程

特征线和通解

我们记得在标量方程的背景下对特征或特征曲线的定义，如（2.32）中的定义。特征线可以定义为t–x平面中的曲线x=x（t），PDE沿着该曲线成为ODE。
考虑x=x（t），并将u视为t的函数，即u=u（x（t，t）。
u沿x=x（t）的变化率为

因此，如果u在时间t=0时被赋予初始值u（x，0）=u0（x），那么沿着穿过x轴上初始点x0的整个特征曲线x（t）=x0+，解为u（x、t）=uO（x0）=uo（x−at）。(2.39)
对（2.32）中PDE的解（2.39）的解释是：给定初始轮廓u0（x），如果a>0，PDE将简单地将该轮廓以速度a向右平移，如果a<0，则向左平移。初始轮廓的形状保持不变。所研究的（2.32）中的模型方程包含了波传播现象的一些基本特征，其中波被理解为以有限速度传播的扰动的一些可识别特征。

黎曼问题

现在我们研究一个特殊的IVP（initial value ploblem)，称为黎曼问题

黎曼问题的解可以在x–t平面上表示，如图2.3所示。通过x轴上的任何点x0，都可以绘制出一个特征线。由于a是常数，这些都是相互平行的。对于黎曼问题的解，通过x=0的特征线是典型的。这是唯一一个两侧解发生变化的特征线。

线性双曲系统

在前一节中，我们详细研究了最简单的双曲型PDE，即具有恒定波传播速度的线性对流方程的行为和一般解。这里我们将分析推广到形式为m个双曲偏微分方程的集合

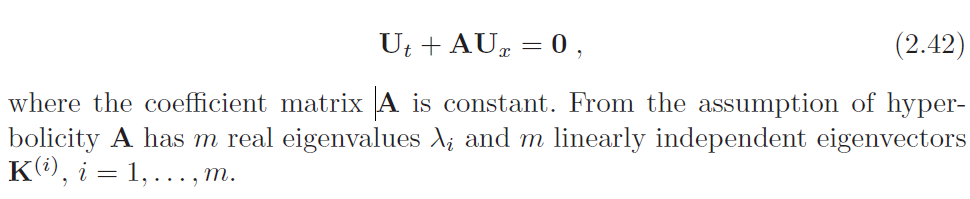
为了分析和求解（2.42）的一般IVP，发现将因变量U（x，t）转换为一组新的因变量W（x，t）是有用的。为此，我们回顾以下定义

特征变量

U的解（2.53）可以看作是m个波的叠加，每个波独立地平流而不改变形状。第i个波的形状为wi（0）(x）K（i），传播速度为λi。

常系数矩阵双曲系统的黎曼问题

守恒定律的积分形式

守恒定律可以用微分和积分形式表示。考虑守恒定律的积分形式有两个很好的理由:（I）控制方程的推导基于物理守恒原理，表示为控制体积上的积分关系，（ii）积分公式对解的光滑性要求较低，这为扩展允许解的类别以包括不连续解铺平了道路。
考虑一个一维时间相关系统，如一维欧拉方程，在x–t平面上选择一个控制体积V =【xL，xR】×【t1，t2】，如图2.10所示。

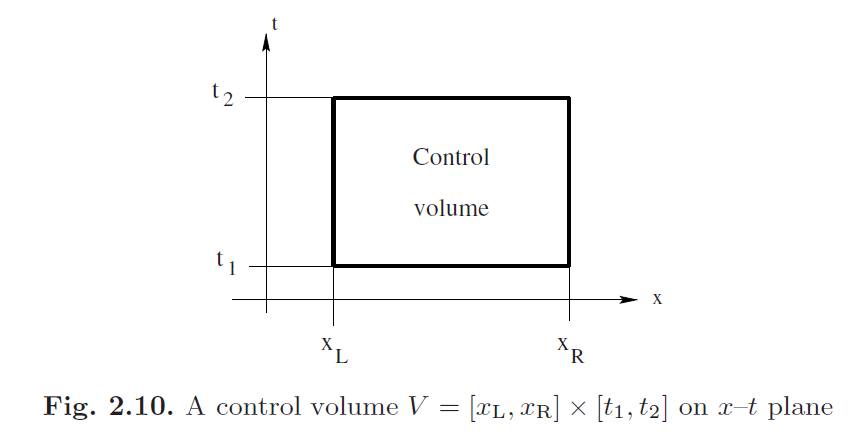
一维质量守恒方程的积分形式

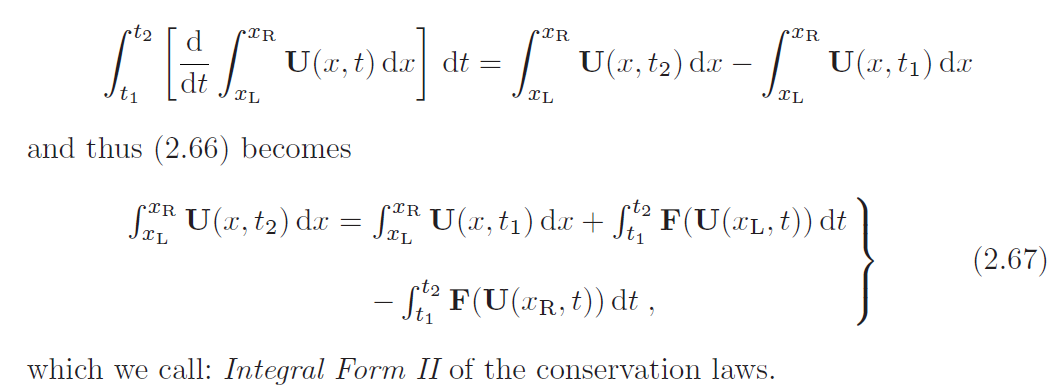
非线性与激波形成

在这里，我们研究非线性双曲守恒定律的一些显著特征，例如波变陡和激波形成。我们只关注标量非线性守恒律的初值问题

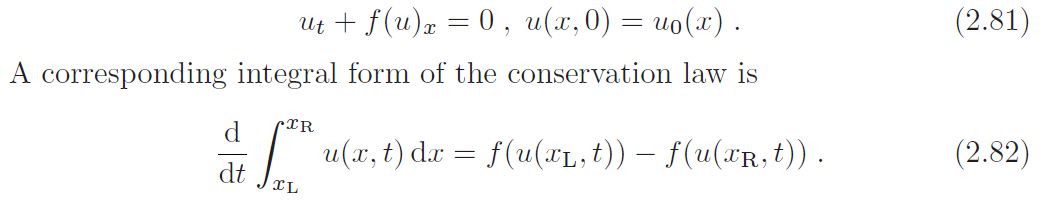
通量函数f被假设为仅是u的函数，在某些情况下，这不足以代表所模拟的物理问题。我们感兴趣的相关物理现象是可压缩介质中的冲击波。除了纯对流之外，它们还有粘性耗散和热传导。模型守恒定律更合适的通量函数还包括对u对x的导数的依赖，因此修改后的守恒定律为

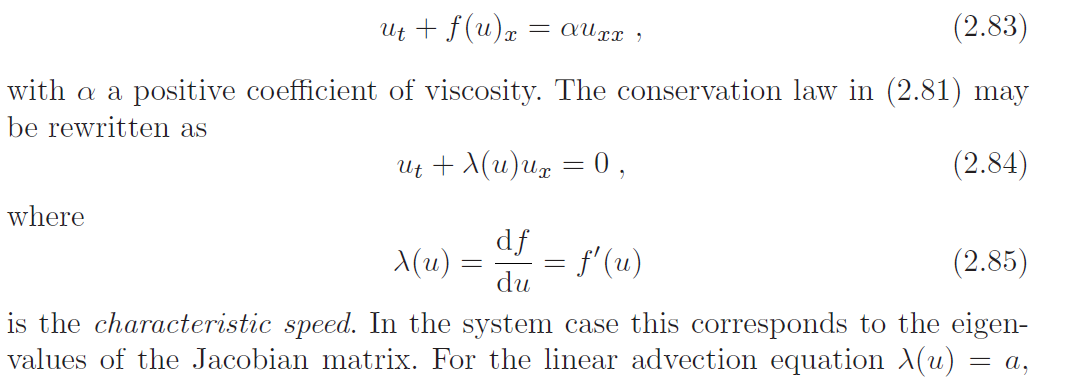
通量函数f（u）的行为对守恒定律本身的解u（x，t）的行为有深远的影响。一个重要的性质是特征速度λ（u）的单调性。基本上有三种可能性

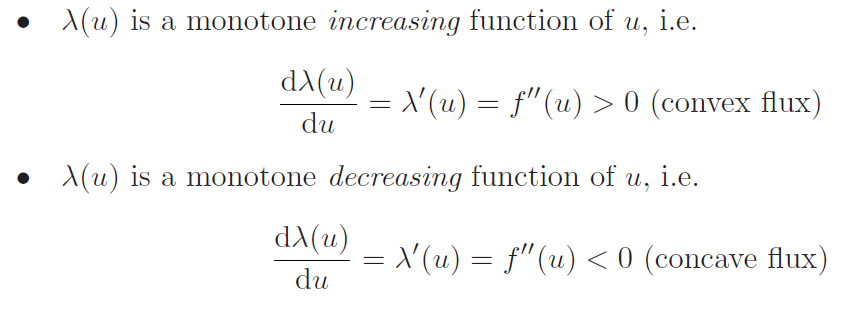
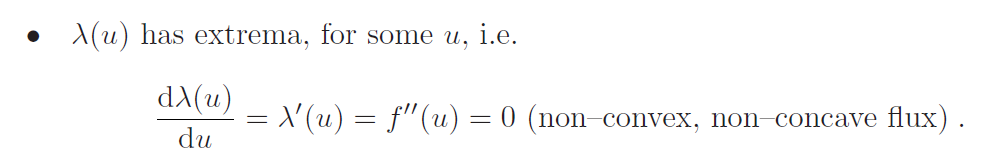
在非线性守恒定律系统的情况下，通量函数的特征由状态方程决定。人们谈到凸的或其他的状态方程

在特征线上构造解

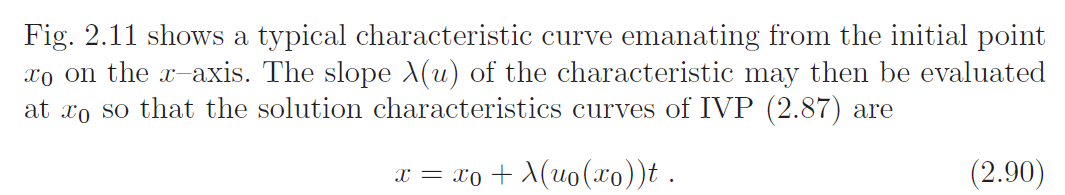
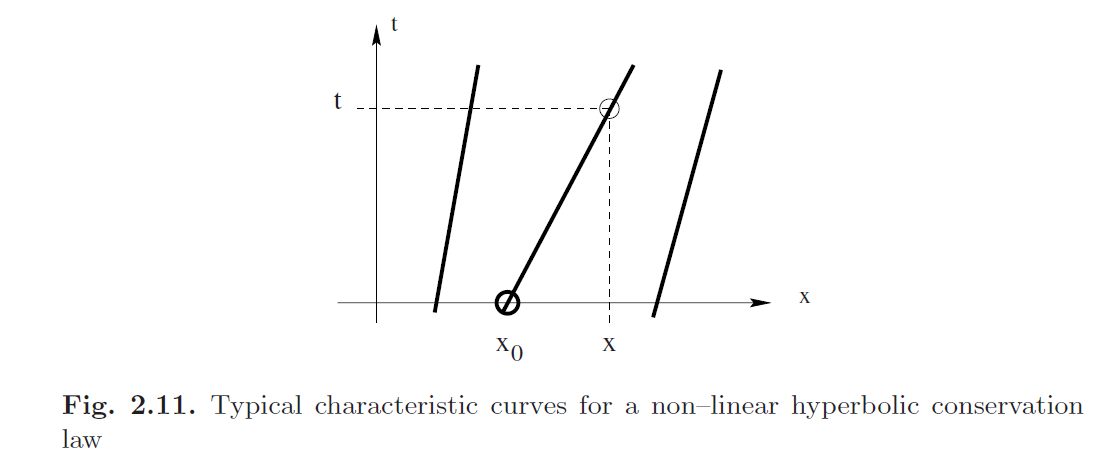
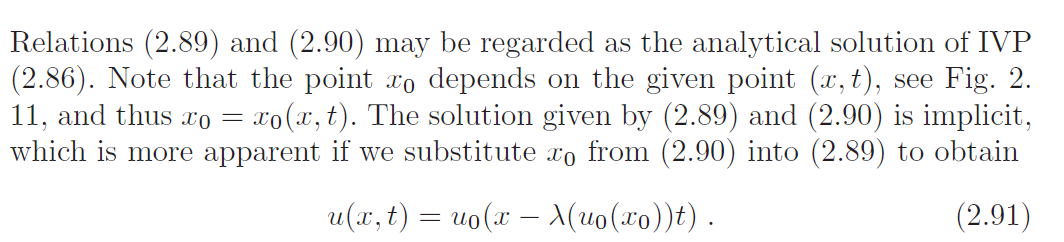
波变陡

回想一下，在线性平流方程的情况下，其中特征速度为λ（u）=a=常数，解由以速度a平移而不失真的初始数据u0（x）组成。在非线性情况下，特征速度λ（u）是解本身的函数。因此产生了扭曲；这是非线性问题的一个显著特征。

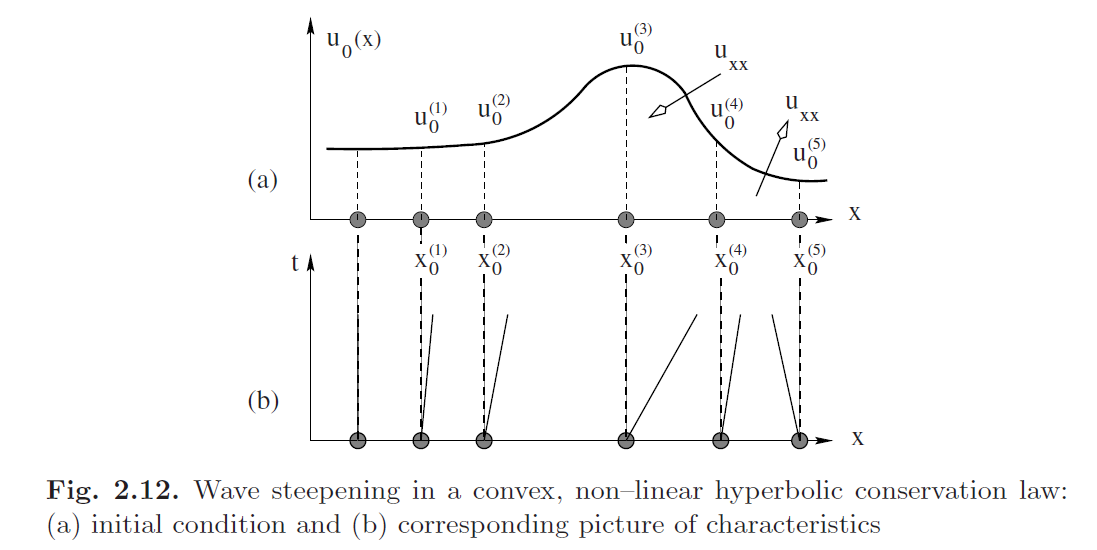
为了解释波失真现象，我们考虑初始数据u0（x），如图2.12所示。平滑的初始轮廓如图2.12a所示，以及五个初始点x（i）0和它们对应的初始数据值u（i）0=u0（x（i）0）。现在让我们假设通量函数f（u）是凸的，也就dλ/du=>0。在这种情况下，特征速度是u的递增函数。Fig. 2.12b shows the characteristics x(i)(t) emanating from the initial points x(i) 0 and carrying the constant initial values u(i) 0 along them. 给定通量的假定凸性，u0（x）的较高值将比u0（x）的较低值传播得更快。There are two intervals on the x–axis where distortions are most evident. These are the intervals IE = [x(1) 0 , x(3) 0 ] and IC = [x(3) 0 , x(5) 0 ]. 在IE中，值u（3）0将比u（2）0传播得更快，并且这反过来又将比u（1）0传播更快。图2.12b中各个特征线的方向清楚地表明了这种情况。
稍后，IE中的初始数据将被转换为更宽和更平坦的轮廓。我们说IE是一个广阔的地区。在膨胀区域，特征速度随着x的增加而增加，即λx>0。相反，区间IC是压缩的，λx<0；值u（3）0的传播速度将快于u（4）0，这反过来又将比u（5）0传播速度快，如图2.12b中各个特征线的方向所示。随着时间的推移，压缩区域往往会变得更陡、更窄。

波浪变陡机制最终将产生解线的折叠，具有相应的特征线交叉和三值解。注意，刚才描述的数据的压缩和膨胀特性与凹通量的情况相反。

激波

空气中的冲击波是压力、密度和温度等物理量变化非常快的小过渡层。强冲击的过渡层与分子的平均自由程具有相同的数量级，约为10−7 m。因此，将这些波替换为数学不连续性是一个合理的近似值。非常微弱的冲击波，如音爆，是一个例外。不连续的近似在一些情况下可能是很不精确的。
回忆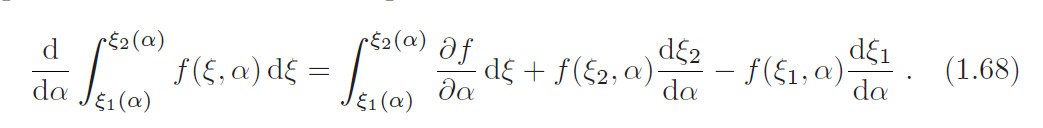

因此，为了允许不连续的解，我们可以根据在解的光滑部分有效的偏微分方程和不连续的Rankine–Hugoniot条件来公式化问题。

不连续解的两个例子

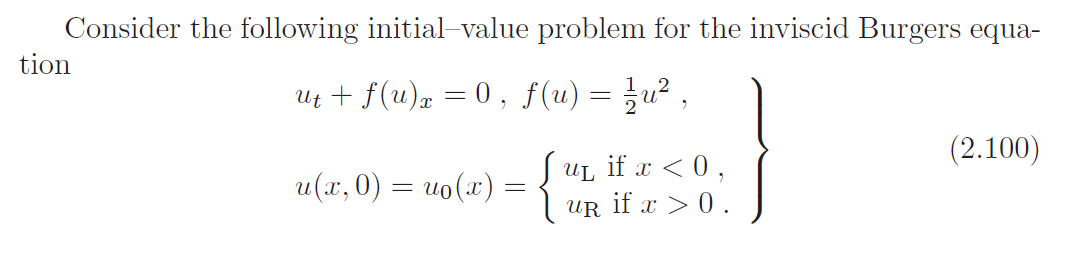
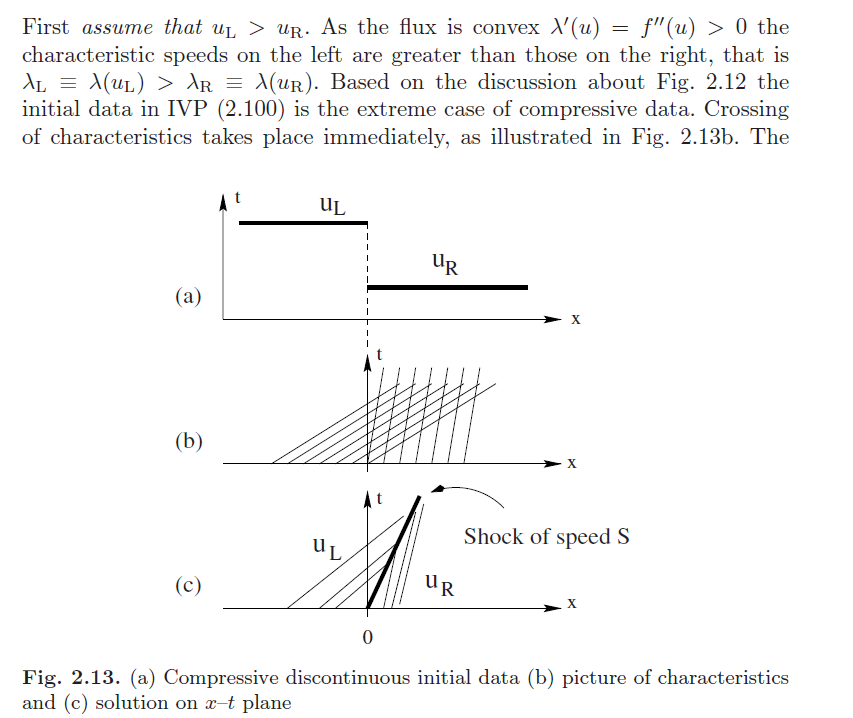
现在我们假设在IVP（2.100）中uL<uR。这个数据是膨胀数据的极端情况，对于凸f（u）。可能的数学解与压缩数据情况下的解（2.101）-（2.102）具有相同的形式
但是，这种解决方案在物理上是不正确的。不连续性不是由于压缩而产生的，λL<λR；特征偏离了不连续性。这个解被称为稀疏激波，或熵破坏激波，并且不满足熵条件（2.103）；因此它被拒绝作为物理解决方案。
比较图2.13和2.14；在压缩的情况下，特征线进入不连续性。考虑到数据的膨胀性，并基于图2.12的讨论，更合理的做法是期望初始数据立即破碎并随着时间的推移而扩展。

膨胀波

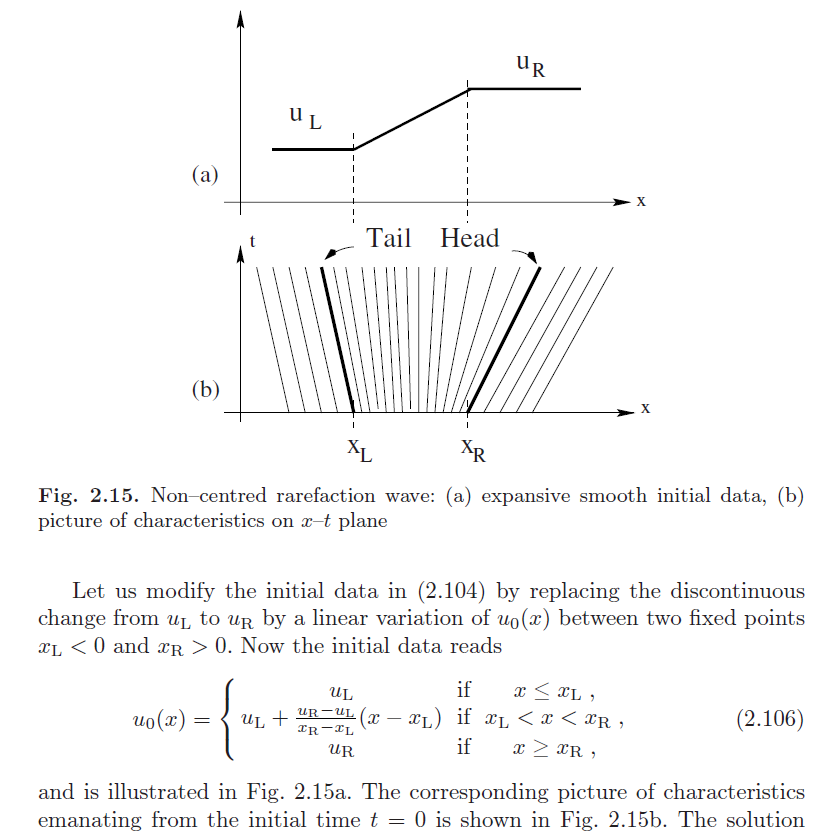
如前所述，该问题的解u（x，t）由以下特征找到，由两个常态uL和uR组成，这两个常状态被数据值uL和u R之间的平滑过渡区域分隔开。这被称为稀疏波。波的右边缘由xR发出的特性给出

无论IVP（2.104）中不连续数据分布的区间的大小Δx=xR−xL有多小，上述膨胀波解的结构都保持不变，与膨胀激波（2.105）完全不同，因为数据的微小变化会导致解的巨大变化。因此膨胀激波解是不稳定的。
根据上述构造，稀疏波解是稳定的，并且当xL和xR分别从下方和上方接近零时，再现IVP（2.104）中x=0处的不连续数据。
因此，极限情况被解释如下：u0（x）在x=0时取uL和uR之间的所有值，因此λ（u0（x））在x=0时取λL和λR之间的全部值。由于较高的值比较低的值传播得更快，初始数据会立即分解，从而产生稀疏波解。这种波的所有特征线都来自一个点的极限稀疏波被称为中心稀疏波。

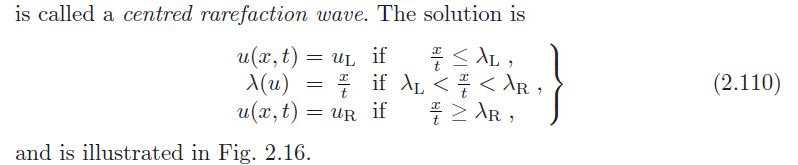
现在我们至少有两个IVP（2.104）的解。因此，在将解的概念扩展到包括不连续性之后，额外的伪解现在是这个扩展类型解的一部分。问题是如何区分物理上正确的解和虚假的解。预期的答案是，除了Rankine–Hugoniot条件（2.98）外，物理不连续性还满足熵条件（2.103）。