PCA自我初步理解
首先PCA的算法很简单,直接从其他地方copy如下:

看到这个,流程上说,就是先均值化,然后求协方差矩阵,对协方差矩阵求特征值和特征向量,按特征值从大到小排列。得出n*k的特征向量矩阵W,再计算XW。就完成了降维。
如何去理解呢?
一般是分为两种理解方法:1.最大方差理论,和最小平方误差理论。
首先,我们首先观察协方差的表示。
样本方差:![]()
样本X和Y的协方差矩阵:
协方差求出来的是一个值,而协方差矩阵求出来的是一个矩阵。
协方差是分布的一个总体参数,是一个统计量。对于多维随机变量\(X=\left[X_1,X_2,...,X_n\right]^T\),计算各维度两两之间的协方差,这样各协方差就组成了一个n*n的矩阵。对角线上的元素是各维度上随机变量的方差。定义协方差矩阵为\(\varSigma\),则里面的每个元素就等于\(\Sigma_{ij}=\operatorname{cov}(X_i,X_j)=\operatorname{E}\big[(X_i-\operatorname{E}[X_i])(X_j-\operatorname{E}[X_j])\big]\)。
即得
\(\Sigma=\begin{bmatrix} \operatorname{cov}(X_1, X_1) & \operatorname{cov}(X_1, X_2) & \cdots & \operatorname{cov}(X_1, X_n) \\ \operatorname{cov}(X_2, X_1) & \operatorname{cov}(X_2, X_2) & \cdots & \operatorname{cov}(X_2, X_n) \\ \vdots & \vdots & \ddots & \vdots \\ \operatorname{cov}(X_n, X_1) & \operatorname{cov}(X_n, X_2) & \cdots & \operatorname{cov}(X_n, X_n) \end{bmatrix}.\)
那下一步,对于三维数据(x,y,z),则有
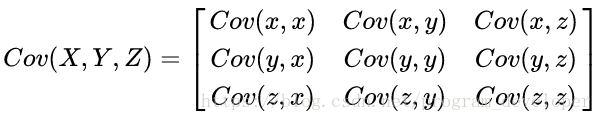
对m维数据,就是
$$
cov\left( X_1,X_2,...,X_m \right) =\left[ \begin{matrix}
cov\left( X_1,X_1 \right)& cov\left( X_1,X_2 \right)& ...& cov\left( X_1,X_m \right)\\
cov\left( X_2,X_1 \right)& cov\left( X_2,X_2 \right)& ...& cov\left( X_2,X_m \right)\\
...& ...& ...& ...\\
cov\left( X_m,X_1 \right)& cov\left( X_m,X_2 \right)& ...& cov\left( X_m,X_m \right)\\
\end{matrix} \right]
$$。
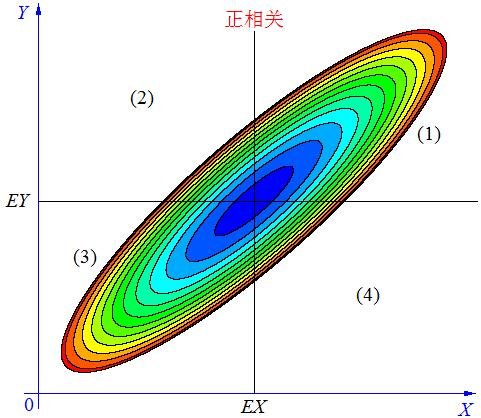
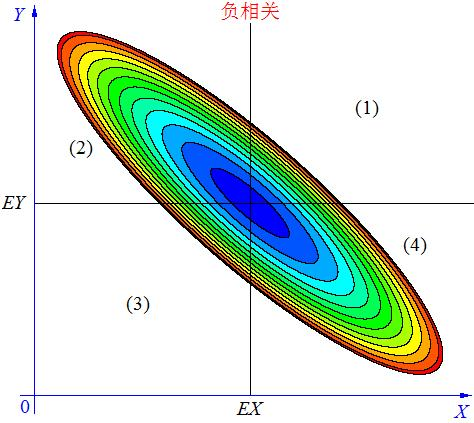
我们看协方差cov,可以看到,对任意两个随机变量 \(x\)和\(y\),\(cov\left(x,y\right)=E\left(x-\overline{x}\right) \left(y-\overline{y}\right)\),也就是看x偏离均值的程度与y偏离均值的程度的相关程度,当cov大于0,正相关。小于0,负相关,等于0,不相关。
我们接下来用的协方差矩阵是计算样本不同维度之间的协方差,而不是对不同样本计算,所以协方差矩阵的大小与维度相同。协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。为什么用这个,就是我们希望找到一个矩阵P,可以将这个协方差矩阵变成对角阵,也就是,使得不同多维随机变量之间不存在相关性,不存在相关性,则信息冗余就减少了。也就是\(cov\left(x,y\right)=0, where x \ne y, cov\left(x,y\right) \ne 0, where x=y\)。
现在我们要做的就是将协方差矩阵对角化:即除对角线外的其他元素化为0,并且在对角线上将元素按大小从上到下排列。如此,就是找一个P,P是n*k矩阵,使得C是一个从上到下从大到小排列的对角阵。要这样做的目的,是希望尽可能的减少冗余性,也就是减少成分之间的相关性。如何做到这一点呢,就是希望成分之间尽可能的正交。那么具体如何处理呢?就是从原始的空间中,顺序的找出一组相互正交的坐标轴,先找第一个,找完后再找第二个,第二个要和第一个正交;第三个要和第一个,第二个正交。以此类推去得到。就是希望能量尽可能的不产生关联。
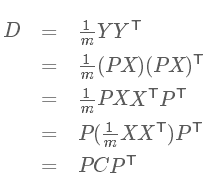
1.最大投影方差理论
也就是构建一个新的坐标系,一个个的确定方向,使得,原始数据点投影到新的坐标系方向后,到原点(均值)的方差达到最大。 先找一个方向,使得投影到新的方向时,所有投影点离原点的距离平方和最大;方差最大,也就是能量最大,把尽可能多的能量方向找到(也就是变化),然后依次找,这样,将尽可能多的能量聚集在前K个维度,从而达到降维的目的。
\(\frac{1}{m}\sum_{i=1}^m (x^{(i)T}w)^2 = \frac{1}{m}\sum_{i=1}^m w^T x^{(i)} x^{(i)T}w =\sum_{i=1}^m w^T (\frac{1}{m} x^{(i)} x^{(i)T})w_1\)
2.最小平方误差理论
其实想法也很简单,就是一个三角理论,数据点到原点的距离,是固定的,也就是三角形的斜边确定了,那么如果投影点到原点的距离要去越大,那么投影点到数据点的距离就会越小,\(z^2=x^2+y^2\),应该就是这么简单。也就是最小化降维所造成的能量损失。也就是新的坐标方向,使得原协方差矩阵对角化,同时使得能量损失最少。
\(\sum_{i=1}^{m}(x^{(i)’} - x^{(i)})^2\)
但是不同的是,在欧式空间中这两种理论是等价的,但是如果在流形中,空间会存在扭曲和密集程度不同等等问题,主成分方向不一定是直线了,均值点的定义也会改变了,可能两种理论就不等价了,就需要新的解释。
PCA算法优缺点:
优点:
1.无监督学习,没有参数限制。
2,数据压缩降维。
3.各主成分之间相互正交,减少互相影响和冗余。
4.方法易于实现。
缺点:
1.贡献小的主成分可能对样本内部的差异性有重要作用;
2.对数据的一些先验的知识,因为没有参数,就无法用参数化等方法对处理过程进行干预和支持。
其他的自己也不太了解,敬请大家指正。

