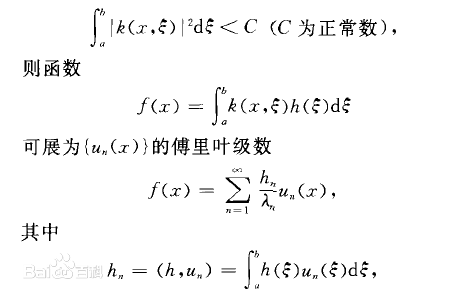流形上的函数型数据表示

令M 是一个内在维度为d的函数型流形，$\psi$是M的一个表示映射。则定义$X \in \mathcal{M}$， ，且是双射，$\psi$与$\varphi$是互逆，都连续。

 

$\mu$ 是d维表示空间的均值。$\mu^{\mathbb{M}}$是$L^2$空间的流形平均。其实就是本来流形M是在一个L2空间中，$\psi$将x映射到欧式$R^d$中，得到均值$\mu$，然后再倒回去，$\mu^{\mathcal{M}}$就是$L^2$空间上的均值。

如果M是等距的，则$\mu^{\mathcal{M}}$就是唯一的，对所有的等距映射来说，则$\mu^{\mathcal{M}}$有了新的表示：

                                                                               

其中，$d_g$ 表示测地距离（geodesic distance）。

考虑random functions $X\in L^2\left( \mathcal{T} \right)$，$\mathcal{T}$ 是有界区域。$\mu\left( t \right)=EX \left( t \right)$ 以及 $G \left( t,s \right) =Cov \left( X \left( t \right) , X\left( s \right) \right)$ 。由mercer定理，如果G是联合连续的，那么G就有有一个由特征值和特征向量组成的标准正交展开：

                                                                       

用Hilbert-Schmidt 定理，X可以由KL展开表示，即

                                                     

$\xi_k$是不相关的随机向量with均值为0，方差为$\lambda_k$，即函数型主成分。这里的主成分都在d维流形上。

因此X用基于特征方程的表示可以是

                                              

其中，$\lambda_j^{1/2}$ 令所有j的尺度保持统一标准，函数在特征函数$\phi_j$方向上的变化可以由$\alpha$改变看到。

而当functional data 在一个manifold上时，linear modes 很难表现数据的敏感的变化。

因此定义了函数型流形成分functional manifold component(FMC) vectors $e_j$ in$\mathbb{R}^d$，j=1,...,d. 

$e_j$是 $\psi \left( X \right) \in \mathbb{R}^d$  的协方差矩阵的特征向量，即，其中，是cov($\psi$(X))的特征值。首先要明白，我们是要将L2上的数据先投影到$\mathbb{R}^d$上，再去求协方差。因此也容易知道$\e_j$肯定是$\mathbb{R}^d$上的。

则，用流形模式表示函数型变化即：

                                             

$\mu$是d维表示上的均值，很好理解。而$\phi_{-1}$是从d维到M上的映射，也就是，$\phi^{-1}\mu$就是$\mu_\mathcal{M}$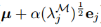，就是d维空间的$X_{j,a}$的表示。

而且此$X_{j,a}^\mathcal{M}$对于isometric的M，是唯一确定的，有定理可证。

 

因此，对于任何$X\in \mathcal{M}$，给定$\phi$，X能被向量$\mathcal{v}=(\mathcal{v_1},...,\mathcal{v_d}) \in \mathbb{R}^d$唯一表出。

                                                     

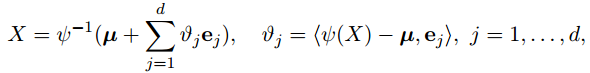
其中，内积是$\mathbb{R}^d$上的内积，$\mathcal{v}$是不相关的r.v.s(随机变量序列)with mean=0 & variance $\lambda_j^\mathcal{M}$。则 $\mathcal{v}$就是函数型流形成分(FMCs)。

参考文献：nonlinear manifold representations for functional data(2012)

 附：Hilbert-Schmidt 定理