数论（一）

一.质数

1.试除法判断素数：

#include<bits/stdc++.h>
using namespace std;
bool is_prime(int n)
{
    if(n<2)
    return false;
    for(int i=2;i<=n/i;i++){  //如果用sqrt(n)，每次执行都要开方会导致耗费时间，如果是i*i，再进行++有可能导致溢出。
         if(n%i==0)
            return false;
     }
      return true;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        if(is_prime(n))
        printf("Yes\n");
        else
        printf("No\n");
        
    }
}

时间复杂度o（sqrt（n））

2.分解质因数试除法：

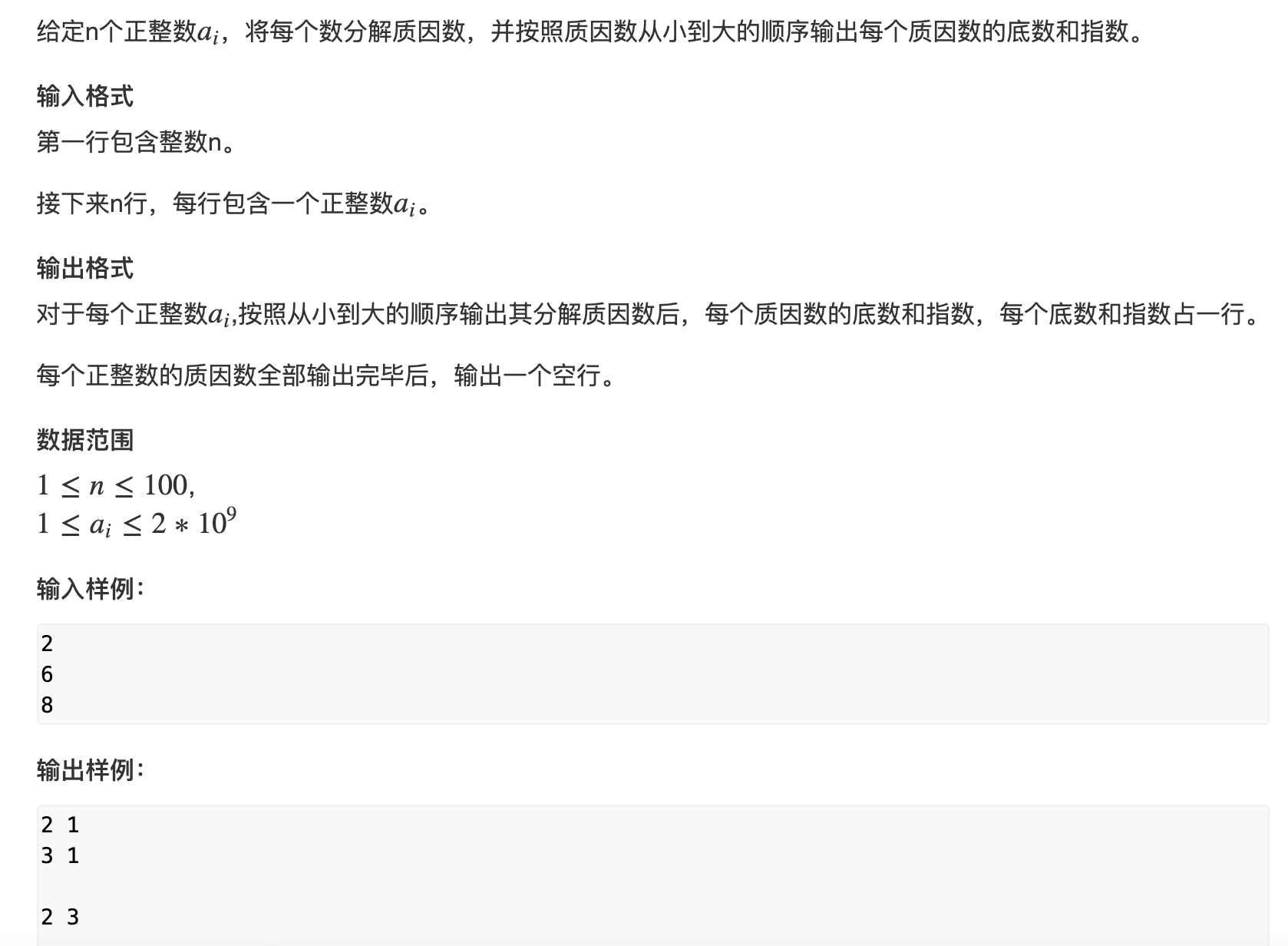
#include<bits/stdc++.h>
using namespace std;
void divide(int n)
{
    for(int i=2;i<=n/i;i++){
        if(n%i==0)
        {
            int s=0;
            while(n%i==0)
            {
                n/=i;
                s++;
            }
            printf("%d %d\n",i,s);
        }
        
    }
    if(n>1) printf("%d %d\n",n,1);  //处理大于sqrt(n)的质数因子
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        divide(n);
        printf("\n");
    }
}

时间复杂度：logn～sqrt（n）

3.筛法判断质数：

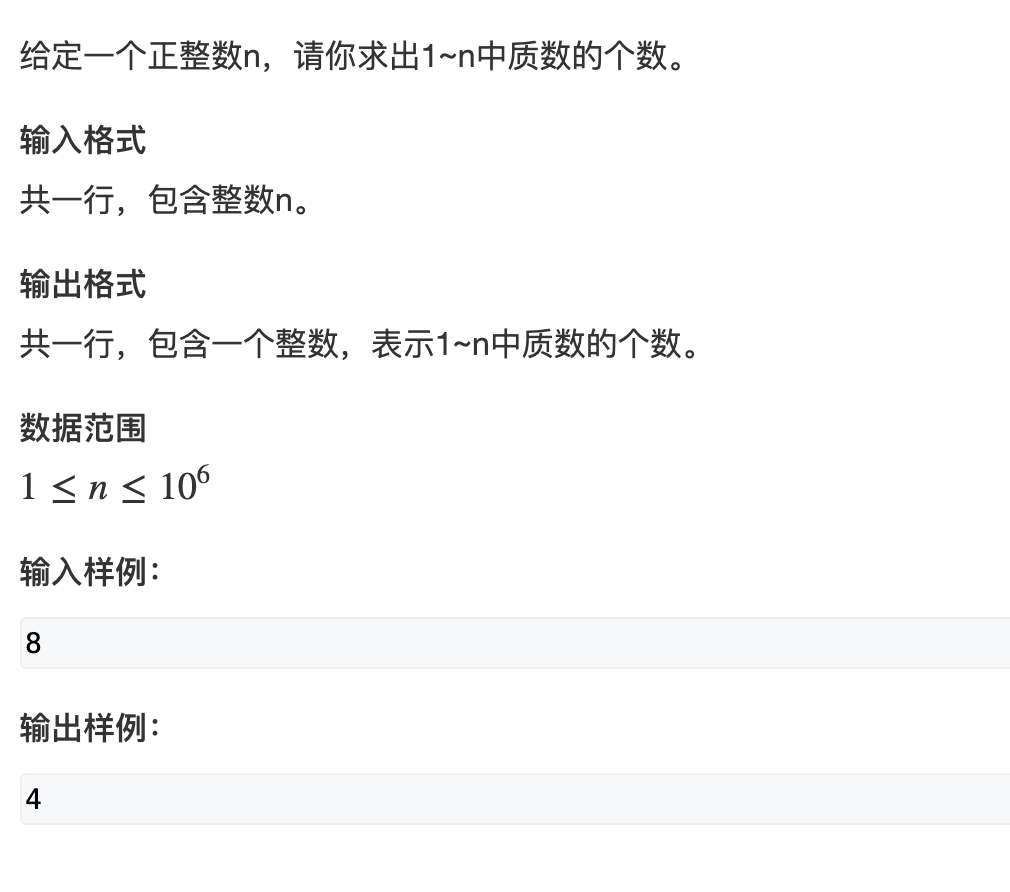
埃氏筛法：

#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
bool sti[N];
int cnt;
int prime[N];
int is_prime(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!sti[i])
        {
            prime[cnt++]=n;
            for(int j=i+i;j<=n;j+=i)
            sti[j]=true;
        }
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    is_prime(n);
    printf("%d\n",cnt);
    
}

线性筛法：

#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
bool sti[N];
int cnt;
int prime[N];
int is_prime(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!sti[i]) prime[cnt++]=i;
        for(int j=0;prime[j]<=n/i;j++)    //在1～n区间里筛掉合数
        {
            sti[i*prime[j]]=true;
            if(i%prime[j]==0) break;   //不是最小质因数，就直接跳出循环，防止循环冗余
        }
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    is_prime(n);
    printf("%d\n",cnt);
    
}