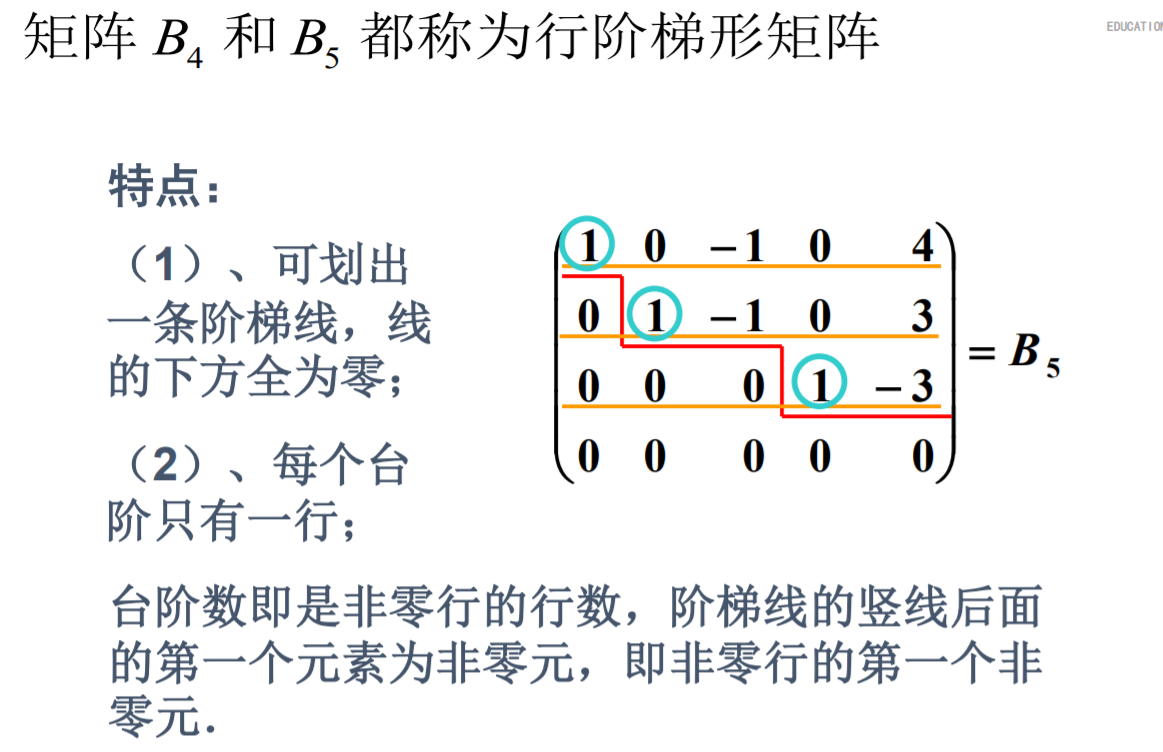
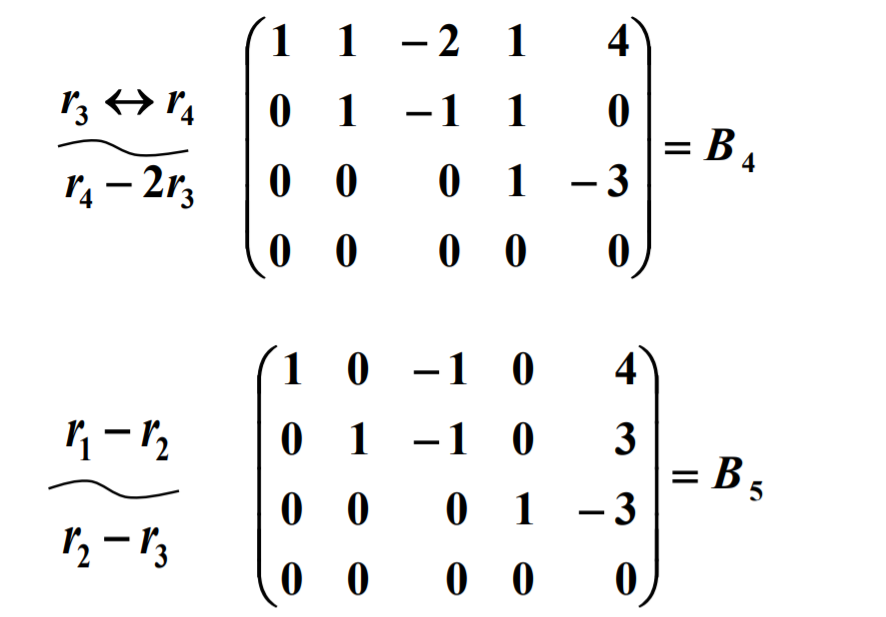矩阵的初等变换

矩阵变换是线性代数中矩阵的一种运算形式。

在线性代数中，矩阵的初等变换是指以下三种变换类型 ：

(1) 交换矩阵的两行（对调i,j，两行记为ri，rj）；

(2) 以一个非零数k乘矩阵的某一行所有元素（第i行乘以k记为ri×k）；

(3) 把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素(第j行乘以k加到第i行记为ri+krj)。

类似地，把以上的“行”改为“列”便得到矩阵初等变换的定义，把对应的记号“r”换为“c”。

矩阵的初等行变换与初等列变换合称为矩阵的初等变换（来源百度百科）

矩阵的初等变换（矩阵不变）

行阶梯形矩阵

行最简形