剑指Offer | 搜索与回溯算法

剑指 Offer 12. 矩阵中的路径

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 "ABCCED"（单词中的字母已标出）。

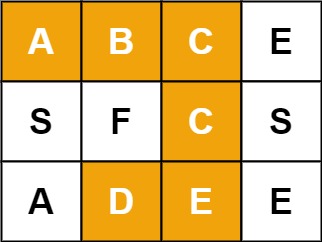
示例 ：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

提示：

• 1 <= board.length <= 200
• 1 <= board[i].length <= 200
• board 和 word 仅由大小写英文字母组成

方法：深度搜索+剪枝

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        // 此处的 row 和 col 是this 指针下的成员，前面一定不可以加int
        row = board.size();
        col = board[0].size();

        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                // 如果以当前节点作为单词头能找到匹配的路径，则返回true
                if(dfs(board, word, i, j, 0)) return true;
            }
        }
        return false;
    }
private:    
    int row, col;
    bool dfs(vector<vector<char>>& board, string word, int i, int j, int k) {
        // 判断越界和不符的情况
        if(i>=row || i<0 || j>=col || j<0 || board[i][j]!=word[k])return false;
        if(k == word.size()-1) return true;
        // 跳出了第一句判断，说明两边的字符相匹配，因此将该值暂时赋值'\0'，方便后面匹配
        board[i][j] = '\0';
        bool res = dfs(board, word, i+1, j, k+1) || dfs(board, word, i-1, j, k+1) || dfs(board, word, i, j-1, k+1) || dfs(board, word, i, j+1, k+1);
        // 还原之前被置为'\0'的字符，被置为'\0'一定是因为字符相匹配，所以还原时也可以直接赋值
        board[i][j] = word[k];
        return res;
    }
};

参考：

K神写的就是清晰易懂

剑指 Offer 13. 机器人的运动范围

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 ：

输入：m = 2, n = 3, k = 1
输出：3

提示：

• 1 <= n,m <= 100
• 0 <= k <= 20

方法：深度搜索

class Solution {
public:
    int movingCount(int m, int n, int k) {
        // 创建辅助数组 visited
        vector<vector<bool>> visited(m, vector<bool>(n, 0));
        return dfs(visited, m, n, 0, 0, k);
    }

    int dfs(vector<vector<bool>>& visited, int m, int n, int i, int j, int k) {
        // 遇到非法情况，返回0
        if(i>=m|| j>=n || !isLegal(i, j, k) || visited[i][j]) return 0;
        // 否则选中，将该位置的 visited 置为 true
        visited[i][j] = true;
        // 然后往下和往右遍历
        return 1 + dfs(visited, m, n, i+1, j, k) + dfs(visited, m, n, i, j+1, k);
    }
    // 行列之和与k比较，判断合法性
    bool isLegal(int i, int j, int k) {
        int sum = 0;
        while(i != 0) {
            sum += i % 10;
            i /= 10;
        }
        while(j != 0) {
            sum += j % 10;
            j /= 10;
        }
        return (sum > k) ? false : true;
    }
};