通过 n 进制整数对称加法,寻找回文串数字
一、题目描述
- 若一个数(首位不为零)从左向右读与从石向左读都一样,我们就将其称之为回文数。
- 例如:给定一个十进制数 56,将56加65(即把56从右向左读),得到 121 是一个回文数。
- 又如:对于十进制数 87:
- STEP1: 87 + 78 = 165
- STEP2: 165 + 561 = 726
- STEP3: 726 + 627 = 1353
- STEP4: 1353 + 3531 = 4884
- 又如:对于十进制数 87:
- 在这里的一步是指进行了一次 N 进制的加法,上例最少用了 4步得到回文数 4884。
- 写一个程序,给定一个 N (2≤N≤10或N=16) 进制数 M (100位之内),求最少经过几步可以得到回文数。如果在30 步以内(包含 30步)不可能得到回文数,则输出 Impossible!
输入格式
- 两行,分别是N,M.
输出格式
- Impossible! 或者 步骤数 K
二、 解题思路:
这道题可以分解为两个小问题:
- 一个 n 进制的数 m 的对称的加法运算。 可以定义为一个函数 add_n(n, m). 其中 n 为进制, m 为该进制下的一个数。
- 判断一个数 sum 是不是 回文数。按照回文的定义,定义一个 bool 返回值函数 isPalindrome(sum).
PS: 第一个问题包含一个子问题: 即判断一下输入的数 m 是不是 有效的 n 进制数。 isValid(n, m)
三、代码
- 函数:
isPalindrome(sum)判断sum是否是回文串。
def isPalindrome(sum):
''' 该函数:判断整数 sum 是不是回文,返回 True 或 False'''
return (int(str(sum)[::-1]) == sum)
- 函数
add_n(n, m)将 将 n进制的 整数m 与其 反串 mk 相加(满足 n 进制相加运算),返回一个 n 进制的 整数和。
def add_n(n, m):
''' 该函数将 n进制的 整数m 与其 反串 mk 相加(满足 n 进制相加运算),返回一个 n 进制的 整数和'''
ms = str(m) # 将 整数转化为 字符串 ms
mk = ms[::-1] # 将 ms 翻转 为mk , 比如: 87 反转 为 78
sum = ""
ll = 0
# 特别注意: 这里是从左边向右边 进行➕ 运算的。与一般的加法不一样的,是 反次序的。
# 一般情况下不可以,但是这里 ms 和 mk对称的,所以不影响结果,最后sum 只需要 反过来一下。
for i in range(len(ms)):
temp = int(ms[i]) + int(mk[i]) +ll
kk, ll = temp % n, temp // n # kk ,ll 分别为余数和商
sum += str(kk)
if ll > 0 : sum +=str(ll) # 确保 最右边 进位 要被加上去。
return(int(sum[::-1]))
- 函数
isValid(n, m)判断 整数m 是否满足 有效n 进制的表示,即 m 中的最大数字应该小于 n '''
def isValid(n, m):
''' 该函数:判断 整数m 是否满足 有效n 进制的表示,即 m 中的最大数字应该小于 n '''
result = True
for c in str(m):
if int(c) >= n:
result = False
break
return result
- 主程序:接受两个输入,“N, M”,输出需要进行的加法步骤 和 最终的 回文串
# main
N = int(input("输入一个n进制(2<= n <=10 或 n = 16):"))
M = int(input("输入一个n进制的数:"))
if not isValid(N, M): # 检查有效性
print("数 {} 不是有效的 {} 进制数".format(M, N))
else:
sum = M
for step in range(1, 30):
sum = add_n(N, sum)
if isPalindrome(sum):
print("after {} steps add, we obtain {}".format(step, sum))
break
else:
print("Impossible!")
- 改进版1:将中间过程打印出来
# main
N = int(input("输入一个n进制(2<= n <=10 或 n = 16):"))
M = int(input("输入一个n进制的数:"))
if not isValid(N, M): # 检查有效性
print("数 {} 不是有效的 {} 进制数".format(M, N))
else:
sum = M
for step in range(1, 30):
sum = add_n(N, sum)
if isPalindrome(sum):
print("after {} steps add, we obtain {}".format(step, sum))
break
else:
print("STEP {}: {} + {} = {} ".format(step, M, int(str(M)[::-1]), sum))
M = sum # M 换成这一轮的结果 sum。 下一轮循环,将执行 n进制 整数sum的加法操作
else:
print("Impossible!")
- 执行测试1: 结果OK

- 执行测试2: 结果出错! 不打印第一步!

- 改进版 2 :消除 改进版1 的bug
# main
N = int(input("输入一个n进制(2<= n <=10 或 n = 16):"))
M = int(input("输入一个n进制的数:"))
if not isValid(N, M): # 检查有效性
print("数 {} 不是有效的 {} 进制数".format(M, N))
else:
sum = M
for step in range(1, 30):
sum = add_n(N, sum)
print("STEP {}: {} + {} = {} ".format(step, M, int(str(M)[::-1]), sum))
if isPalindrome(sum):
print("After {} steps add, we obtain {}".format(step, sum))
break
else:
M = sum # M 换成这一轮的结果 sum。 下一轮循环,将执行 n进制 整数sum的加法操作
else:
print("Impossible!")
-
执行测试1: 结果OK

-
执行测试2: 结果OK

四、 编程时发现的一个Python程序设计语言的缺陷
IndexError: Replacement index 3 out of range for positional args tuple
- 在上述代码 4 部分:
- 正确语句:
print("STEP {}: {} + {} = {} ".format(step, M, int(str(M)[::-1]), sum))注意format()的 括号配对 - 错误语句:
print("STEP {}: {} + {} = {} ".format(step, M, int(str(M)[::-1])), sum)注意format()的 括号配对出错了,但是编译时候并不能发现,只能在运行时候报错。
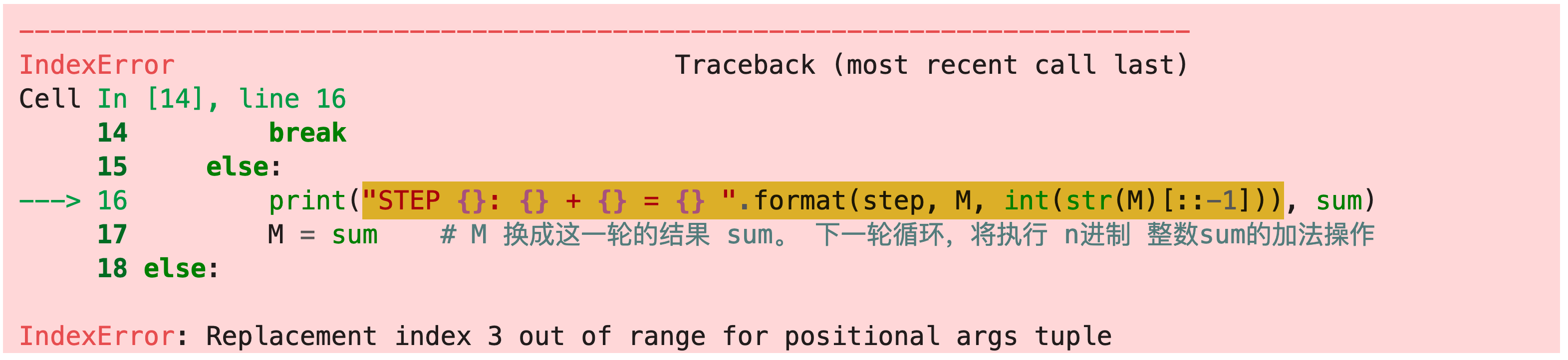
- 正确语句:
思考: 为什么实际定义时候,发现不了呢! 非要等运行时候 才会报错?
- "IndexError: Replacement index 3 out of range for positional args tuple"
五、 利用大模型进行代码审查
-
Gemini 返回结果
程序中植入错误语句:print("STEP {}: {} + {} = {} ".format(step, M, int(str(M)[::-1])), sum)Prompt 如下:
N = int(input("输入一个n进制(2<= n <=10 或 n = 16):")) M = int(input("输入一个n进制的数:")) if not isValid(N, M): # 检查有效性 print("数 {} 不是有效的 {} 进制数".format(M, N)) else: sum = M for step in range(1, 30): sum = add_n(N, sum) if isPalindrome(sum): print("after {} steps add, we obtain {}".format(step, sum)) break else: print("STEP {}: {} + {} = {} ".format(step, M, int(str(M)[::-1])), sum) M = sum # M 换成这一轮的结果 sum。 下一轮循环,将执行 n进制 整数sum的加法操作 else: print("Impossible!")Gemini 输出如下:
5.1 代码分析:
该代码旨在检查一个给定的n进制数是否可以通过重复n进制整数加法操作变成回文数。
以下是可能出错的语句及其原因:
-
isValid(N, M)函数未定义:代码中使用了
isValid(N, M)函数来检查输入的n进制数是否有效,但该函数未在代码中定义。这会导致运行时错误,因为程序会尝试调用一个不存在的函数。解决方案:定义
isValid(N, M)函数,该函数应检查n进制数是否在规定的范围内(2 <= n <= 10 或 n = 16)并且每个数字都是有效的n进制数字。 -
循环终止条件可能有问题:
内部循环使用
for step in range(1, 30)进行迭代,这限制了最大可能的步骤数为30。如果输入的n进制数需要更大步骤数才能变成回文数,那么循环将提前终止,导致错误结果。解决方案:考虑使用
while循环代替for循环,并使用更合适的终止条件,例如判断sum是否等于回文数或达到最大可能的步骤数。 -
字符串格式化错误:
在
print("STEP {}: {} + {} = {} ".format(step, M, int(str(M)[::-1])), sum)语句中,使用了int(str(M)[::-1])来获取M的逆序表示。然而,对于n进制数大于10的情况,直接将字符串转换为整数可能会丢失精度,导致错误结果。解决方案:对于n进制数大于10,应使用n进制表示进行逆序和加法操作,而不是将其转换为十进制表示。
-
加法函数
add_n未定义:代码使用了
add_n(N, sum)函数来执行n进制整数的加法操作,但该函数未在代码中定义。这会导致运行时错误,因为程序会尝试调用一个不存在的函数。解决方案:定义
add_n(N, sum)函数,该函数应实现两个n进制整数的加法操作,并返回结果。n进制加法需要考虑进位情况,可以使用类似于十进制加法的方法进行实现。
5.2 建议:
- 完善代码,定义缺失的函数
isValid(N, M)和add_n(N, sum)。 - 调整循环终止条件,避免因最大步骤数限制导致错误。
- 修复字符串格式化问题,对于n进制数大于10,使用n进制表示进行逆序和加法操作。
- 仔细检查代码逻辑,确保没有其他潜在的错误或遗漏。
5.3 额外说明:
- 建议使用更具描述性的变量名,例如将
N改为base,将M改为number,使代码更易读。 - 可以添加更多的错误处理机制,例如当输入无效或达到最大步骤数时,程序能够提供更清晰的提示信息。
六、根据LLM 代码分析提示,优化后的代码
6.1 优化后,定义成4个函数
# 优化后的 4 函数定义
# 函数1
def isPalindrome(number):
''' 该函数: 判断整数 number 是不是回文
输 入: 一个整数 number (是 base进制的,2≤ base ≤10或 base=16)
输 出: True 或 False (是否为回文!)
'''
return (int(str(number)[::-1]) == number)
# 函数2
def isValid(number, base = 10):
''' 该函数:判断 整数 number 是否满足 有效 base进制的表示,即最大数字应该小于 base
输 入:一个整数 number , number是 base进制的
一个整数 base, 缺省值为10, 2≤ base ≤10或 base=16
输 出: True 或 False (number是否为有效base进制数!)
'''
valid = True
for c in str(number):
if int(c) >= base:
valid = False
break
return valid
# 函数3
def add_n(number, base = 10):
''' 该函数将 base 进制的 整数 number 与其 反串 number_sk相加(满足 base 进制相加运算)
返回一个base进制的整数和串(sum_s)
输入: 一个 base 进制的 整数 number
base, 指定加法操作遵循的进制
输出:加法操作的结果,整数和串(sum_s)对应的整数
'''
number_s = str(number) # 将 整数转化为 字符串 number_s
number_sk = number_s[::-1] # 将 number_s 翻转 为 number_sk, 比如: 87 反转 为 78
sum_s = "" # sum_s 用于存放 base进制的整数和串(sum_s 是字符串)
quotient = 0 # base进制两个数字相加时,用作进位值
# 特别注意: 与一般的加法从右向左加不一样的,这里是从左向右进行加运算(反次序)的。
# 一般情况下不可以,但是这里 number_s和 number_sk对称的,所以不影响结果,最后sum_s 只需要 反过来一下。
for i in range(len(number_s)):
temp = int(number_s[i]) + int(number_sk[i]) + quotient
# remainder, quotient 分别为相加的结果 temp 除以base的 余数和 商,其中商要作为进位
remainder, quotient = temp % base, temp // base
sum_s += str(remainder)
# 确保循环结束时候,最右边 不为零的进位 要被加上去。
if quotient > 0 : sum_s +=str(quotient)
return(int(sum_s[::-1]))
# 函数4
def findPalindrome(number, maxSteps = 30, base = 10):
''' 该函数在有限的MaxSteps步骤内,执行 number、number逆序加操作,迭代进行,直到寻找到回文数。
'''
if not isValid(number, base): # 检查有效性
print("数 {} 不是有效的 {} 进制数".format(number, base))
else:
sum = number
for step in range(1, maxSteps):
sum = add_n(sum, base)
print("STEP {}: {} + {} = {} ".format(step, number, int(str(number)[::-1]), sum))
if isPalindrome(sum):
print("After {} steps add, we obtain {}".format(step, sum))
break
else:
number = sum # number 换成这一轮的结果 sum。 下一轮循环,将执行 n进制 整数sum的加法操作
else: # 注意:这里的else 属于 for循环的子句
print("Impossible!")
6.2 测试脚本
-
测试1:
findPalindrome(7)- 结果:
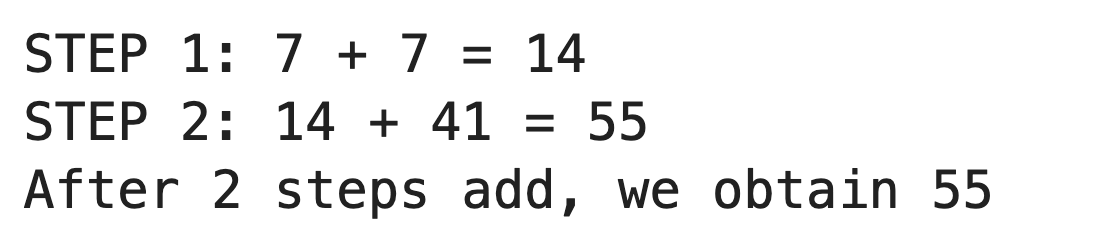
- 结果:
-
测试2:
- 代码:
for i in range(1,100): print("Round {}: Operations as following ................ ".format(i)) findPalindrome(i) print() - 结果:
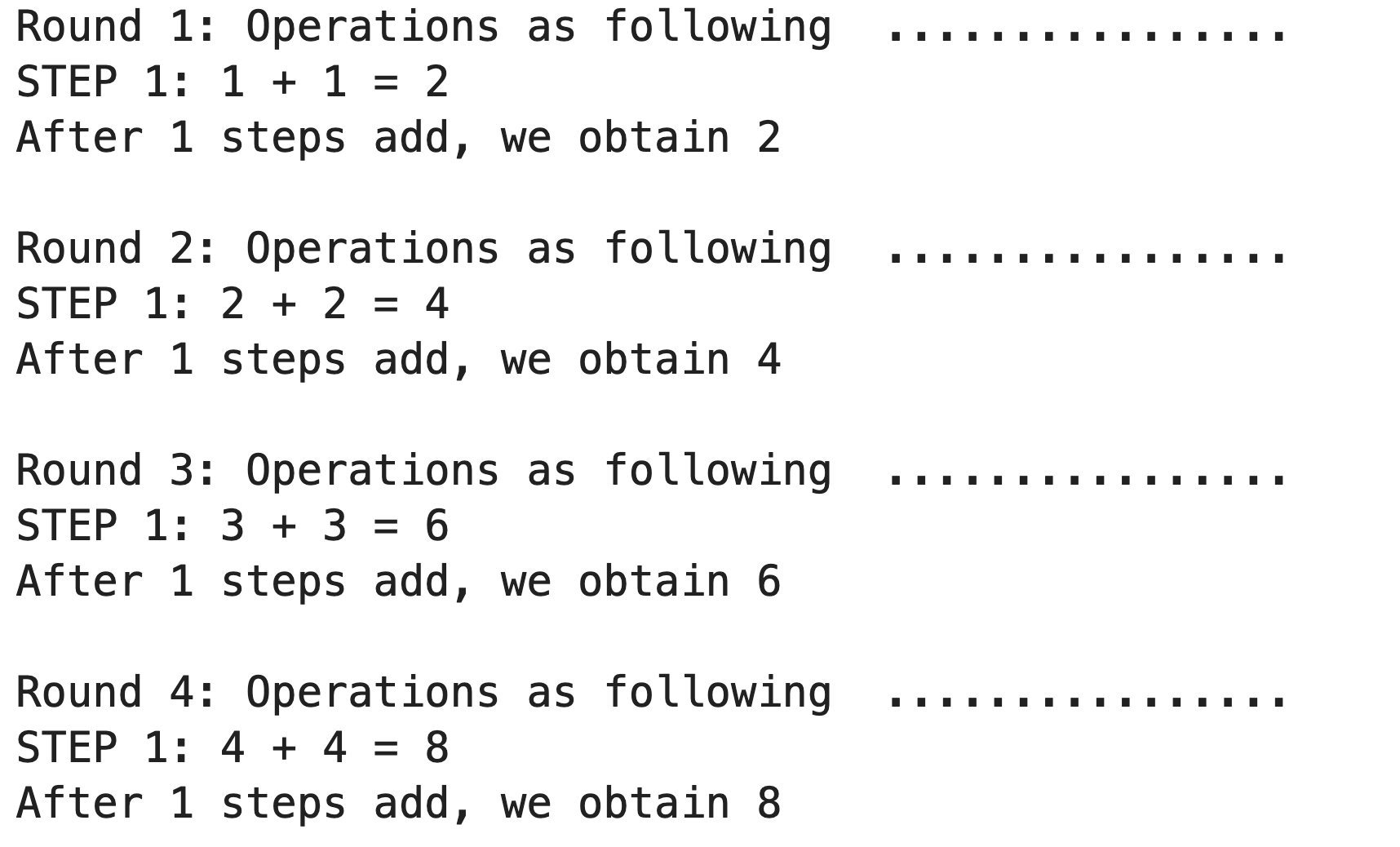
- 代码:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号