正多边形内点黄金分割冒险游戏
1. 题目:
正多边形 内点的冒险游戏
内容描述:
- 选定五边形(P1, P2, ..., P5)内的一个任意点 P0 。
- 从 P0 出发,到任意顶点距离的 0.618 的点P0’(黄金分割点),给该P0’点着色。
- 从P0’点出发,重复第2步, 求得新的黄金分割点并着色。
- 以上重复 N 次,比如,30000次
问题: 最后所有黄金分割点形成的图案。
2. 思考
-
步骤一: 正多边形生成问题
- 以原点为中心,长度为a,每次旋转 angle = 2* PI /n 弧度 .
- 计算顶点的坐标 : Points ( a * cos(angle), angle
- 计算正多边形的顶点坐标集合。 Points(a * cos(angle), a * sin(angle) )
- 上述步骤定义成一个函数,返回一个列表,列表的每一项为坐标(x,y)
-
步骤二:黄金分割点的计算 :P0点到 PN点 距离的 0.618
- P0' = P0 + (PN-P0) * 0.618
-
步骤三:显示多边形和黄金分割点
- 用 plot 或 scatter 画线 和 点
3. 代码
- 步骤一:定义正多边形函数
# Step 1.1 : 定义 正 n 边形的函数,calculate_pentagon_vertices, 返回顶点坐标列表
# 方法,以原点为中心,旋转 angle = 2 * math.pi / n 弧度,然后利用cos,sin 计算顶点坐标
#
import math
def calculate_pentagon_vertices(a, n): # a 为原点到顶点的距离 ,n 为正n 边形顶点个数
# 正 n边形的中心角度
angle = 2 * math.pi / n
# 列表 vertices存放顶点坐标,用于返回
vertices = []
# 计算正n边形的顶点
for i in range(n):
# 计算每个顶点的x和y坐标
x = a * math.cos(i * angle)
y = a * math.sin(i * angle)
vertices.append((x, y))
return vertices
# step 1. 2: 调用函数,得到一个顶点列表 vertices
vertices = calculate_pentagon_vertices(2,5)
- 步骤二:计算黄金分割点,并显示
# step 2: 计算黄金分割点,并显示
import matplotlib.pyplot as plt
import random
Golden = 0.618
Number = 40000 # 黄金分割次数
# vertices 将第1项追加尾部,为了绘图时候首尾相连。注意:执行后vertices长度增加了一个
vertices.append(vertices[0])
X = [Point[0] for Point in vertices] # Point 为顶点
Y = [Point[1] for Point in vertices]
# 使用plot()绘制正多边形
plt.plot(X, Y, marker='o', linestyle='-') # marker='o' 指定点为圆圈,linestyle='-' 指定线为实线
# 单独绘制起始点 ,我们这里设置为原点
plt.plot(0, 0, 'ro') # 'r' 表示红色,'o' 表示圆圈
P0_x, P0_y = 0, 0
plot_x = [] # 方法三:存放所有黄金分割点的 坐标,P0_x
plot_y = [] # 方法三:存放所有黄金分割点的 坐标,P0_y
for i in range(Number):
# 随机指定一个顶点 PN
PN = random.randint(1,len(vertices)-1)
# 求 P0 --- PN 之间的新的点,仍然记为 P0
P0_x = P0_x + (X[PN]- P0_x)* Golden
P0_y = P0_y + (Y[PN]- P0_y)* Golden
# plt.plot(P0_x, P0_y, 'go') # 方法一: plot 绘图 'r' 表示红色,'o' 表示圆圈
# plt.scatter(P0_x, P0_y, color = 'green') # 方法二: scatter 绘图 ,一次一个点
plot_x.append(P0_x) # 方法三: 保存所有黄金点 X坐标,循环结束时候,scatter 绘图
plot_y.append(P0_y) # 方法三: 保存所有黄金点 Y坐标,循环结束时候,scatter 绘图
plt.plot(plot_x[0], plot_y[0], 'bo') # 删除第一个黄金分割点之前,先绘制该点 (换个颜色)
del plot_x[0] # 删除第一个黄金分割点,why? 可以对比一下绘图结果。
del plot_y[0] # 删除第一个黄金分割点,why? 可以对比一下绘图结果。
plt.scatter(plot_x, plot_y, color = 'green') # 方法三: 保存所有黄金点 Y坐标,循环结束时候,scatter 绘图
# 设置标题和坐标轴标签
# plt.title('line and point')
plt.axis('equal') # 保持纵横比相等
# plt.xlabel('x轴')
# plt.ylabel('y轴')
# 显示网格
plt.grid(True)
# 显示图表
plt.show()
4. 结果
如图:
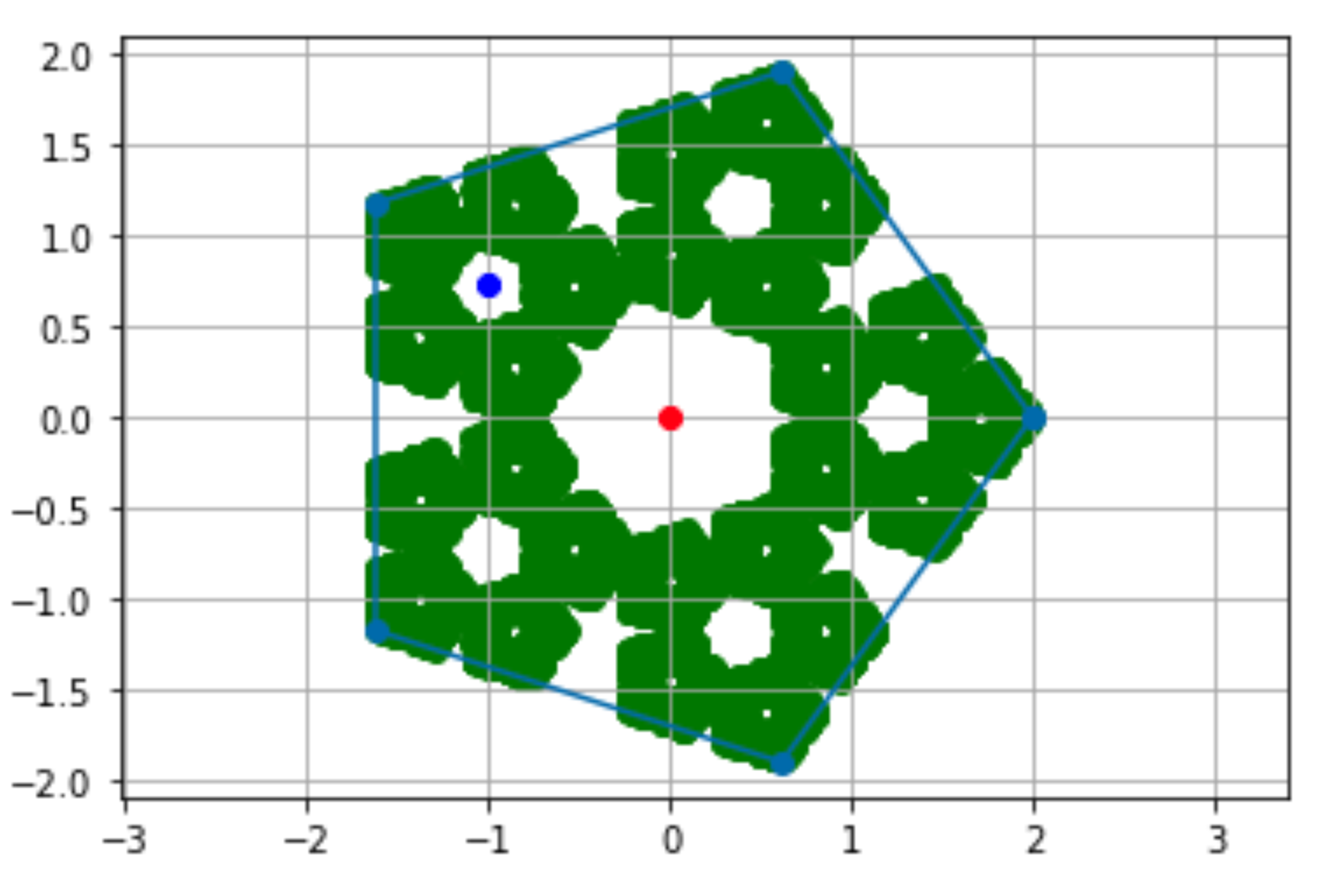
5. 改进
- 将代码 step2 封装为一个函数
# 定义一个函数
def draw_golden(vertices, Number = 40000, Golden = 0.618):
# step 3: 计算黄金分割点,并显示
import matplotlib.pyplot as plt
import random
# vertices 将第1项追加尾部,为了绘图时候首尾相连。注意:执行后vertices长度增加了一个
vertices.append(vertices[0])
X = [Point[0] for Point in vertices] # Point 为顶点
Y = [Point[1] for Point in vertices]
# 使用plot()绘制正多边形
plt.plot(X, Y, marker='o', linestyle='-') # marker='o' 指定点为圆圈,linestyle='-' 指定线为实线
# 单独绘制起始点 ,我们这里设置为原点
plt.plot(0, 0, 'ro') # 'r' 表示红色,'o' 表示圆圈
P0_x, P0_y = 0, 0
plot_x = [] # 方法三:存放所有黄金分割点的 坐标,P0_x
plot_y = [] # 方法三:存放所有黄金分割点的 坐标,P0_y
for i in range(Number):
# 随机指定一个顶点 PN
PN = random.randint(1,len(vertices)-1)
# 求 P0 --- PN 之间的新的点,仍然记为 P0
P0_x = P0_x + (X[PN]- P0_x)* Golden
P0_y = P0_y + (Y[PN]- P0_y)* Golden
# plt.plot(P0_x, P0_y, 'go') # 方法一: plot 绘图 'r' 表示红色,'o' 表示圆圈
# plt.scatter(P0_x, P0_y, color = 'green') # 方法二: scatter 绘图 ,一次一个点
plot_x.append(P0_x) # 方法三: 保存所有黄金点 X坐标,循环结束时候,scatter 绘图
plot_y.append(P0_y) # 方法三: 保存所有黄金点 Y坐标,循环结束时候,scatter 绘图
plt.plot(plot_x[0], plot_y[0], marker='o', color = 'b') # 删除第一个黄金分割点之前,先绘制该点 (换个颜色)
del plot_x[0] # 删除第一个黄金分割点,why? 可以对比一下绘图结果。
del plot_y[0] # 删除第一个黄金分割点,why? 可以对比一下绘图结果。
plt.scatter(plot_x, plot_y, color = 'green') # 方法三: 保存所有黄金点 Y坐标,循环结束时候,scatter 绘图
# 设置标题和坐标轴标签
plt.axis('equal') # 保持纵横比相等
# 显示网格
plt.grid(True)
# 显示图表
plt.show()
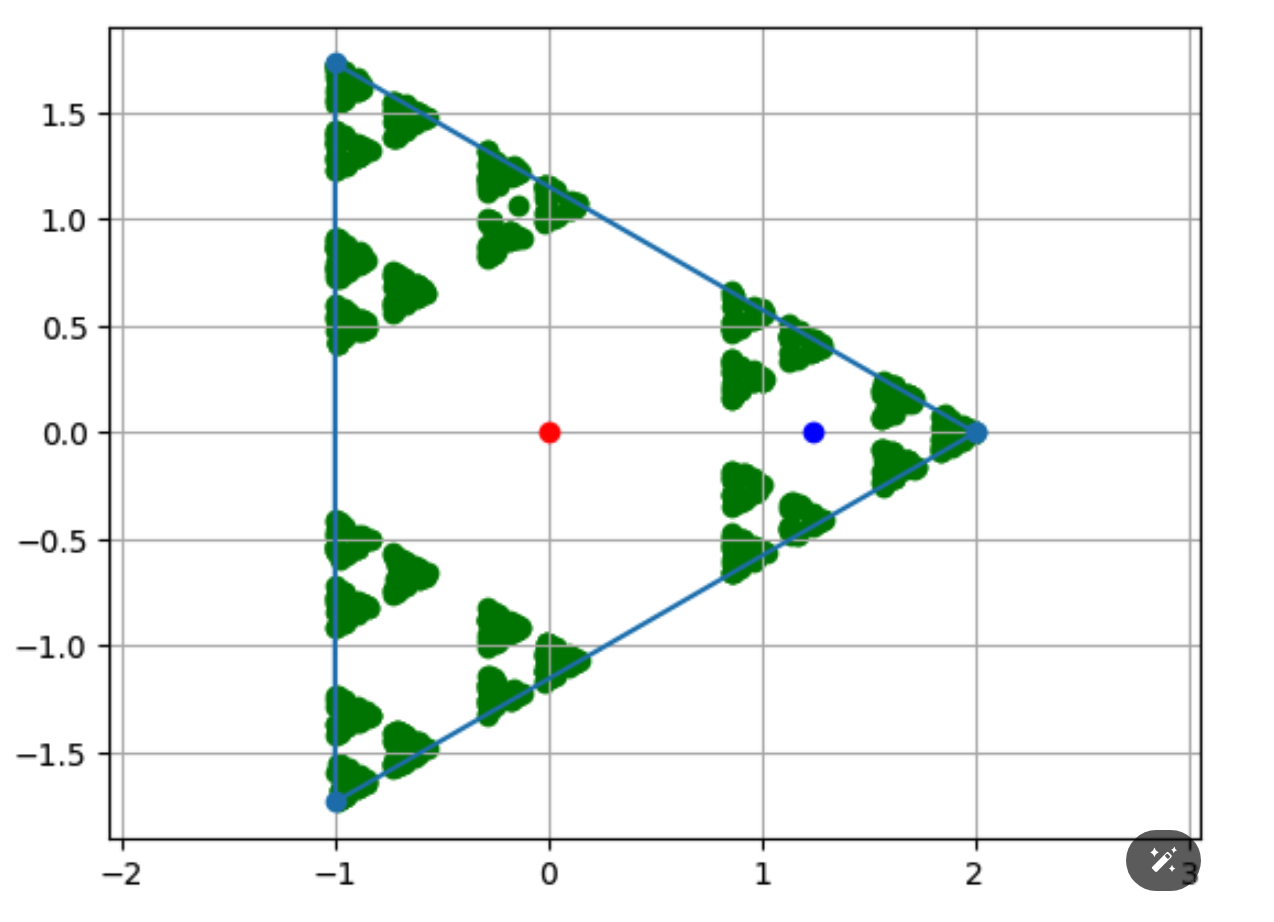
- 测试一: 改变 边数
- 正三边形(等边三角形),结果:
vertices = calculate_pentagon_vertices(2,3)
draw_golden(vertices, 1000)
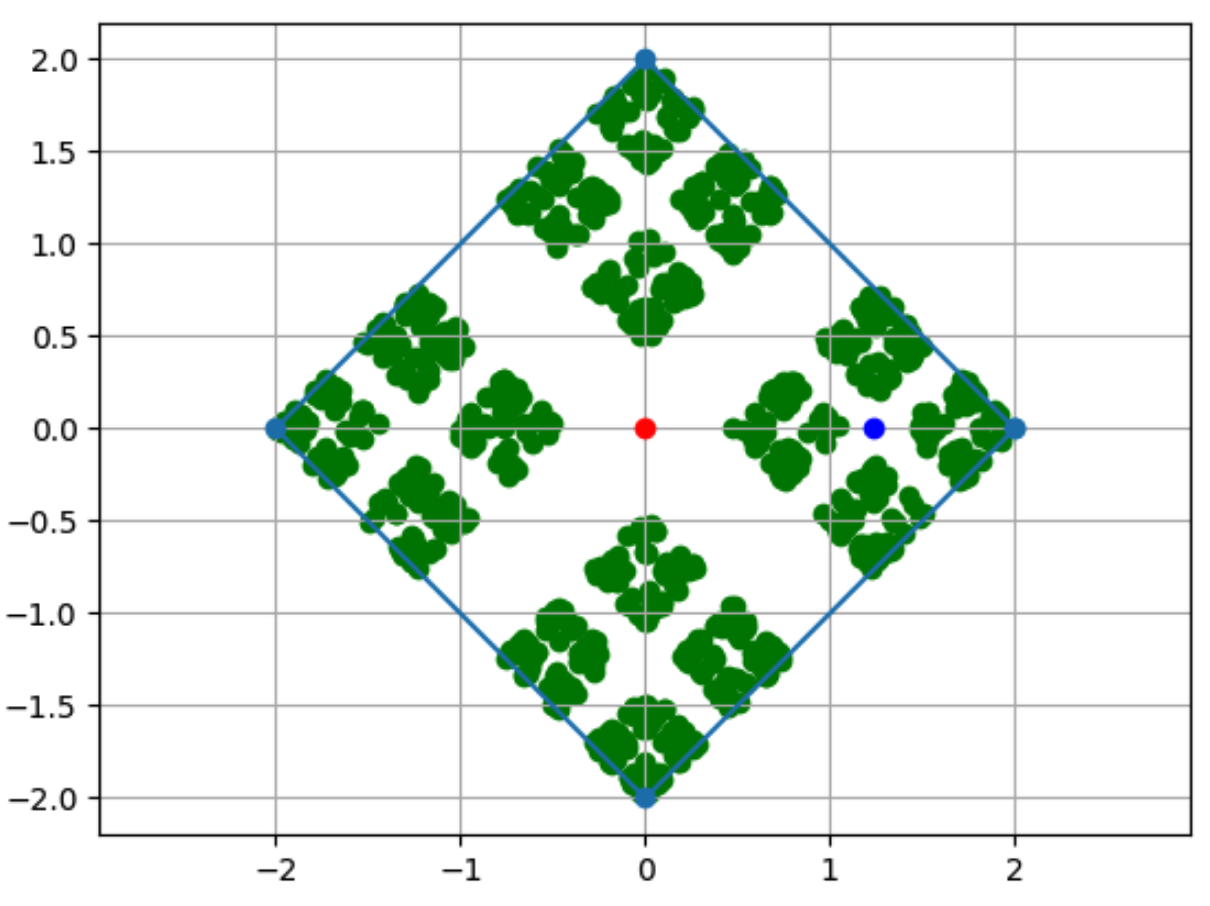
- 四边形
vertices = calculate_pentagon_vertices(2,4)
draw_golden(vertices, 1000)
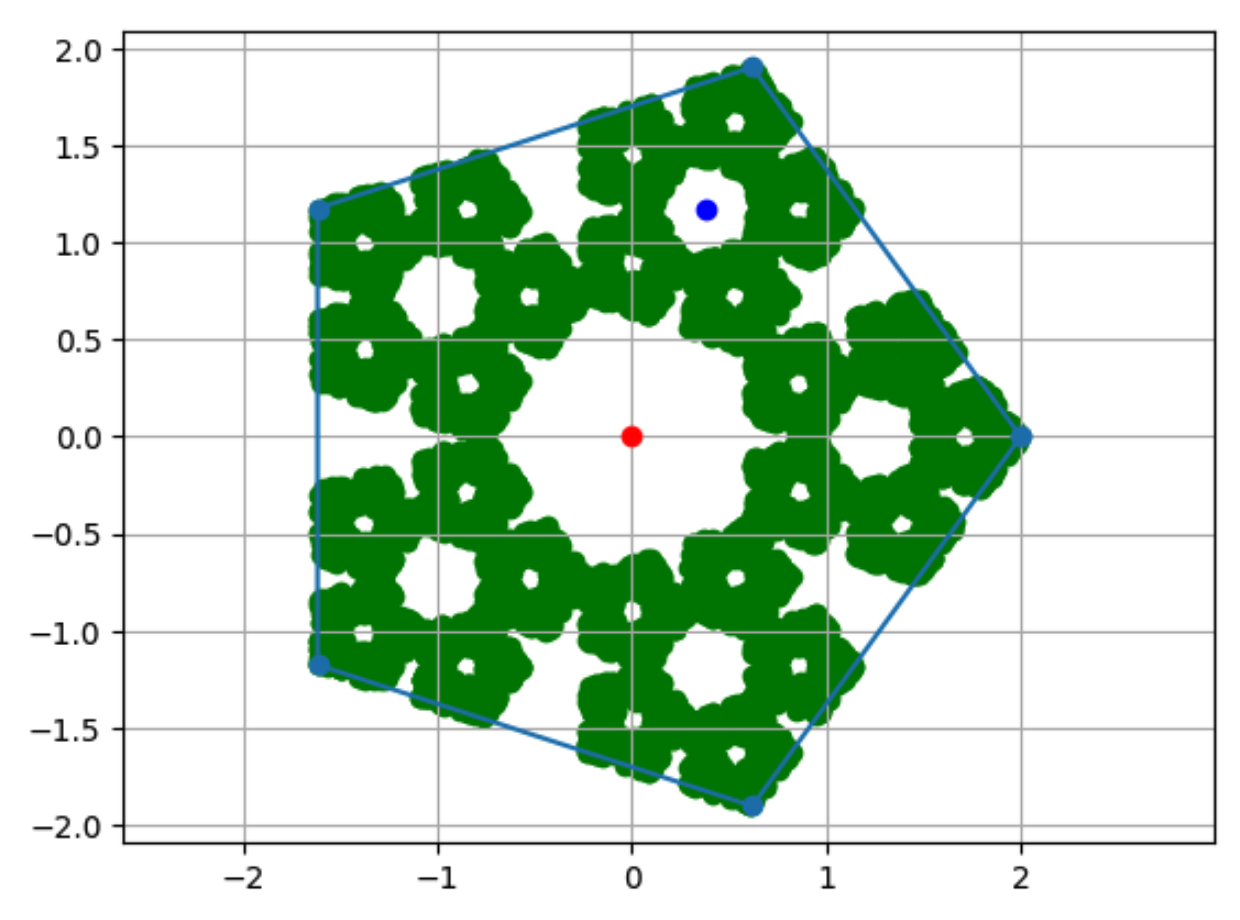
- 正五边形
vertices = calculate_pentagon_vertices(2,5)
draw_golden(vertices, 10000)
- 正六边形
vertices = calculate_pentagon_vertices(2,6)
draw_golden(vertices, 10000)
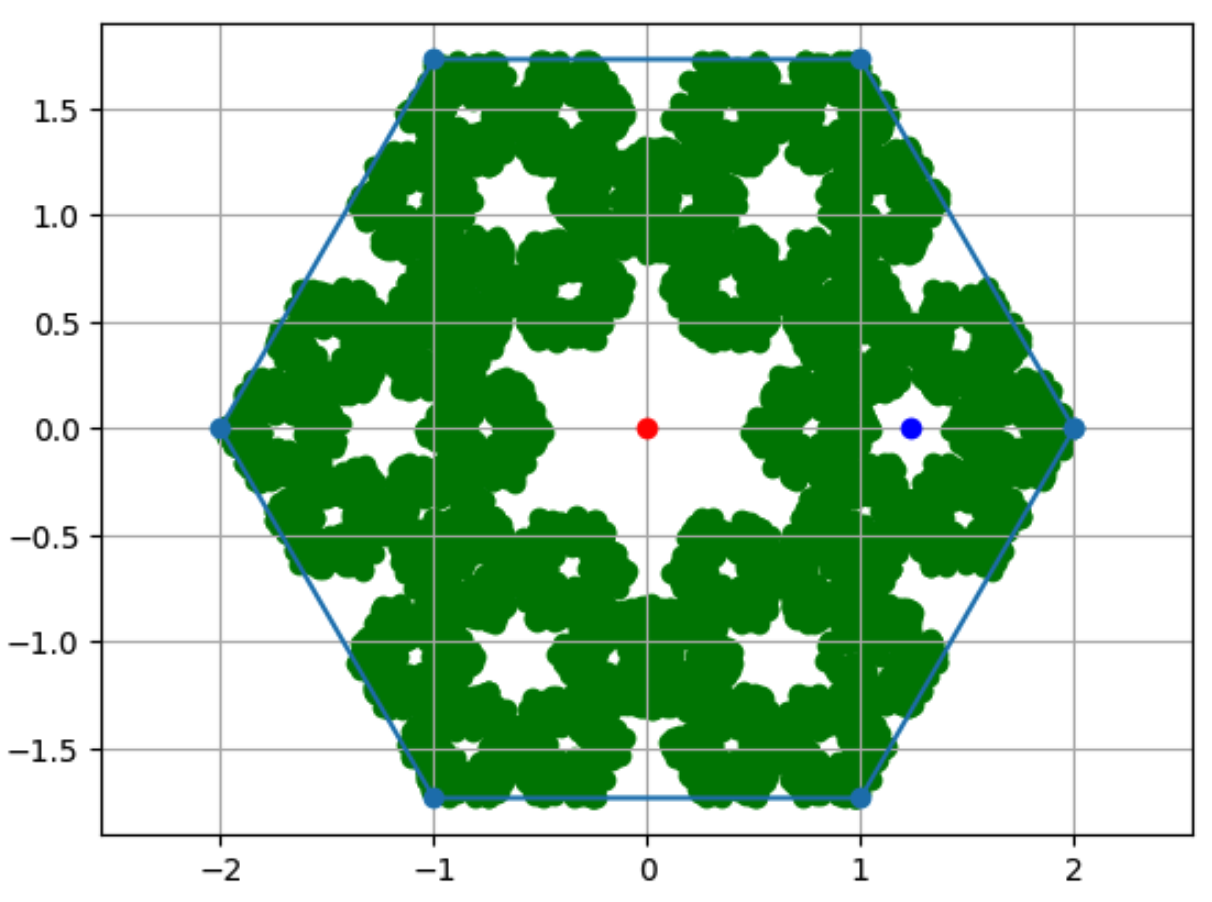
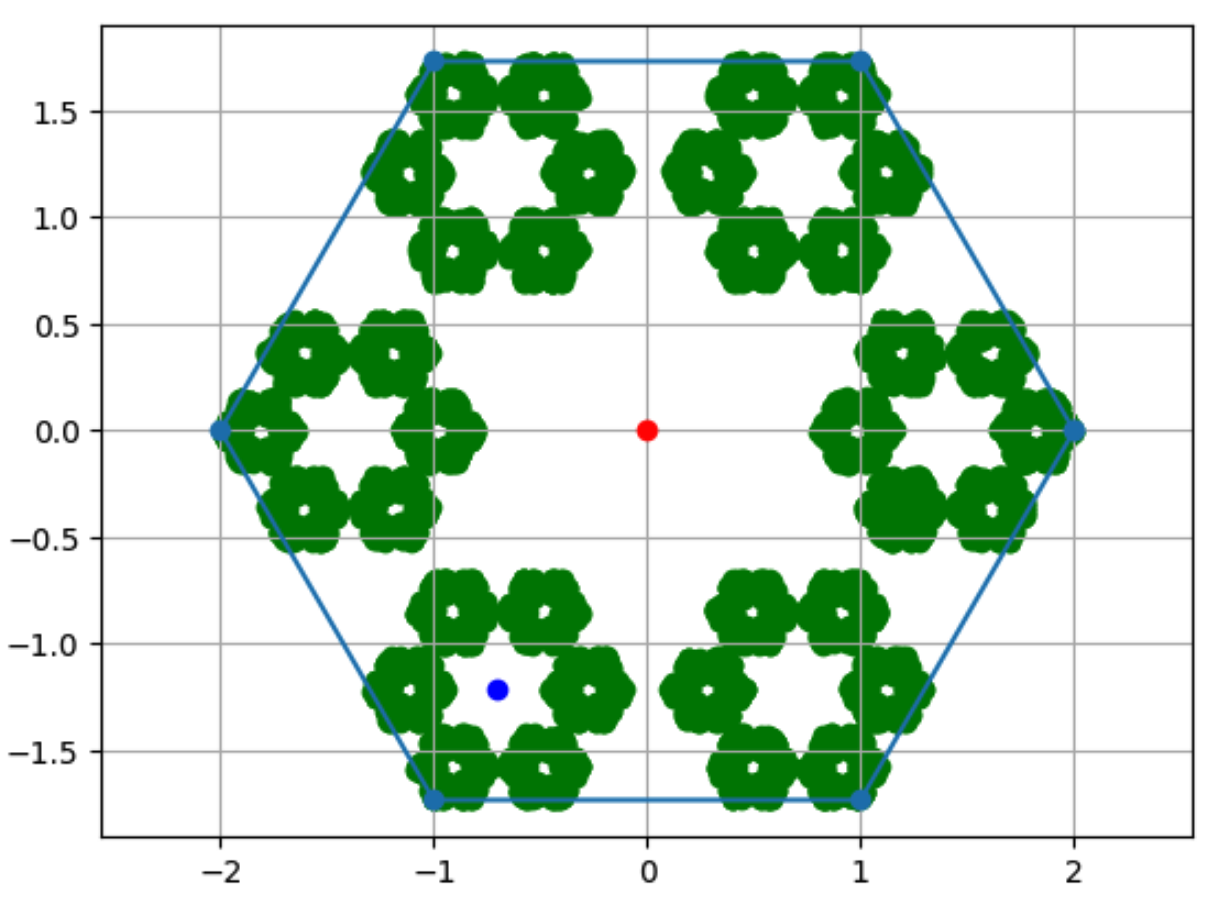
- 测试2: 改变黄金分割参数
vertices = calculate_pentagon_vertices(2,6)
draw_golden(vertices, 10000, 0.7)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号