前缀树

前缀树：
将一个字符串进行拆解，从根节点到叶节点来进行深度延伸，每次延伸都记录一个字符，其最大特点就是可以用来判断字符前缀的问题。

 

原理图：

 

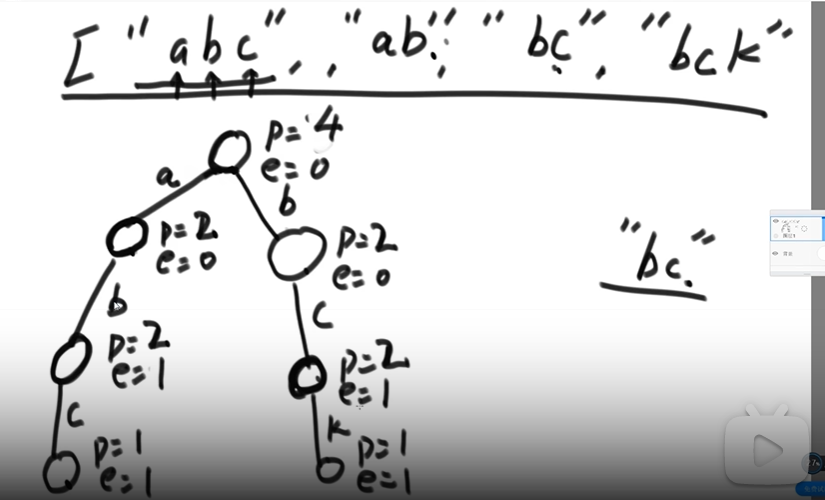
 p为经过这个点的字符串树，e为以这个点为结尾的字符串树

 

代码及解析：
1.基本类的构建：

 1 public static class TrieNode{
 2         int pass;//记录有多少个编码字符经过该节点
 3         int end;//记录有多少个编码字符已该节点为终止点
 4         TrieNode[] nexts;//存放通往下一个节点路径上的字符是什么
 5                          //可以用HashMap<TrieNode,char>来表示，可以更节省空间
 6         
 7         public TrieNode() {
 8             pass = 0;
 9             end = 1;
10             nexts = new TrieNode[26];//0--26分别表示是否有字符a--z的编码
11         }
12     }
13     
14     public static class Trie{
15         TrieNode root;//根节点
16         
17         public Trie() {
18             root = new TrieNode();
19         }
20 　　 }

 

2.插入功能：

 1 //根据所给的字符串来插入构造对应的前缀树
 2         public void Insert(String str) {
 3             if (str == null) {
 4                 return;
 5             }
 6             char[] chs = str.toCharArray();
 7             //从根节点出发构造，且这个字符串一定过根节点，所以root.pass++
 8             TrieNode node = root;
 9             node.pass++;
10             for (int i = 0; i < chs.length; i++) {//遍历字符串中的所有字符进行构造
11                 int index = chs[i] - 'a';
12                 if (node.nexts[index] == null) {//之前没有这条路就开辟一条路
13                     node.nexts[index] = new TrieNode();
14                 }
15                 node = node.nexts[index];//逐层深入进行构造
16                 node.pass++;
17             }
18             node.end++;
19         }

 

3.删除功能：

 1 //在前缀树中删除某一个字符串
 2         public void delete(String str) {
 3             if (Search(str) != 0) {//前缀树中之前插入过str字符串才可进行删除
 4                 char[] chs = str.toCharArray();
 5                 TrieNode node = root;
 6                 node.pass--;
 7                 for (int i = 0; i < chs.length; i++) {
 8                     int index = chs[i] - 'a';
 9                     node = node.nexts[index];
10                     if (--node.pass == 0) {//如果node.pass==0说明已该字符串为前缀的字符没有了,
11                                            //后续的后缀都可以全部释放
12                         node = null;
13                         return;
14                     }
15                 }
16                 node.end--;
17             }
18         }

 

4.查询功能：
(1).查询整个字符串在前缀树插入过几次：

 1 //查询一个字符串在前缀树中插入过几次
 2         public int Search(String str) {
 3             if (str == null) {
 4                 return 0;
 5             }
 6             char[] chs = str.toCharArray();
 7             TrieNode node = root;
 8             for (int i = 0; i < chs.length; i++) {
 9                 int index = chs[i] - 'a';
10                 if (node.nexts[index] == null) {
11                     return 0;
12                 }
13                 node = node.nexts[index];
14             }
15             return node.end;
16         }

(2).查询字符串作为前缀的次数：

 1 //查询当前字符串是做为多少个已插入的字符串的前缀
 2         public int preSearch(String pre) {
 3             if (pre == null) {
 4                 return root.pass;
 5             }
 6             TrieNode node = root;
 7             char[] chs = pre.toCharArray();
 8             for (int i = 0; i < chs.length; i++) {
 9                 int index = chs[i] - 'a';
10                 if (node.nexts[index] == null) {
11                     return 0;
12                 }
13                 node = node.nexts[index];
14             }
15             return node.pass;
16         }

 

posted @ 2022-04-19 22:43  jue1e0  阅读(37)  评论(0)    收藏  举报