奈奎斯特采样定理推导(混叠现象)

1.关于单位冲激函数\(\delta(t)\)
又称为狄拉克函，用\(\delta(t)\)表示，只有在0处值为1，其他地方为0：

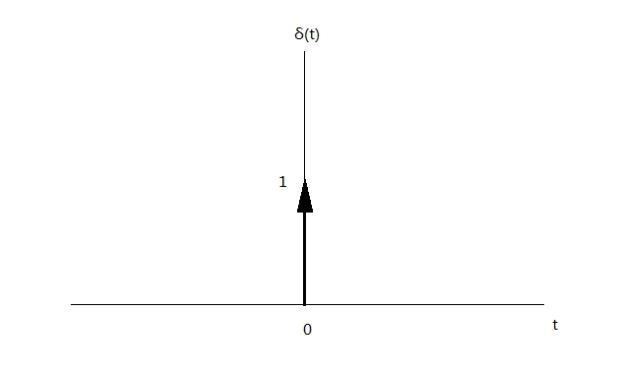
单位冲激函数的性质：与任意时域连续信号相乘后积分为信号在0处的取值，即：
\(\int_{-\infty}^{+\infty}\delta(t)\phi(t)d(t)=\phi(0)\)

2.关于周期冲激函数
令\(p(t)=\sum_{n=-\infty}^\infty \delta(t-nT)\)，得到周期的冲激函数：

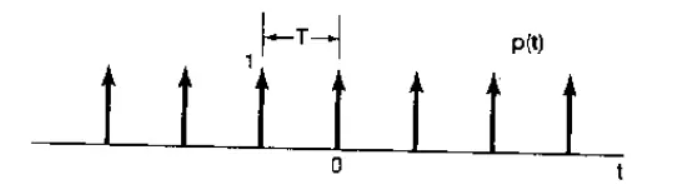
此冲激函数周期是T，可以用此函数与时域连续信号相乘，即可完成采样（ADC过程）；由于周期为T，则采样率\(f_s=\frac{1}{T}\)
周期冲激函数的性质：周期、偶函数，满足傅里叶级数展开条件

3.傅里叶级数展开周期冲激函数
根据傅里叶级数分解【结论】：
\(p(t)=\sum_{n=-\infty}^\infty a_ne^{jn(\frac{2\pi}{T})t}\)
\(a_n=\frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}p(t)e^{-jn(\frac{2\pi}{T})t}dt\)
由于对\(p(t)\)在\(-\frac{T}{2}到\frac{T}{2}\)之间做积分时，等效于对\(\delta(t)\)在\(-\frac{T}{2}到\frac{T}{2}\)之间做积分，故：
\(a_n=\frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}\delta(t)e^{-jn(\frac{2\pi}{T})t}dt\)
根据单位冲激函数的性质得到：
\(a_n=\frac{1}{T}e^{-jn(\frac{2\pi}{T})*0}=\frac{1}{T}\)
故：
\(p(t)=\frac{1}{T}\sum_{n=-\infty}^\infty e^{jn(\frac{2\pi}{T})t}\)

4.对信号进行采样
设时域连续信号为\(x(t)\),AD采样后的信号为\(x_s(t)\),故：
\(x_s(t)=p(t)*x(t)=(\frac{1}{T}\sum_{n=-\infty}^\infty e^{jn(\frac{2\pi}{T})t})*x(t)\)
\(=\frac{1}{T}\sum_{-\infty}^\infty (e^{jn(\frac{2\pi}{T})t}*x(t))\)
根据傅里叶变换对：\(e^{j\omega_s t}*x(t)=X(\omega - \omega_s)\)
对\(x_s(t)\)对傅里叶变换得到：
\(X_s(\omega)=\frac{1}{T}\sum_{-\infty}^\infty X(\omega - \frac{2\pi}{T}n)=\frac{1}{T}\sum_{-\infty}^\infty X(\omega - n\omega_s)\)
其中\(\omega_s=\frac{2\pi}{T}=2\pi f_s\)，\(T\)为周期冲激信号的周期，\(f_s\)为采样率

5.频谱分析
由于：
\(X_s(\omega)=\frac{1}{T}\sum_{-\infty}^\infty X(\omega - n\omega_s)\)
故：AD采样后的信号频谱为原信号频谱频移后的多个累加：

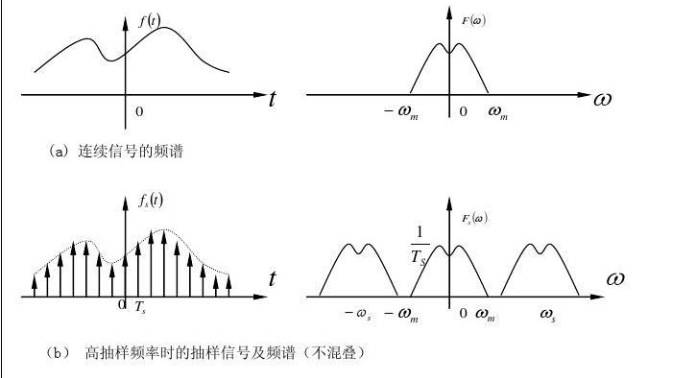
只要保证\(\omega_s\)大于等于\(2\omega_m\)，这些频谱才不会重叠，这个定理叫做奈奎斯特采样定理（也叫低通采样定理）；如果不满足2倍关系时，就会发生重叠，这个现象叫做混叠：

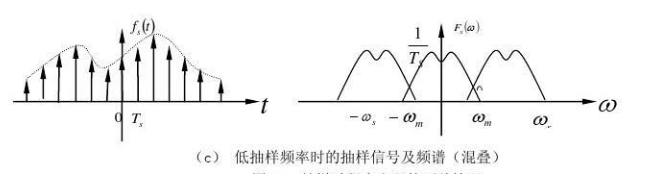
故一般在AD之前，都会设置一个抗混叠滤波器，将不想要的高频信号滤除

6.关于带通采样定理
虽然奈奎斯特定理完全能够搞定任何情况，但是现代通信频率很高，就需要很牛逼的AD，器件可能无法做到。
所以需要想办法在保证能够还原原始信号的前提下，降低AD采样率，这就用到了带通采样定理，这里只说结论：
若信号最高频率为信号带宽的整数倍时，采样频率只需大于信号带宽的两倍，而不会发生频谱混叠
推导参考：https://zhuanlan.zhihu.com/p/585401909