Matlab进行FFT变换
1、代码
close all; %先关闭所有图片 Adc=2; %直流分量幅度 A1=3; %频率F1信号的幅度 A2=1.5; %频率F2信号的幅度 F1=50; %信号1频率(Hz) F2=75; %信号2频率(Hz) Fs=256; %采样频率(Hz),根据奈奎斯特定理:采样频率必须大于2倍信号频率 P1=-30; %信号1相位(度) P2=90; %信号相位(度) N=256; %采样点数,为了方便进行FFT运算,通常N取2的整数次方 t=[0:1/Fs:N/Fs]; %采样时刻 S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180); %信号 plot(S); %显示原始信号 title('原始信号'); figure; Y = fft(S,N); %做FFT变换,结果为N点的复数,每一个点就对应着一个频率点 Ayy = (abs(Y)); %取模运算,对数值是求绝对值,对复数是求幅值。这里就是复数转幅度值 plot(Ayy(1:N)); %显示原始的FFT模值结果 title('FFT 模值'); figure; Ayy=Ayy/(N/2); %换算成实际的幅度,针对半频谱 Ayy(1)=Ayy(1)/2; %直流和奈奎斯特频率处还需要/2 F=([1:N]-1)*Fs/N; %换算成实际的频率值,采到每个点对应的频率 plot(F(1:N/2),Ayy(1:N/2)); %显示换算后的FFT模值结果 title('幅度-频率曲线图'); figure; Pyy=[1:N/2]; for i=1:N/2 Pyy(i)=phase(Y(i)); %计算相位 Pyy(i)=Pyy(i)*180/pi; %换算为角度 end; plot(F(1:N/2),Pyy(1:N/2)); %显示相位图 title('相位-频率曲线图');
2、结果
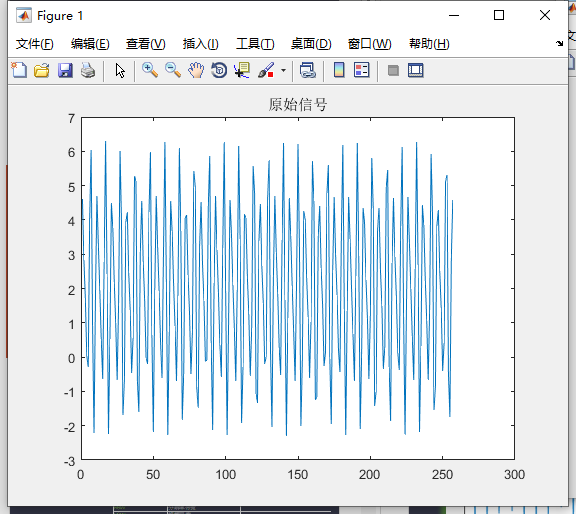
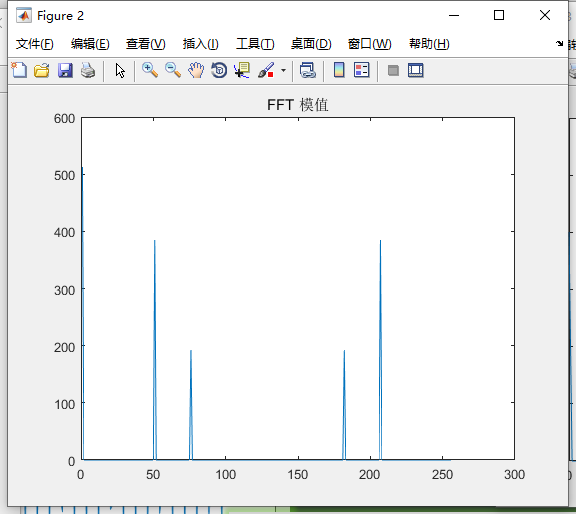
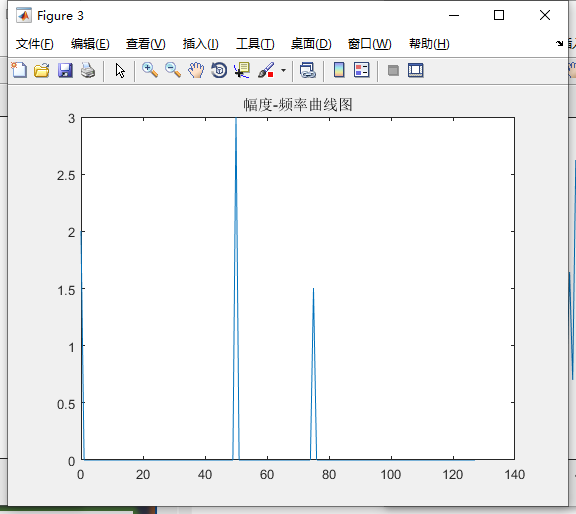

长风破浪会有时,直挂云帆济沧海!
可通过下方链接找到博主
https://www.cnblogs.com/judes/p/10875138.html



