梯度下降实现案例（含python代码）

基础：损失函数的定义，参考http://blog.csdn.net/l18930738887/article/details/50615029

目标：已知学习样本，求解预测函数的系数，希望损失函数取到最小值。

一、原理介绍：

假设我们已知门店销量为

 

门店数X

实际销量Y

1

13

2

14

3

20

4

21

5

25

6

30

我们如何预测门店数X与Y的关系式呢？假设我们设定为线性：Y=a0+a1X

接下来我们如何使用已知数据预测参数a0和a1呢？这里就是用了梯度下降法：

左侧就是梯度下降法的核心内容，右侧第一个公式为假设函数，第二个公式为损失函数。

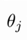
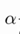
其中 表示假设函数的系数，为学习率。

对我们之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即：

直观的表示，如下：

（取自斯坦福大学机器学习）

二、python代码实现：（以下代码是鲁棒性不高，可以看神经网络的梯度下降http://blog.csdn.net/l18930738887/article/details/50724478。）

[python] view plain copy
 
  1. </pre><pre>  

 

[python] view plain copy
 
  1. import sys  
  2. #Training data set  
  3. #each element in x represents (x1)  
  4. x = [1,2,3,4,5,6]  
  5. #y[i] is the output of y = theta0+ theta1 * x[1]  
  6. y = [13,14,20,21,25,30]  
  7. #设置允许误差值  
  8. epsilon = 1  
  9. #学习率  
  10. alpha = 0.01  
  11. diff = [0,0]  
  12. max_itor = 20  
  13. error1 = 0  
  14. error0 =0  
  15. cnt = 0  
  16. m = len(x)  
  17. #init the parameters to zero  
  18. theta0 = 0  
  19. theta1 = 0  
  20. while 1:  
  21.     cnt=cnt+1  
  22.     diff = [0,0]  
  23.     for i in range(m):  
  24.         diff[0]+=theta0+ theta1 * x[i]-y[i]  
  25.         diff[1]+=(theta0+theta1*x[i]-y[i])*x[i]  
  26.     theta0=theta0-alpha/m*diff[0]  
  27.     theta1=theta1-alpha/m*diff[1]  
  28.     error1=0  
  29.     for i in range(m):  
  30.         error1+=(theta0+theta1*x[i]-y[i])**2  
  31.     if abs(error1-error0)< epsilon:  
  32.         break  
  33.     print'theta0 :%f,theta1 :%f,error:%f'%(theta0,theta1,error1)  
  34.     if cnt>20:  
  35.         print 'cnt>20'  
  36.         break  
  37. print'theta0 :%f,theta1 :%f,error:%f'%(theta0,theta1,error1)  



 

结果现实：

[plain] view plain copy
 
  1. <pre style="box-sizing: border-box; overflow: auto; font-size: 14px; padding: 0px; margin-top: 0px; margin-bottom: 0px; line-height: 17.0001px; word-break: break-all; word-wrap: break-word; border: 0px; border-radius: 0px; white-space: pre-wrap; vertical-align: baseline; rgb(255, 255, 255);"><pre name="code" class="plain">theta0 :0.205000,theta1 :0.816667,error:1948.212261  
  2. theta0 :0.379367,theta1 :1.502297,error:1395.602361  
  3. theta0 :0.527993,theta1 :2.077838,error:1005.467313  
  4. theta0 :0.654988,theta1 :2.560886,error:730.017909  
  5. theta0 :0.763807,theta1 :2.966227,error:535.521394  
  6. theta0 :0.857351,theta1 :3.306283,error:398.166976  
  7. theta0 :0.938058,theta1 :3.591489,error:301.147437  
  8. theta0 :1.007975,theta1 :3.830615,error:232.599138  
  9. theta0 :1.068824,theta1 :4.031026,error:184.147948  
  10. theta0 :1.122050,theta1 :4.198911,error:149.882851  
  11. theta0 :1.168868,theta1 :4.339471,error:125.631467  
  12. theta0 :1.210297,theta1 :4.457074,error:108.448654  
  13. theta0 :1.247197,theta1 :4.555391,error:96.255537  
  14. theta0 :1.280286,theta1 :4.637505,error:87.584709  
  15. theta0 :1.310171,theta1 :4.706007,error:81.400378  
  16. theta0 :1.337359,theta1 :4.763073,error:76.971413  
  17. theta0 :1.362278,theta1 :4.810533,error:73.781731  
  18. theta0 :1.385286,theta1 :4.849922,error:71.467048  
  19. theta0 :1.406686,theta1 :4.882532,error:69.770228  
  20. theta0 :1.426731,theta1 :4.909448,error:68.509764  
  21. theta0 :1.445633,theta1 :4.931579,error:67.557539  
  22. cnt>20  
  23. theta0 :1.445633,theta1 :4.931579,error:67.557539  



 






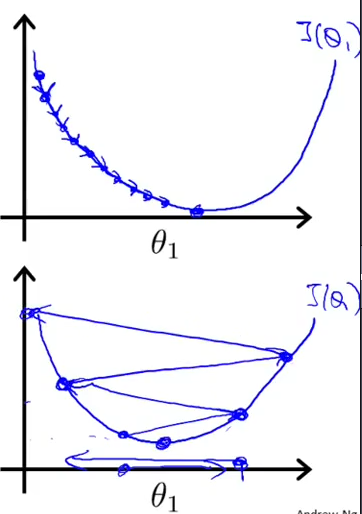
可以看到学习率在0.01时，error会正常下降。图形如下：（第一张图是学习率小的时候，第二张图就是学习率较大的时候）


 






所以我们再调整一下新的学习率看看是否能看到第二张图：


我们将学习率调整成了0.3的时候得到以下结果：


 






[plain] view plain copy

 








    

  1. theta0 :6.150000,theta1 :24.500000,error:38386.135000  
    2. 

  2. theta0 :-15.270000,theta1 :-68.932500,error:552053.226569  
    3. 

  3. theta0 :67.840125,theta1 :285.243875,error:7950988.401277  
    4. 

  4. theta0 :-245.867981,theta1 :-1059.347887,error:114525223.507401  
    5. 

  5. theta0 :946.357695,theta1 :4043.346381,error:1649619133.261223  
    6. 

  6. theta0 :-3576.913313,theta1 :-15323.055232,error:23761091159.680252  
    7. 

  7. theta0 :13591.518674,theta1 :58177.105053,error:342254436006.869995  
    8. 

  8. theta0 :-51565.747234,theta1 :-220775.317546,error:4929828278909.234375  
    9. 

  9. theta0 :195724.210360,theta1 :837920.911885,error:71009180027939.656250  
    10. 

  10. theta0 :-742803.860227,theta1 :-3180105.158068,error:1022815271242165.875000  
    11. 

  11. theta0 :2819153.863813,theta1 :12069341.864380,error:14732617369683060.000000  
    12. 

  12. theta0 :-10699395.102930,theta1 :-45806250.675551,error:212208421856953728.000000  
    13. 

  13. theta0 :40606992.787278,theta1 :173846579.256281,error:3056647245837464576.000000  
    14. 

  14. theta0 :-154114007.118001,theta1 :-659792674.286440,error:44027905696333684736.000000  
    15. 

  15. theta0 :584902509.168162,theta1 :2504083725.690765,error:634177359734604038144.000000  
    16. 

  16. theta0 :-2219856149.407590,theta1 :-9503644836.328783,error:9134682134868024885248.000000  
    17. 

  17. theta0 :8424927779.709908,theta1 :36068788150.345154,error:131575838248146814631936.000000  
    18. 

  18. theta0 :-31974778105.915466,theta1 :-136890372077.920685,error:1895216599231190653730816.000000  
    19. 

  19. theta0 :121352546013.825867,theta1 :519534337912.329712,error:27298674329760760684609536.000000  
    20. 

  20. theta0 :-460564272592.117981,theta1 :-1971767072878.787598,error:393209736799816196514906112.000000  
    21. 

  21. theta0 :1747960435714.394287,theta1 :7483365594965.919922,error:5663787744653302294061776896.000000  
    22. 

  22. cnt>20  
    23. 

  23. theta0 :1747960435714.394287,theta1 :7483365594965.919922,error:5663787744653302294061776896.000000  
    24. 





可以看到theta0和theta1都在跳跃，与预期相符。


 


上文使用的是批量梯度下降法，如遇到大型数据集的时候这种算法非常缓慢，因为每次迭代都需要学习全部数据集，后续推出了随机梯度下降，其实也就是抽样学习的概念。


 






            

            
posted @ 
2018-05-07 10:48 
jude_python 
阅读(805) 
评论(0) 
编辑 
收藏 
举报