梯度下降法求解线性回归的python实现及其结果可视化（一）

编者注：本文包含了使用Python2.X读取数据、数据处理、作图，构建梯度下降法函数求解一元线性回归，并对结果进行可视化展示，是非常综合的一篇文章，包含了Python的数据操作、可视化与机器学习等内容。学习了这一篇文章就大概了解或掌握相关Python编程与数据分析等内容。另外，本文还巧妙地进行了一个设计，这使得本文Python代码也可用于多元线性回归，这是区别与现有网络上大多数梯度下降法求解线性回归的Python实现不同，具体会在文中说明。

一、梯度下降法与回归分析

梯度下降法则是一种最优化算法，它是用迭代的方法求解目标函数得到最优解，是在cost function（成本函数）的基础上，利用梯度迭代求出局部最优解。在这里关于梯度下降法不做过多介绍，相关资料已经很多且后边还会结合构建的函数进行分析，借用网上常用的一个比喻去直观解释。

比如，我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

回归在数学上来说是给定一个点集，能够用一条曲线去拟合之，如果这个曲线是一条直线，那就被称为线性回归，线性回归大家应该很熟悉，在这里也不过多解释，后边构造代码的时候也会去分析一些，在回归分析中，只包括一个自变量和一个因变量，即y=a+bx+u称为一元线性回归分析。若是包含多个因变量则是多元线性回归，即y=a+b1x1+b2x2+…+bnxn+u。
二、用Python读取所要使用的数据

数据来自于UCI的机器学习数据库中的Auto-mpg汽车燃料效率（mpg），共有398个样本，以及9个变量，分别是mpg（燃料效率）、cylinders（发动机里的气缸数量）、displacement（发动机的位移）、horsepower（发动机的马力，有缺失值）、weight（汽车的重量）、acceleration（汽车的加速性能）、model year（汽车类型的生产年份）、car name（汽车品牌）等等。在导入numpy、pandas、matplotlib、math等数据处理相关模块后，通过读取url来导入数据，部分数据网页呈现形式截图如下：

 
Paste_Image.png

网页数据呈现形式有两个需要注意的地方（这也是许多UCI数据的特点）：一是没有表头，我们就在代码中构建name列表并加入pd.read_csv中，否则的话数据第一行就会作为表头；二是数据间用空格来间隔，我们就在pd.read_cs加入delim_whitespace=True来分列，默认分隔符为逗号。
其代码如下：

import numpy as np  
import pandas as pd  
import matplotlib.pyplot as plt 
import math

url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data'
names =["mpg","cylinders","displacement","horsepower",
        "weight","acceleration","model year","origin","car name"]
cars = pd.read_csv(url, delim_whitespace=True,names=names)#值与值之间，使用空白字符来指定你想要的分隔符
cars.head(5)

得到结果：


 
Paste_Image.png

对其中的mpg与acceleration绘制散点图如下：

plt.scatter(cars["mpg"] ,cars["acceleration"]) #mpg燃料效率；acceleration汽车的加速性能
plt.xlabel('mpg')
plt.ylabel('acceleration')#设置坐标轴标签
plt.show()
 
Paste_Image.png

三、数据处理——构建X、Y变量
将'mpg','weight'列单独拿出来，作为构建回归分析的X、Y变量，代码如下：

data = cars[['mpg','acceleration']]#选取表格中的'mpg','weight'列
data.insert(0, 'Ones', 1) #在data第1-2列之间插入全是1的一列数
# set X (training data) and y (target variable)
cols = data.shape[1]  #计算data的列数，在这里cols为3
X = data.iloc[:,0:cols-1]  
y = data.iloc[:,cols-1:cols]

在这里可能很多人会有疑问：为什么要插入一列全是1的数据？为什么还要采用iloc选取列的函数来重新定义X、y，本文分析的变量'mpg','weight'不是已经有了么？
因此，在这里我们需要对回归分析模型着重说一下。事实上，无论是一元线性回归如y=β0+β1x，还是多元线性回归如y=β0+β1x1+β2x2+…+βnxn+u，都可以用矩阵形式表示：


 
Paste_Image.png

对于一元线性回归，那么上数矩阵就是取k=2，X变量也就是前两列，即1和X21—X2n的矩阵，这就是为什么要在data中插入全是1的一列意义所在，然后用iloc选取前两列为X变量，最后一列为y变量。
四、先用最小二乘法求解回归并计算损失函数
为了比较梯度下降法的求解结果，在这里先用最小二乘法求解回归，具体求解过程不再细述，其求解公式为：


 
Paste_Image.png
线性回归的平方差损失函数为：
 
Paste_Image.png
代码如下 
X = np.matrix(X.values)  
y = np.matrix(y.values)  #首先要把变量由data frames 转变为矩阵形式
from numpy.linalg import inv
from numpy import dot
theta_n = dot(dot(inv(dot(X.T, X)), X.T), y) # theta = (X'X)^(-1)X'Y
print theta_n

def computeCost(X, y, theta):  
    inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
X.shape, theta_n.shape, y.shape
lr_cost = computeCost(X, y, theta_n.T)
print(lr_cost)

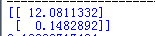
得到结果为：theta_n=[12.0811332, 0.1482892]T，为2*1（2行1列）矩阵，所以在计算损失函数中要进行转置（theta_n.T）。因为涉及到矩阵计算，所以要用“X.shape, theta_n.shape, y.shape”命令看一下三个矩阵的形式。
得到的损失值lr_cost为3.12288717494。

 

def gradientDescent(X, y, theta, alpha, iters):
temp = np.matrix(np.zeros(theta.shape))#构建零值矩阵
parameters = int(theta.ravel().shape[1])#计算需要求解的参数个数
cost = np.zeros(iters) #构建iters个0的数组

for i in range(iters):
error = (X * theta.T) - y #计算hθ(x)-y

for j in range(parameters):
term = np.multiply(error, X[:,j])#计算两矩阵(hθ(x)-y)x
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))

theta = temp
cost[i] = computeCost(X, y, theta)

return theta, cost

theta,cost分别为：

接下来，绘制拟合曲线

alpha = 0.001 

iters = 100000
theta = np.matrix(np.array([0,0]))
# perform gradient descent to "fit" the model parameters
g, cost = gradientDescent(X, y, theta, alpha, iters)
g
computeCost(X, y, g)

x = np.linspace(data.mpg.min(), data.mpg.max(), 100)
print(x)
f = g[0, 0] + (g[0, 1] * x)
print(f)
fig,ax = plt.subplots(figsize=(8,6))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.mpg, data.acceleration, label='Traning Data') #散点
ax.legend(loc=2)
ax.set_xlabel('mpg')
ax.set_ylabel('acceleration')

 最后绘制代价曲线

fig, bx = plt.subplots(figsize=(8,6))
bx.plot(np.arange(iters), cost, 'r')
bx.set_xlabel('Iterations')
bx.set_ylabel('Cost')
bx.set_title('Error vs. Training Epoch')
plt.show()

 

 

 

可知，iterations为13000-2000时代价曲线基本稳定。

 

 

 

 

 

完整代码地址：http://note.youdao.com/noteshare?id=4b0d35625b292621bdc8f31f31effa82**
写作不易，特别是技术类的写作，请大家多多支持，关注、点赞、转发等等。
参考文献：

  1. Machine Learning Exercises In Python,Part 1,
    http://www.johnwittenauer.net/machine-learning-exercises-in-python-part-1/**
  2. （吴恩达笔记 1-3）——损失函数及梯度下降
    http://blog.csdn.net/wearge/article/details/77073142?locationNum=9&fps=1**
  3. 梯度下降法求解线性回归之python实现
    http://blog.csdn.net/just_do_it_123/article/details/51056260



作者：博观厚积
链接：https://www.jianshu.com/p/82c7b3ceff66
來源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

posted @ 2018-05-06 21:45  jude_python  阅读(8611)  评论(0)  编辑  收藏  举报