梯度下降原理及Python实现
梯度下降算法是一个很基本的算法,在机器学习和优化中有着非常重要的作用,本文首先介绍了梯度下降的基本概念,然后使用python实现了一个基本的梯度下降算法。梯度下降有很多的变种,本文只介绍最基础的梯度下降,也就是批梯度下降。
实际应用例子就不详细说了,网上关于梯度下降的应用例子很多,最多的就是NG课上的预测房价例子:
假设有一个房屋销售的数据如下:
面积(m^2) 销售价钱(万元)
| 面积(m^2) | 销售价钱(万元) |
|---|---|
| 123 | 250 |
| 150 | 320 |
| 87 | 180 |
根据上面的房价我们可以做这样一个图:

于是我们的目标就是去拟合这个图,使得新的样本数据进来以后我们可以方便进行预测: 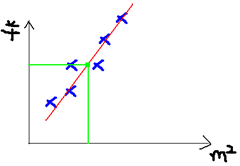
对于最基本的线性回归问题,公式如下: 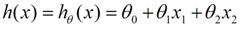
x是自变量,比如说房子面积。θ是权重参数,也就是我们需要去梯度下降求解的具体值。
在这儿,我们需要引入损失函数(Loss function 或者叫 cost function),目的是为了在梯度下降时用来衡量我们更新后的参数是否是向着正确的方向前进,如图损失函数(m表示训练集样本数量): 
下图直观显示了我们梯度下降的方向,就是希望从最高处一直下降到最低出: 
梯度下降更新权重参数的过程中我们需要对损失函数求偏导数: 
求完偏导数以后就可以进行参数更新了: 
伪代码如图所示: 
好了,下面到了代码实现环节,我们用Python来实现一个梯度下降算法,求解:
y=2x1+x2+3y=2x1+x2+3
,也就是求解:
y=ax1+bx2+cy=ax1+bx2+c
中的a,b,c三个参数 。
下面是代码:
import numpy as np
import matplotlib.pyplot as plt
#y=2 * (x1) + (x2) + 3
rate = 0.001
x_train = np.array([ [1, 2], [2, 1], [2, 3], [3, 5], [1, 3], [4, 2], [7, 3], [4, 5], [11, 3], [8, 7] ])
y_train = np.array([7, 8, 10, 14, 8, 13, 20, 16, 28, 26])
x_test = np.array([ [1, 4], [2, 2], [2, 5], [5, 3], [1, 5], [4, 1] ])
a = np.random.normal()
b = np.random.normal()
c = np.random.normal()
def h(x):
return a*x[0]+b*x[1]+c
for i in range(10000):
sum_a=0
sum_b=0
sum_c=0
for x, y in zip(x_train, y_train):
sum_a = sum_a + rate*(y-h(x))*x[0]
sum_b = sum_b + rate*(y-h(x))*x[1]
sum_c = sum_c + rate*(y-h(x))
a = a + sum_a
b = b + sum_b
c = c + sum_c
plt.plot([h(xi) for xi in x_test])
print(a)
print(b)
print(c)
result=[h(xi) for xi in x_train]
print(result)
result=[h(xi) for xi in x_test]
print(result)
plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
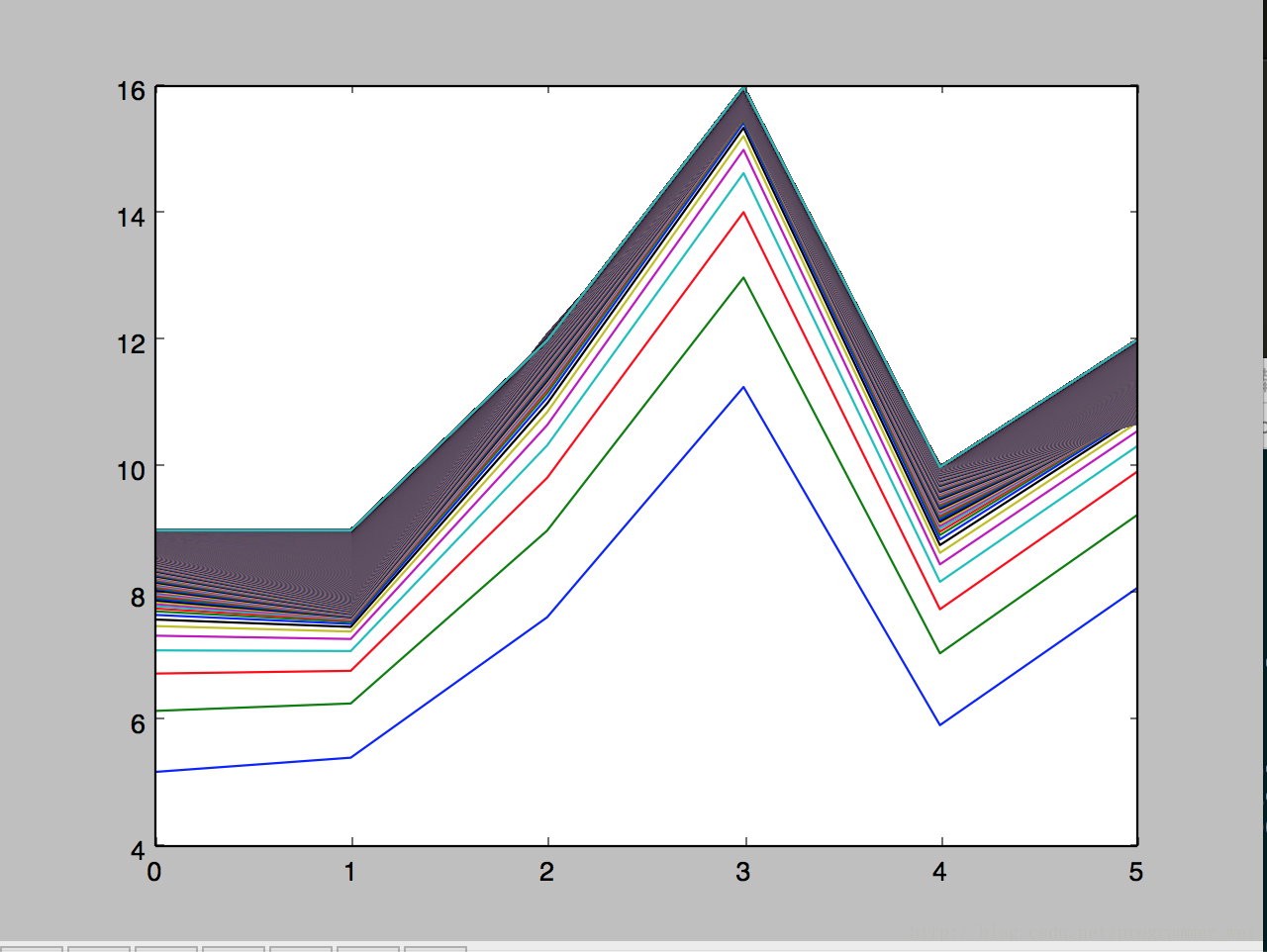
x_train是训练集x,y_train是训练集y, x_test是测试集x,运行后得到如下的图,图片显示了算法对于测试集y的预测在每一轮迭代中是如何变化的:
我们可以看到,线段是在逐渐逼近的,训练数据越多,迭代次数越多就越逼近真实值。