APIO2013 T3 Tasksauthor

首先解决 \(\text{SSSP}\) 问题的六个点。我们观察给出的三个算法。

\(Floyd\) 的运行次数是死的 \(n^3\) 次，超了就挂，和边连接情况以及询问无关。

\(Bellman-Ford\) 的理论复杂度是 \(O(nm)\)，每次都要跑 \(Q\) 次。

\(Dijkstra\) 的算法是 \(O(m\log n)\)，没什么意义，正权边随便过，负权边不能过的情况需要特殊构造。

（这道题几乎全部的难点在于 \(test 4\)，需要对 \(Dijkstra\) 的一些内容有着深入的理解）

1

\(\text{test1}\) 用 \(Dij\) 卡 \(Floyd\)。凡是卡 \(Floyd\) 的，都可以用一个 \(101\) 个点，\(0\) 条边的空图去卡，最后要有一次询问，就问 \(0\) 到 \(1\)。在这个数据下 \(Dij\) 和 \(Bf\) 根本就不工作，随便跑，\(Floyd\) 会被卡满。数字个数 \(104\)。

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout<<100<<endl;
	rp(i,101)cout<<0<<endl;
	cout<<1<<endl;
	cout<<"1 2"<<endl;
	return 0;
}
//Crayan_r

2

\(\text{test2}\) 用 \(Floyd\) 卡 \(Bf\)。首先，点数不能超过 \(100\)，就可以放过 \(Floyd\)。然后考虑 \(Bf\) 怎么卡。我们发现它一共会跑许多轮，每次都是从 \(0\) 到 \(n-1\) 依次更新扫描所有边。那么我们的目标就是把跑的轮数卡满。假设我们需要的最短路是 \(x\) 到 \(y\)，那么理想状态就是每轮只能沿着最短路更新一次。

那么我们就考虑怎么卡。发现只要下一轮要走的新点编号比原先的点小，就必须下一轮再更新。这样我们连 \(99\) 到 \(0\) 的链，然后随便连一些别的权值很大的边，就可以把复杂度卡到 \(nm\)。

vt<pii>vv[105];
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout<<100<<endl;
	vv[0].pb({99,1});
	rep(i,2,99)vv[i].pb({i-1,1});
	int cnt=0;
	rep(i,1,99){
		rep(j,i+1,99){
			vv[i].pb({j,999999});
			cnt++;
			if(cnt==950)break;
		}if(cnt==950)break;
	}
	rd(i,100){
		cout<<vv[i].size()<<" ";
		for(auto j:vv[i])cout<<j.first<<" "<<j.second<<" ";
		cout<<endl;
	}
	cout<<10<<endl;
	rd(_,10)cout<<0<<" "<<1<<endl;
	return 0;
}
//Crayan_r

3

\(\text{test3}\) 用 \(Bf\) 卡 \(Floyd\)，直接用第一次的数据即可。

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	freopen("f.out","w",stdout);
	cout<<100<<endl;
	rp(i,101)cout<<0<<endl;
	cout<<1<<endl;
	cout<<"1 2"<<endl;
	return 0;
}
//Crayan_r

4

卡 \(Dijkstra\)。\(Dij\) 怎么卡？在正权图上 \(Dij\) 怎么也不可能跑不过 \(Floyd\)，那就只能去打负权边的主意了。

然后看到这个数字个数限制还非常捉急，这么一点数字，每个点还至少要连一条边，匀下来点数只有 \(40\) 多，怎么办？卡成平方还不够，只能往指数级上卡。

我们来看 \(Dij\) 的复杂度证明，应用了正权边的关键证明就是每个点出堆的时候当前路等于最短路。那么我们就额可以基于这一点进行设计。

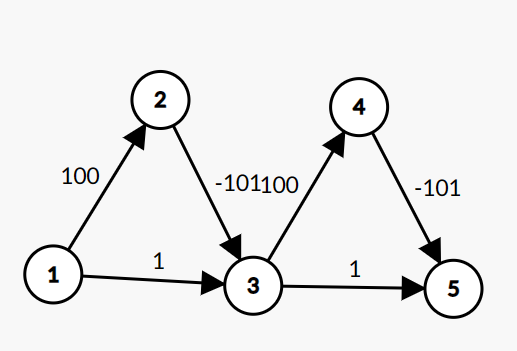
这就是一个小小的例子，我们可以构造这样的结构，骗过 \(Dij\)，让它先走下面的 \(1\)，直到走到了终点，再发现堆里还积压着更优的做法。

如果我们把这样的结构重复 \(k\) 遍，就可以让堆每次释放最后的点。而且我们需要后面的点先出队，也就是较大的这个边权应该是递减的（或者从 \(30\) 到 \(0\)，就可以将其设置为常数而天然由离终点更近的先出堆）。从而把复杂度卡到 \(n^2\)。但是这样显然卡不掉。我们需要的是指数级。

指数级意味着什么呢？意味着我们在第一个结构试错过一次走上对路的时候，依然会把后面所有结构的不优答案再试一遍。那又是什么呢？就是我们每次走对路的优势要从终点到起点递增，大到只要我们当前选的是对的，后面的即使全部选错的，也比当前选错后面全对要小。这样前面轮的答案就不会影响到当前的循环。

也就是，假设我们的每个结构是

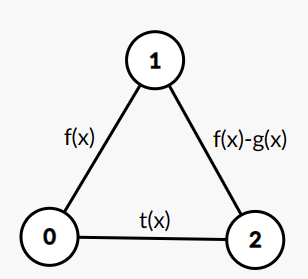
那么 \(f(x)\) 是骗答案不走的大边，\(g(x)\) 是走对路的收益，那么假设从起点到终点的编号依次是 \(n,n-1,n-2,n-3\cdots\)，则 \(g(x)\) 要大于 \(\sum_{i\gl x}g(i)\)。

我们发现，如果我们设 \(g(i)\) 为 \(2^i\)，就满足这一条件。

然后还有什么要求呢？\(f(i)\) 一定要大于所有 \(t(i)\) 的和。我们可以把 \(t(i)\) 设为 \(1\)，\(f(i)\) 设为 \(16\)（\(30\) 作为起点，保证靠近终点的先出堆），\(f(i)-g(i)\) 就可以是 \(16+2^i\)，但是这样麻烦，我们不如设置 \(f(i)-g(i)\) 为 \(2^{i+4}\)，就一定会大于 \(16\) 并且收益满足要求。

这样就可以把 \(Dij\) 卡出指数级。我们重复这个结构 \(16\) 次，一共 \(33\) 个点，\(48\) 条边。每一次询问都可以卡出 \(196606\) 次（所有的结构都是按照 \(2^n\) 重复的，每一个重复结构都会扫所有点，所以实际执行次数是 \((n-1)2^n\)（\(n\) 指结构个数））。循环 \(10\) 次就直接卡掉。

vt<pii>vv[305];
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout<<999<<" "<<1501<<endl;
	for(int i=32;i>=2;i-=2){
		int res=i/2;
		vv[i].pb({i-1,1});
		vv[i].pb({i-2,0});
		vv[i-1].pb({i-2,-(1ll<<(res))});
	}
	rd(i,33){
		cout<<vv[i].size()<<" ";
		for(auto j:vv[i])cout<<j.first<<" "<<j.second<<" ";
		cout<<endl;
	}
	cout<<10<<endl;
	rd(_,10)cout<<32<<" "<<0<<endl;
	return 0;
}
//Crayan_r

5

我们直接把 \(test 2\) 的数据搬过来，但是现在另一个程序换成了 \(Dij\)，那就……放飞自我！我们可以随便卡了，因为都是正权边，\(Dij\) 是 \(100%\) 通过的。不过给的数字个数倒是减小了，但并不会影响我们卡死 \(Bellman-Ford\) 的脚步。我们直接造一个 \(300\)（极限个数）个点的大链，还剩 \(37\) 个边连不连都无所谓了，询问 \(10\) 次，然后 \(Bellman-Ford\) 就直接上西天了。

vt<pii>vv[305];
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout<<300<<endl;
	rep(i,1,299)vv[i].pb({i-1,1});
	int cnt=0;
	rep(i,1,299){
		rep(j,i+1,299){
			vv[j].pb({i,999999});
			cnt++;
			if(cnt==37)break;
		}if(cnt==37)break;
	}
	rd(i,300){
		cout<<vv[i].size()<<" ";
		for(auto j:vv[i])cout<<j.first<<" "<<j.second<<" ";
		cout<<endl;
	}
	cout<<10<<endl;
	rd(_,10)cout<<299<<" "<<0<<endl;
	return 0;
}
//Crayan_r

6

直接套 \(test 4\) 的，三十年河东三十年河西，现在怎么跑都不会挂的轮到我 \(Bellman-Ford\) 啦！！在这么小的点个数，\(Bellman_Ford\) 想挂都不可能。唯一的难点是给的数字数量变少了，我们原来的方案超出了 \(8\) 个数。这怎么办？砍点吗？那就铁定卡不掉了。我们发现跑一次其实可以卡到接近 \(2\cdot 10^5\)，那么跑 \(10\) 次其实是多余的。跑 \(6\) 次就够了。砍掉 \(4\) 次询问，恰好可以通过。

vt<pii>vv[305];
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout<<999<<" "<<1501<<endl;
	for(int i=32;i>=2;i-=2){
		int res=i/2;
		vv[i].pb({i-1,1});
		vv[i].pb({i-2,0});
		vv[i-1].pb({i-2,-(1ll<<(res))});
	}
	rd(i,33){
		cout<<vv[i].size()<<" ";
		for(auto j:vv[i])cout<<j.first<<" "<<j.second<<" ";
		cout<<endl;
	}
	cout<<6<<endl;
	rd(_,6)cout<<32<<" "<<0<<endl;
	return 0;
}
//Crayan_r

7

这个问题只是卡掉这个神秘程序，因为 \(Gamble1\) 是 \(100%\) 通过的。

发现算法强制我们用恰好 \(1501\) 条边。

那么我们考虑这个神秘程序的工作，其实就是通过编号在前面的点的安排方式进行剪枝。那么我们让它剪不掉就好了。具体而言，我们在前若干个点压根不进行任何限制，让他跑，然后后面的点施加很强的限制（造一堆奇环或者造一个比较小的完全图），导致根本没有方案可以用。这样在 \(x=2\) 的时候，算法就会把前面所有的点的所有填涂方式全部枚举一遍，造一个奇环，每一种都到点即停。

然后我们观察一下下发的程序，发现还有点离谱，只有一次搜索结束之后才会出来判断 \(counter\)，虽然不知道死在循环里面能不能过，但是保险起见，把没有任何限制的点设置为前 \(20\) 个点，保证搜满 \(10^6\) 次又保证能退出即可。

vt<pii>vv[1005];
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout<<999<<" "<<1501<<endl;
	int cnt=1501;
	rep(i,21,997){
		cout<<i<<" "<<i+1<<endl;
		cnt--;
	} 
	rep(i,21,996){
		cout<<i<<" "<<i+2<<endl;
		cnt--;
		if(!cnt)break;
	}
	return 0;
}
//Crayan_r

8

我们发现 \(Gamble2\) 是一定会挂的，那么就让这个程序通过就行了。

（让这个程序通过非常简单，随机一个出来就是了）

还是要找靠谱一点的方法的，具体方法就是构造一个二分图，把前 \(500\) 个点和后 \(499\) 个点分开，保证每个点都和另一部分连边。这样自然就能一遍跑出答案。因为前面的是默认的 \(0\)，后面因为每个都和 \(0\) 连边了，第一选择就是 \(1\)。

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout<<999<<" "<<1501<<endl;
	int cnt=1501;
	rep(i,0,448){
		cout<<i<<" "<<i+450<<endl;;cnt--;
	}cnt--;cout<<449<<" "<<450<<endl;
	rep(i,1,449){
		rep(j,450,998)if(j!=i+450){
			cout<<i<<" "<<j<<endl;cnt--;
			if(!cnt)break;
		}
		if(!cnt)break;
	}
	return 0;
}
//Crayan_r

然后就通过了。

另外，洛谷的 \(Bellman-Ford\) 测试程序似乎和下发的程序并不一样，如果在 \(2\) 中只造 \(98\) 的链而非 \(99\)，在 \(5\) 中只造 \(298\) 而非 \(299\)，\(UOJ\) 可以通过，但洛谷卡不满。