FP-growth
一、频繁项集的紧凑表示
1.极大频繁项集
1.极大频繁项集的性质:它的直接超集都不是频繁的,因此,表现为:频繁项集和非频繁项集的分界处
2.作用:极大频繁项集形成了所有频繁项集的最小的项集的集合。
提供了频繁项集的紧凑表示,但是没有提供子集的支持度信息。
2.闭频繁项集
1.提供了频繁项集的最小表示,该表示不丢失支持度信息。
2.闭项集:如果项集是闭的,它的直接超集都不具有和它相同的支持度计数。
反证法定义:如果至少存在一个X的直接超集,其支持度计数与X相同,那么X就不是闭的
3.闭频繁项集
(1)非闭频繁项集的支持度等于它的超集的最大支持度。 => 用闭频繁项集的支持度来计算非闭频繁项集的支持度。
(2)闭频繁项集,可以删除冗余规则。
冗余规则:X->Y,X'->Y',二者具有相同的支持度和置信度,并且,X'是X的子集,Y'是Y的子集,则小的那个,X->Y是冗余的。
例子:
{b}不是闭频繁项集,而{b,c}是闭频繁项集,{b,c}->{d,e}和{b}->{d,e}是具有相同的置信度和支持度,所以{b}->{d,e}是冗余的,所以用闭频繁项集产生规则,不会产生冗余规则。
3.二者联系
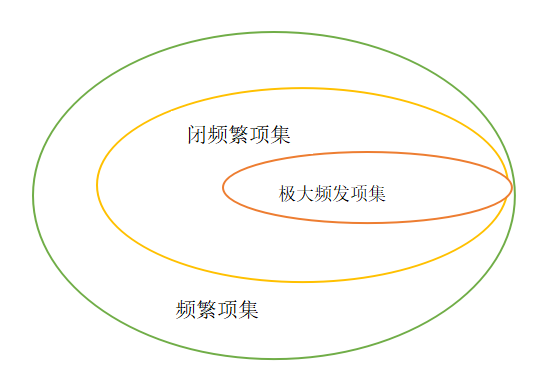
二、产生频繁项集的其他方法
1.从特殊到一般:先寻找更特殊的频繁项集,再发现更一般的频繁项集;对于发现稠密事务中的极大频繁项集是有用的
2.从一般到特殊
3.二者结合
------------恢复内容开始------------
一、频繁项集的紧凑表示
1.极大频繁项集
1.极大频繁项集的性质:它的直接超集都不是频繁的,因此,表现为:频繁项集和非频繁项集的分界处
2.作用:极大频繁项集形成了所有频繁项集的最小的项集的集合。
提供了频繁项集的紧凑表示,但是没有提供子集的支持度信息。
2.闭频繁项集
1.提供了频繁项集的最小表示,该表示不丢失支持度信息。
2.闭项集:如果项集是闭的,它的直接超集都不具有和它相同的支持度计数。
反证法定义:如果至少存在一个X的直接超集,其支持度计数与X相同,那么X就不是闭的
3.闭频繁项集
(1)非闭频繁项集的支持度等于它的超集的最大支持度。 => 用闭频繁项集的支持度来计算非闭频繁项集的支持度。
(2)闭频繁项集,可以删除冗余规则。
冗余规则:X->Y,X'->Y',二者具有相同的支持度和置信度,并且,X'是X的子集,Y'是Y的子集,则小的那个,X->Y是冗余的。
例子:
{b}不是闭频繁项集,而{b,c}是闭频繁项集,{b,c}->{d,e}和{b}->{d,e}是具有相同的置信度和支持度,所以{b}->{d,e}是冗余的,所以用闭频繁项集产生规则,不会产生冗余规则。
3.二者联系
------------恢复内容结束------------





