荷马史诗

题目链接：homo史诗

这道homo(bushi)史诗已经压了好久了，今天终于大概理解了，其实如果是总长度最小的话就是权值*长度，想一个贪心思路，很显然，权值最大的点放在上面很显然更优，而使最大的k进制串

最小显然使它尽量是满叉树就可以了，为了实现这个，只要添加零节点将其顶上去就可以了

那么如何实现呢，我学习到了一个玩应叫做哈夫曼树，这个东西可以实现最小求WPL，只要将权值最小的节点从下开始建树就可以了，下面是蒟蒻的爪子画出来的诡异的图

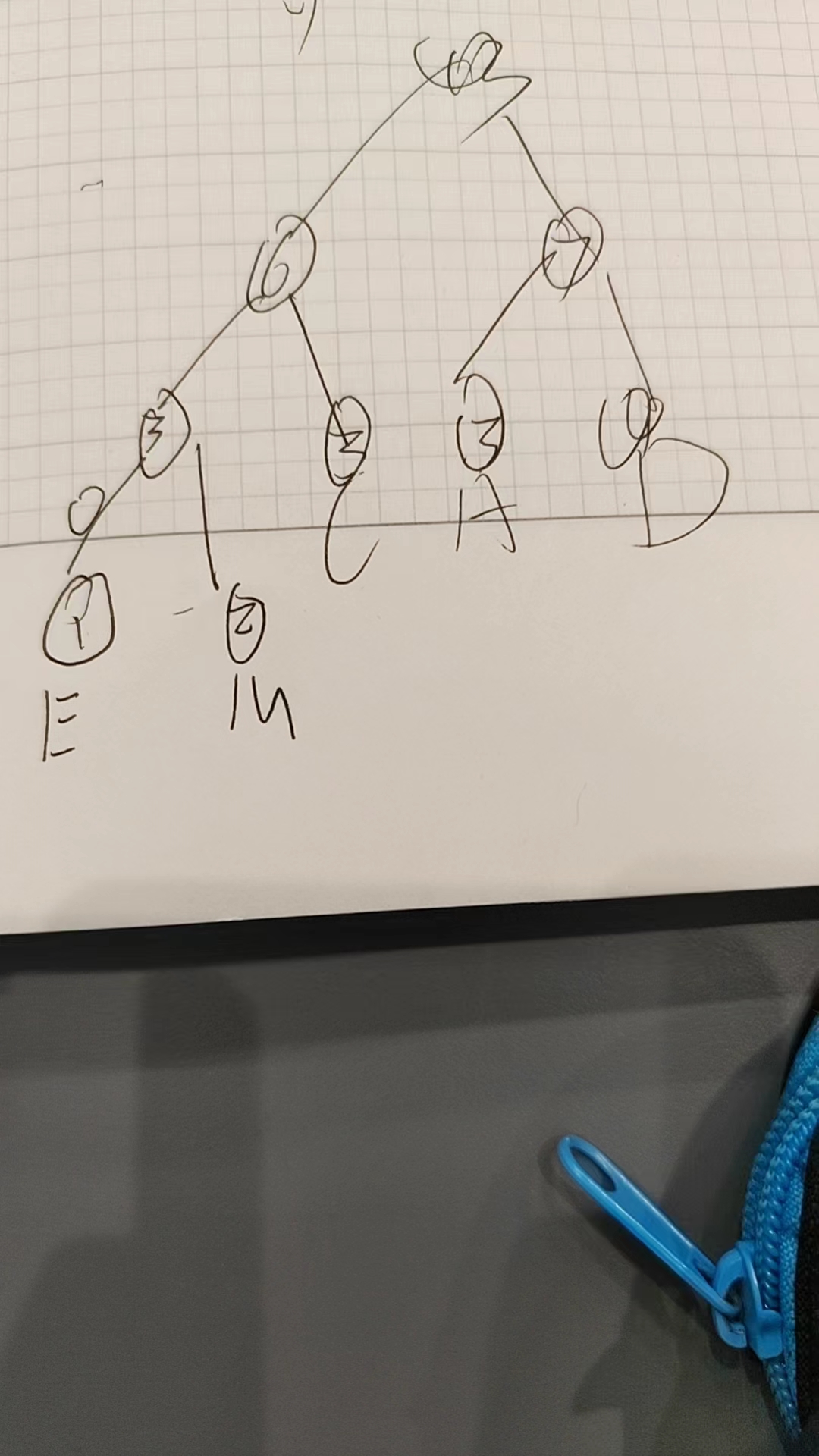
这个描述的情况是有五个节点E,M,C,A,D权值分别为1,2,3,3,4

代码如下

#include<bits/stdc++.h>
//贪心思路，权值较大的点位置偏上使得位数较小 
#define int long long
using namespace std;
struct node {
	int w,h;//w为权值，h表示高度（深度？）
	friend bool operator<(node a,node b){
		if(a.w!=b.w){
			return a.w>b.w;
		}
		else{
			return a.h>b.h;
		}
	} 
};
int ans;
int n,k;
priority_queue<node>q;
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>k;
	for(int i=1;i<=n;i++){
		int w;
		cin>>w;
		q.push(node{w,1});
	}
	while((q.size()-1)%(k-1)){
		q.push(node{0,1});
	}
	while(q.size()>=k){
		int hh=-1;
		int w=0;
		for(int i=1;i<=k;i++){
			node t=q.top();
			q.pop();
			hh=max(hh,t.h);
			w+=t.w;
		}
		ans+=w;
		q.push(node{w,hh+1});
	}
	cout<<ans<<endl<<q.top().h-1<<endl;
	return 0;
}
//文章最短长度应为深度最小
//树的路径长度PL：从树根到树的每个节点的路径长度（每条边长度为1）之和（完全二叉树为这种路径长度最短的二叉树）。
//
//树的带权路径长度WPL：树的所有叶子节点的带权路径长度（该节点到根节点路径长度与节点上权的乘积）之和。 
//结点权值为其出现次数 
//从下向上建树 

`