识别简单的答题卡（Bubble sheet multiple choice scanner and test grader using OMR, Python and OpenCV——jsxyhelu...

该博客转自www.pyimagesearch.com，进行了相关修改补充。

Figure 14: Recognizing bubble sheet exams using computer vision.

Over the past few months I’ve gotten quite the number of requests landing in my inbox to build a bubble sheet/Scantron-like【简而言之答题卡】 test reader using computer vision and image processing techniques.

And while I’ve been having a lot of fun doing this series on machine learning and deep learning, I’d be lying if I said this little mini-project wasn’t a short, welcome break. One of my favorite parts of running the PyImageSearch blog is demonstrating how to build actual solutions to problems using computer vision.【显而易见，pyimageSearch正在向dl方向转型，实际上这也是我准备下一步要做的】

In fact, what makes this project so special is that we are going to combine the techniques from many previous blog posts, including building a document scanner, contour sorting, and perspective transforms. Using the knowledge gained from these previous posts, we’ll be able to make quick work of this bubble sheet scanner and test grader.

You see, last Friday afternoon I quickly Photoshopped an example bubble test paper, printed out a few copies, and then set to work on coding up the actual implementation.

Overall, I am quite pleased with this implementation and I think you’ll absolutely be able to use this bubble sheet grader/OMR system as a starting point for your own projects.【完成一个完整的项目仍然是非常有独特价值的】

Bubble sheet scanner and test grader using OMR, Python, and OpenCV

In the remainder of this blog post, I’ll discuss what exactly Optical Mark Recognition (OMR) is. I’ll then demonstrate how to implement a bubble sheet test scanner and grader using strictly computer vision and image processing techniques, along with the OpenCV library.

Once we have our OMR system implemented, I’ll provide sample results of our test grader on a few example exams, including ones that were filled out with nefarious intent.

Finally, I’ll discuss some of the shortcomings of this current bubble sheet scanner system and how we can improve it in future iterations.

What is Optical Mark Recognition (OMR)?【名称解释】

Optical Mark Recognition, or OMR for short, is the process of automatically analyzing human-marked documents and interpreting their results.【这个定义蛮好】

Arguably, the most famous, easily recognizable form of OMR are bubble sheet multiple choice tests, not unlike the ones you took in elementary school, middle school, or even high school.

If you’re unfamiliar with “bubble sheet tests” or the trademark/corporate name of “Scantron tests”, they are simply multiple-choice tests that you take as a student. Each question on the exam is a multiple choice — and you use a #2 pencil to mark the “bubble” that corresponds to the correct answer.【我在想，这个工作，可以和GOGPY一起，成为一个非常棒的新视频内容】

The most notable bubble sheet test you experienced (at least in the United States) were taking the SATs during high school, prior to filling out college admission applications.

I believe that the SATs use the software provided by Scantron to perform OMR and grade student exams, but I could easily be wrong there. I only make note of this because Scantron is used in over 98% of all US school districts.

In short, what I’m trying to say is that there is a massive market for Optical Mark Recognition and the ability to grade and interpret human-marked forms and exams.

【如果能够结合答题卡的定制，那这个项目将非常完整了。经过一段时间的积累，可以成为拳头项目】这将是10月份的重要工作。

Implementing a bubble sheet scanner and grader using OMR, Python, and OpenCV

Now that we understand the basics of OMR, let’s build a computer vision system using Python and OpenCV that can read and grade bubble sheet tests.

Of course, I’ll be providing lots of visual example images along the way so you can understand exactly what techniques I’m applying and why I’m using them.

Below I have included an example filled in bubble sheet exam that I have put together for this project:

Figure 1: The example, filled in bubble sheet we are going to use when developing our test scanner software.

Figure 1: The example, filled in bubble sheet we are going to use when developing our test scanner software.

We’ll be using this as our example image as we work through the steps of building our test grader. Later in this lesson, you’ll also find additional sample exams.

I have also included a blank exam template as a .PSD (Photoshop) file so you can modify it as you see fit. You can use the “Downloads” section at the bottom of this post to download the code, example images, and template file.【提供模板的doc，我看可以】

The 7 steps to build a bubble sheet scanner and grader

The goal of this blog post is to build a bubble sheet scanner and test grader using Python and OpenCV.

To accomplish this, our implementation will need to satisfy the following 7 steps:【分为7步，这个很专业的写法】

  • Step #1: Detect the exam in an image. 从图像中读取到答题卡
  • Step #2: Apply a perspective transform to extract the top-down, birds-eye-view of the exam. 对图像进行透视变化
  • Step #3: Extract the set of bubbles (i.e., the possible answer choices) from the perspective transformed exam. 从转换结果中获取bubbles
  • Step #4: Sort the questions/bubbles into rows. 按行切割
  • Step #5: Determine the marked (i.e., “bubbled in”) answer for each row. 每行识别
  • Step #6: Lookup the correct answer in our answer key to determine if the user was correct in their choice. 识别
  • Step #7: Repeat for all questions in the exam. 重复

The next section of this tutorial will cover the actual implementation of our algorithm.

The bubble sheet scanner implementation with Python and OpenCV

To get started, open up a new file, name it test_grader.py , and let’s get to work:

On Lines 2-7 we import our required Python packages.

You should already have OpenCV and Numpy installed on your system, but you might not have the most recent version of imutils, my set of convenience functions to make performing basic image processing operations easier. To install imutils  (or upgrade to the latest version), just execute the following command:

Lines 10-12 parse our command line arguments. We only need a single switch here, --image , which is the path to the input bubble sheet test image that we are going to grade for correctness.

Line 17 then defines our ANSWER_KEY .

As the name of the variable suggests, the ANSWER_KEY  provides integer mappings of the question numbers to the index of the correct bubble.

In this case, a key of 0 indicates the first question, while a value of 1 signifies “B” as the correct answer (since “B” is the index 1 in the string “ABCDE”). As a second example, consider a key of 1 that maps to a value of 4 — this would indicate that the answer to the second question is “E”.

As a matter of convenience, I have written the entire answer key in plain english here:

  • Question #1: B
  • Question #2: E
  • Question #3: A
  • Question #4: D
  • Question #5: B

Next, let’s preprocess our input image:

On Line 21 we load our image from disk, followed by converting it to grayscale (Line 22), and blurring it to reduce high frequency noise (Line 23).

We then apply the Canny edge detector on Line 24 to find the edges/outlines of the exam.

Below I have included a screenshot of our exam after applying edge detection:

Figure 2: Applying edge detection to our exam neatly reveals the outlines of the paper.

Figure 2: Applying edge detection to our exam neatly reveals the outlines of the paper.

Notice how the edges of the document are clearly defined, with all four vertices of the exam being present in the image.

Obtaining this silhouette of the document is extremely important in our next step as we will use it as a marker to apply a perspective transform to the exam, obtaining a top-down, birds-eye-view【非常专业的观点】 of the document:

Now that we have the outline of our exam, we apply the cv2.findContours  function to find the lines that correspond to the exam itself.

We do this by sorting our contours by their area (from largest to smallest) on Line 37 (after making sure at least one contour was found on Line 34, of course【边界处理，非常重要】). This implies that larger contours will be placed at the front of the list, while smaller contours will appear farther back in the list.

We make the assumption that our exam will be the main focal point of the image, and thus be larger than other objects in the image. This assumption allows us to “filter” our contours, simply by investigating their area and knowing that the contour that corresponds to the exam should be near the front of the list.

However, contour area and size is not enough — we should also check the number of vertices on the contour.

To do, this, we loop over each of our (sorted) contours on Line 40. For each of them, we approximate the contour, which in essence means we simplify the number of points in the contour, making it a “more basic” geometric shape. You can read more about contour approximation in this post on building a mobile document scanner.

On Line 47 we make a check to see if our approximated contour has four points, and if it does, we assume that we have found the exam.

Below I have included an example image that demonstrates the docCnt  variable being drawn on the original image:

Figure 3: An example of drawing the contour associated with the exam on our original image, indicating that we have successfully found the exam.

Figure 3: An example of drawing the contour associated with the exam on our original image, indicating that we have successfully found the exam.

Sure enough, this area corresponds to the outline of the exam.

Now that we have used contours to find the outline of the exam, we can apply a perspective transform to obtain a top-down, birds-eye-view of the document:

def four_point_transform(image, pts) :
# obtain a consistent order of the points and unpack them
# individually
rect = order_points(pts)
(tl, tr, br, bl) = rect
 
# compute the width of the new image, which will be the
# maximum distance between bottom-right and bottom-left
# x-coordiates or the top-right and top-left x-coordinates
widthA = np.sqrt(((br[ 0] - bl[ 0]) ** 2) + ((br[ 1] - bl[ 1]) ** 2))
widthB = np.sqrt(((tr[ 0] - tl[ 0]) ** 2) + ((tr[ 1] - tl[ 1]) ** 2))
maxWidth = max( int(widthA), int(widthB))
 
# compute the height of the new image, which will be the
# maximum distance between the top-right and bottom-right
# y-coordinates or the top-left and bottom-left y-coordinates
heightA = np.sqrt(((tr[ 0] - br[ 0]) ** 2) + ((tr[ 1] - br[ 1]) ** 2))
heightB = np.sqrt(((tl[ 0] - bl[ 0]) ** 2) + ((tl[ 1] - bl[ 1]) ** 2))
maxHeight = max( int(heightA), int(heightB))
 
# now that we have the dimensions of the new image, construct
# the set of destination points to obtain a "birds eye view",
# (i.e. top-down view) of the image, again specifying points
# in the top-left, top-right, bottom-right, and bottom-left
# order
dst = np. array([
[ 0, 0],
[maxWidth - 1, 0],
[maxWidth - 1, maxHeight - 1],
[ 0, maxHeight - 1]], dtype = "float32")
 
# compute the perspective transform matrix and then apply it
M = cv2.getPerspectiveTransform(rect, dst)
warped = cv2.warpPerspective(image, M, (maxWidth, maxHeight))
 
# return the warped image
return warped

def order_points(pts) :
# initialzie a list of coordinates that will be ordered
# such that the first entry in the list is the top-left,
# the second entry is the top-right, the third is the
# bottom-right, and the fourth is the bottom-left
rect = np.zeros(( 4, 2), dtype = "float32")
 
# the top-left point will have the smallest sum, whereas
# the bottom-right point will have the largest sum
s = pts.sum(axis = 1)
rect[ 0] = pts[np.argmin(s)]
rect[ 2] = pts[np.argmax(s)]
 
# now, compute the difference between the points, the
# top-right point will have the smallest difference,
# whereas the bottom-left will have the largest difference
diff = np.diff(pts, axis = 1)
rect[ 1] = pts[np.argmin(diff)]
rect[ 3] = pts[np.argmax(diff)]
 
# return the ordered coordinates
return rect

 

In this case, we’ll be using my implementation of the four_point_transform  function which:

  1. Orders the (x, y)-coordinates of our contours in a specific, reproducible manner.
  2. Applies a perspective transform to the region.

You can learn more about the perspective transform in this post as well as this updated one on coordinate ordering, but for the time being, simply understand that this function handles taking the “skewed” exam and transforms it, returning a top-down view of the document:

Figure 4: Obtaining a top-down, birds-eye view of both the original image along with the grayscale version.

Figure 4: Obtaining a top-down, birds-eye view of both the original image (left) along with the grayscale version (right).

Alright, so now we’re getting somewhere.

We found our exam in the original image.

We applied a perspective transform to obtain a 90 degree viewing angle of the document.

But how do we go about actually grading the document?

This step starts with binarization, or the process of thresholding/segmenting the foreground from the background of the image:

After applying Otsu’s thresholding method, our exam is now a binary image:

Figure 5: Using Otsu's thresholding allows us to segment the foreground from the background of the image.

现在的关键问题，就是里面有一些重复的项目，如何有效地去除掉。

里面的空洞是否需要去除掉。


。我想，即使是变换成为这样，也是可以的（至少对于这个
项目来说没有问题）

Figure 5: Using Otsu’s thresholding allows us to segment the foreground from the background of the image.

Notice how the background of the image is black, while the foreground is white.

This binarization will allow us to once again apply contour extraction techniques to find each of the bubbles in the exam:

Lines 64-67 handle finding contours on our thresh  binary image, followed by initializing questionCnts , a list of contours that correspond to the questions/bubbles on the exam.

To determine which regions of the image are bubbles, we first loop over each of the individual contours (Line 70).

For each of these contours, we compute the bounding box (Line 73), which also allows us to compute the aspect ratio, or more simply, the ratio of the width to the height (Line 74).

In order for a contour area to be considered a bubble, the region should:

  1. Be sufficiently wide and tall (in this case, at least 20 pixels in both dimensions).
  2. Have an aspect ratio that is approximately equal to 1.

As long as these checks hold, we can update our questionCnts  list and mark the region as a bubble.

Below I have included a screenshot that has drawn the output of questionCnts  on our image:

首先做到这一步，的确是需要的

Figure 6: Using contour filtering allows us to find all the question bubbles in our bubble sheet exam recognition software.

Figure 6: Using contour filtering allows us to find all the question bubbles in our bubble sheet exam recognition software.

Notice how only the question regions of the exam are highlighted and nothing else.

We can now move on to the “grading” portion of our OMR system:

First, we must sort our questionCnts  from top-to-bottom. This will ensure that rows of questions that are closer to the top of the exam will appear first in the sorted list.

We also initialize a bookkeeper variable to keep track of the number of correct  answers.

On Line 90 we start looping over our questions. Since each question has 5 possible answers, we’ll apply NumPy array slicing and contour sorting to to sort the current set of contours from left to right.

The reason this methodology works is because we have already sorted our contours from top-to-bottom. We know that the 5 bubbles for each question will appear sequentially in our list — but we do not know whether these bubbles will be sorted from left-to-right. The sort contour call on Line 94 takes care of this issue and ensures each row of contours are sorted into rows, from left-to-right.

To visualize this concept, I have included a screenshot below that depicts each row of questions as a separate color:

Figure 7: By sorting our contours from top-to-bottom, followed by left-to-right, we can extract each row of bubbles. Therefore, each row is equal to the bubbles for one question.
他思路挺好的

Figure 7: By sorting our contours from top-to-bottom, followed by left-to-right, we can extract each row of bubbles. Therefore, each row is equal to the bubbles for one question.

Given a row of bubbles, the next step is to determine which bubble is filled in.

We can accomplish this by using our thresh  image and counting the number of non-zero pixels (i.e., foreground pixels) in each bubble region:

Line 98 handles looping over each of the sorted bubbles in the row.

We then construct a mask for the current bubble on Line 101 and then count the number of non-zero pixels in the masked region (Lines 107 and 108). The more non-zero pixels we count, then the more foreground pixels there are, and therefore the bubble with the maximum non-zero count is the index of the bubble that the the test taker has bubbled in (Line 113 and 114).

Below I have included an example of creating and applying a mask to each bubble associated with a question:

Figure 8: An example of constructing a mask for each bubble in a row.

Figure 8: An example of constructing a mask for each bubble in a row.

Clearly, the bubble associated with “B” has the most thresholded pixels, and is therefore the bubble that the user has marked on their exam.

This next code block handles looking up the correct answer in the ANSWER_KEY , updating any relevant bookkeeper variables, and finally drawing the marked bubble on our image:

Based on whether the test taker was correct or incorrect yields which color is drawn on the exam. If the test taker is correct, we’ll highlight their answer in green. However, if the test taker made a mistake and marked an incorrect answer, we’ll let them know by highlighting the correct answer in red:

Figure 9: Drawing a "green" circle to mark "correct" or a "red" circle to mark "incorrect".

Figure 9: Drawing a “green” circle to mark “correct” or a “red” circle to mark “incorrect”.

Finally, our last code block handles scoring the exam and displaying the results to our screen:

Below you can see the output of our fully graded example image:

Figure 10: Finishing our OMR system for grading human-taken exams.

Figure 10: Finishing our OMR system for grading human-taken exams.

In this case, the reader obtained an 80% on the exam. The only question they missed was #4 where they incorrectly marked “C” as the correct answer (“D” was the correct choice).

Why not use circle detection?【这个也可以提及一下】

After going through this tutorial, you might be wondering:

“Hey Adrian, an answer bubble is a circle. So why did you extract contours instead of applying Hough circles to find the circles in the image?”

Great question.

To start, tuning the parameters to Hough circles on an image-to-image basis can be a real pain. But that’s only a minor reason.

The real reason is:

User error.

How many times, whether purposely or not, have you filled in outside the lines on your bubble sheet? I’m not expert, but I’d have to guess that at least 1 in every 20 marks a test taker fills in is “slightly” outside the lines.

And guess what?

Hough circles don’t handle deformations in their outlines very well — your circle detection would totally fail in that case.

Because of this, I instead recommend using contours and contour properties to help you filter the bubbles and answers. The cv2.findContours  function doesn’t care if the bubble is “round”, “perfectly round”, or “oh my god, what the hell is that?”.

Instead, the cv2.findContours  function will return a set of blobs to you, which will be the foreground regions in your image. You can then take these regions process and filter them to find your questions (as we did in this tutorial), and go about your way.

Our bubble sheet test scanner and grader results

To see our bubble sheet test grader in action, be sure to download the source code and example images to this post using the “Downloads” section at the bottom of the tutorial.

We’ve already seen test_01.png  as our example earlier in this post, so let’s try test_02.png :

Here we can see that a particularly nefarious user took our exam. They were not happy with the test, writing “#yourtestsux” across the front of it along with an anarchy inspiring “#breakthesystem”. They also marked “A” for all answers.

Perhaps it comes as no surprise that the user scored a pitiful 20% on the exam, based entirely on luck:

Figure 11: By using contour filtering, we are able to ignore the regions of the exam that would have otherwise compromised its integrity.

Figure 11: By using contour filtering, we are able to ignore the regions of the exam that would have otherwise compromised its integrity.

Let’s try another image:

This time the reader did a little better, scoring a 60%:

Figure 12: Building a bubble sheet scanner and test grader using Python and OpenCV.

Figure 12: Building a bubble sheet scanner and test grader using Python and OpenCV.

In this particular example, the reader simply marked all answers along a diagonal:

Figure 13: Optical Mark Recognition for test scoring using Python and OpenCV.

Figure 13: Optical Mark Recognition for test scoring using Python and OpenCV.

Unfortunately for the test taker, this strategy didn’t pay off very well.

Let’s look at one final example:

Figure 14: Recognizing bubble sheet exams using computer vision.

Figure 14: Recognizing bubble sheet exams using computer vision.

This student clearly studied ahead of time, earning a perfect 100% on the exam.

Extending the OMR and test scanner【判重判漏应该首先来做，这也是启示】

Admittedly, this past summer/early autumn has been one of the busiest periods of my life, so I needed to timebox the development of the OMR and test scanner software into a single, shortened afternoon last Friday.

While I was able to get the barebones of a working bubble sheet test scanner implemented, there are certainly a few areas that need improvement. The most obvious area for improvement is the logic to handle non-filled in bubbles.

In the current implementation, we (naively) assume that a reader has filled in one and only one bubble per question row.

However, since we determine if a particular bubble is “filled in” simply by counting the number of thresholded pixels in a row and then sorting in descending order, this can lead to two problems:

  1. What happens if a user does not bubble in an answer for a particular question?
  2. What if the user is nefarious and marks multiple bubbles as “correct” in the same row?

Luckily, detecting and handling of these issues isn’t terribly challenging, we just need to insert a bit of logic.

For issue #1, if a reader chooses not to bubble in an answer for a particular row, then we can place a minimum threshold on Line 108 where we compute cv2.countNonZero :

Figure 15: Detecting if a user has marked zero bubbles on the exam.

Figure 15: Detecting if a user has marked zero bubbles on the exam.

If this value is sufficiently large, then we can mark the bubble as “filled in”. Conversely, if total  is too small, then we can skip that particular bubble. If at the end of the row there are no bubbles with sufficiently large threshold counts, we can mark the question as “skipped” by the test taker.

A similar set of steps can be applied to issue #2, where a user marks multiple bubbles as correct for a single question:

Figure 16: Detecting if a user has marked multiple bubbles for a given question.

Figure 16: Detecting if a user has marked multiple bubbles for a given question.

Again, all we need to do is apply our thresholding and count step, this time keeping track if there are multiple bubbles that have a total  that exceeds some pre-defined value. If so, we can invalidate the question and mark the question as incorrect.

Summary

In this blog post, I demonstrated how to build a bubble sheet scanner and test grader using computer vision and image processing techniques.

Specifically, we implemented Optical Mark Recognition (OMR) methods that facilitated our ability of capturing human-marked documents and automatically analyzing the results.

Finally, I provided a Python and OpenCV implementation that you can use for building your own bubble sheet test grading systems.

If you have any questions, please feel free to leave a comment in the comments section!

But before you, be sure to enter your email address in the form below to be notified when future tutorials are published on the PyImageSearch blog!
应该说，在最后段处理的地方，我采用了更好的思路：

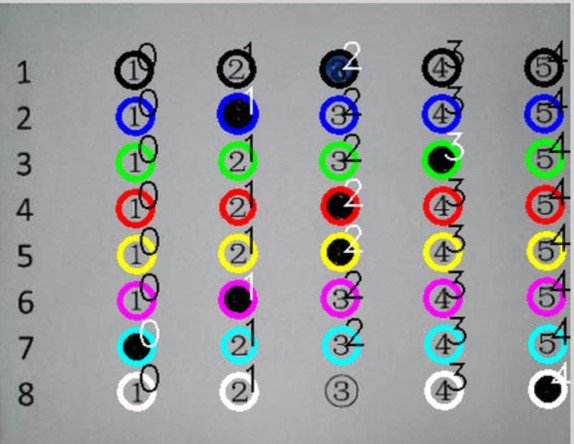下一步，建立更进一步的数据结构，稳固算法，的确实还有很多一些需要思考的地方。这个在课程制作的过程中进一步地研究实现。
#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
#include <iostream>
using namespace cv;
using namespace std;
//4舍5入
int round_double(double number)
{
    return (number > 0.0) ? (number + 0.5) : (number - 0.5); 
}
int main( void )
{
    vector<Scalar> color;
    color.push_back(Scalar(0,0,0));
    color.push_back(Scalar(255,0,0));
    color.push_back(Scalar(0,255,0));
    color.push_back(Scalar(0,0,255));
    color.push_back(Scalar(0,255,255));
    color.push_back(Scalar(255,0,255));
    color.push_back(Scalar(255,255,0));
    color.push_back(Scalar(255,255,255));
    Mat src = imread("e:/template/bubbles.jpg");
    Mat gray;
    cvtColor(src,gray,COLOR_BGR2GRAY);
    Mat tmp;
    threshold(gray,tmp,0,255,THRESH_BINARY_INV |THRESH_OTSU);
    //形态学变化，确保联线
    Mat element = getStructuringElement(MORPH_RECT,Size(3,3));
    morphologyEx(tmp,tmp,CV_MOP_CLOSE,element);
    //寻找轮廓
    vector<vector<Point> > contours;
    findContours( tmp, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
    //筛选轮廓
    vector<Rect> boundRect( contours.size() );
    vector<vector<Point> > questionCnts;
    vector<Rect> questionRects;
    for( int i = 0; i < contours.size(); i++ )
    { 
        boundRect[i] = boundingRect( Mat(contours[i]) );
        if (boundRect[i].width>20 && boundRect[i].height>20 )
        {
            questionCnts.push_back(contours[i]);
            questionRects.push_back(boundRect[i]);
        }
    }
    
    // TODO：if questionCnts.size != 40 then
    //寻找并绘制轮廓外接圆
    vector<vector<Point> > contours_poly( questionCnts.size() );
    vector<Point2f>center( questionCnts.size() );
    vector<float>radius( questionCnts.size() );
    for( int i = 0; i < questionCnts.size(); i++ )
    {
        approxPolyDP( Mat(questionCnts[i]), contours_poly[i], 3, true );
        minEnclosingCircle( contours_poly[i], center[i], radius[i] );
        circle(src,center[i],radius[i],Scalar(0,0,255),1);
    }
    //行运算
    float fmax = 0;
    int maxContourIdx = 0;
    float fmin = 9999;
    int minContourIdx = 0;
    for (int i =0 ;i<center.size();i++)
    {
        if (center[i].y > fmax)
        {
            maxContourIdx= i;
            fmax = center[i].y;
            
        }
        if (center[i].y < fmin)
        {
            minContourIdx = i;
            fmin = center[i].y;
            
        }
    }
    
    float fgap = (fmax - fmin)/7;
    for (int i =0 ;i<center.size();i++)
    {
        int iline =round_double((center[i].y - fmin)/fgap);
        circle(src,center[i],radius[i],color[iline],3);
    }
    //非零点计算
    float NonZeroMax = 0;
    float NonZeroMin = 9999;
    for (int i =0 ;i<questionCnts.size();i++)
    {
        Mat data = tmp(questionRects[i]);
        if (countNonZero(data) > NonZeroMax)
        {
            NonZeroMax = countNonZero(data);
        }
        if(countNonZero(data) < NonZeroMin)
        {
            NonZeroMin =  countNonZero(data);
        }
    }
    //列运算
    fmax = 0;
    maxContourIdx = 0;
    fmin = 9999;
    minContourIdx = 0;
    for (int i =0 ;i<center.size();i++)
    {
        if (center[i].x > fmax)
        {
            maxContourIdx= i;
            fmax = center[i].x;
        }
        if (center[i].x < fmin)
        {
            minContourIdx = i;
            fmin = center[i].x;
        }
    }
    //打印最终结果
    fgap = (fmax - fmin)/4;
    for (int i =0 ;i<center.size();i++)
    {
        int iline =round_double((center[i].x - fmin)/fgap);
        char cbuf[255];
        sprintf_s(cbuf,"%d",iline);
        float NonZero = countNonZero(tmp(questionRects[i]));
        if ( abs(NonZero-NonZeroMax) <  abs(NonZero-NonZeroMin)) //做一个距离运算
        { 
            putText(src,cbuf,center[i],CV_FONT_HERSHEY_DUPLEX,1.0f,Scalar(255,255,255));
        }
        else
        {
            putText(src,cbuf,center[i],CV_FONT_HERSHEY_DUPLEX,1.0f,Scalar(0,0,0));
        }
       
    }
    waitKey();
    return 0;
}





附件列表

     

    posted on 2022-12-03 15:30  jsxyhelu  阅读(63)  评论(0)  编辑  收藏  举报

    导航