第一章 使用神经网络识别手写数字-2 Sigmoid神经元
原文:http://neuralnetworksanddeeplearning.com/chap1.html#sigmoid_neurons
学习算法听起来牛逼哄哄。但我们如何为神经网络设计一个这样子的算法呢?假设我们有一个感知器网络,我们打算用它来学习解决一些问题。比如,网络的输入可能是来自扫描手写数字图像的原始数据,我们期望该网络通过学习权重和偏差使得它的输出正确地将数字分类。为了看看学习是怎么运作的,假设我们稍稍改变一下网络中一些权重(或者偏差)参数的大小,变化要小是为了相应地只对网络的输出带来一点点的改变,稍后我们能够以看到,这个特性让学习成为了可能,如下图,这就是我们想要的(显然这个网络还太简单,不足以实现手写识别):
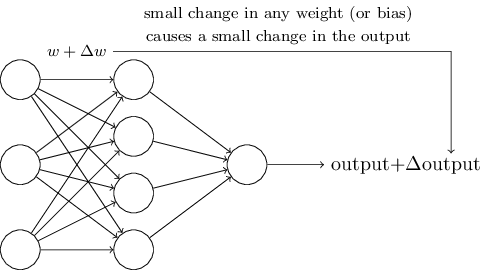
如果一点点权重或者偏差的改变也只使得输出作出很小的变化,那我们能够根据这个事实来改变权重和偏差使得我们的网络越来越接近我们的意图。举个例子,假如网络错误地将一张‘9’的图片分辨成‘8’,我们可以找出改变一点权重和偏差使得网络更接近于把图片分辨成‘9’的办法,然后我们重复操作,一点一点地改变权重和偏差直到输出越来越理想,该网络便能学习。
问题是,这在我们的感知器网络中并不会发生。事实上,网络中任何一个感知器权重或偏差发生一点小小的变化,都可能导致输出完全翻转,从0变成1,这一翻转可能造成网络中其余的行为以某种复杂的途径发生翻天覆地的变化,所以可能现在‘9’是正确识别出来了,所有其它图片上,神经网络的行为却可能难以控制地全都变了。很难看的出要如何一点点地改变权重和偏差来让网络更接近我们想要的行为。也许有许多聪明的方法来解决这个问题,但是如何使得一个感知器网络能够学习还不是很有头绪。
为了克服这个问题我们可以采用一种新型人工神经元——sigmoid神经元。Sigmoid神经元和感知器很像,但是经过了修改使得它们权重和偏差的小变化只会引起输出发生一点小变化,这是sigmoid神经网络能够学习的关键。
好了,让我来描述一下sigmoid神经元,我们以描绘感知器相同的方式来描述sigmoid神经元:

和感知器一样,sigmoid神经元有许多输入,x1,x2……但除了能够输入0和1,它们还能输入0到1之间的任何数,比如0.638……是sigmoid神经元的一个合法输入。而且和感知器一样,sigmoid神经元每个输入也有一个权重参数,w1,w2……和一个偏差bias,b,但是sigmoid神经元的输出不是0或者1,而是σ(w·x + b),σ叫做sigmoid函数,定义如下:(σ[sigma]有时候称为the logistic function)
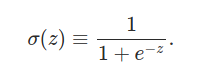
更进一步明确这个定义,以x1,x2……为输入,w1,w2……为权重,b为偏差的sigmoid神经元的输出如下:
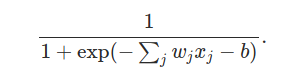
乍一看,sigmoid神经元和感知器差别很大,如果你对这个sigmoid方程的代数式了解不多,它看起来真是晦涩难懂。事实上,感知器和sigmoid神经元是有许多相似之处的,而且事实证明,与其说这个方程式是理解的障碍,不如说是更多的技术细节(开车的人并不一定需要懂得造车的细节)
要理解其与感知器模型的相似之处,我们假设z≡w•x + b是一个很大很大的正数,于是e-z≈0,所以σ(z)≈1。还句话说,当z=w•x + b远大与0,sigmoid神经元的输出约等于1,就像一个感知器一样,另一方面,假设z=w•x + b是个很小的负数,则e-z →∞,σ(z)≈0,所以当z=w•x + b是一个“很负的”负数时,sigmoid神经元的行为也很接近感知器,只有当z=w•x + b处在一段合适的区间中,才和感知器有比较大的区别。
σ的代数式有什么含义?我们能否理解它?事实上σ的确切形式一点儿也不重要,真正重要的是这个方程绘制出来的样子(注意横坐标和纵坐标的比例不一样,这里只是为了显得好看一些):
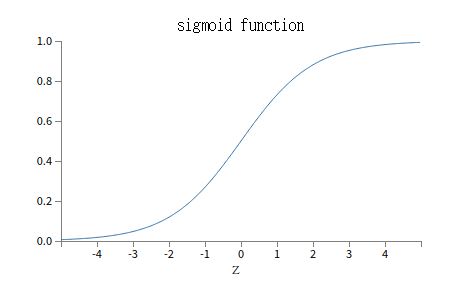
这个形状是阶跃函数[step function]的平滑版本:
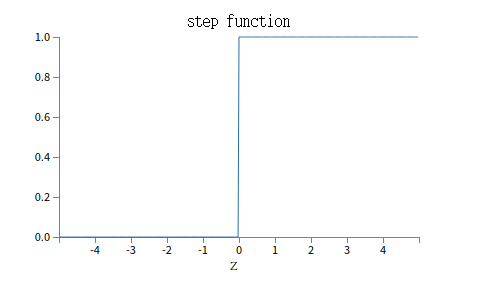
如果σ是一个阶跃函数,那么sigmoid神经元便退化成一个感知器,即基于w•x + b是正数还是负数,它的输出为1或者0(w•x + b=0时输出为0,严格来讲和step function不一样,明白就好),实际上我们常常使用的σ,是上面的那个平滑版本(随着发展现在有更好的),确实,σ函数的关键因子是其平滑性,而不是式子细节。σ的平滑性意味着权重的小变化Δwj、偏差小变化Δb会产生一个小的输出Δoutput。微积分告诉我们Δoutput逼近于(所有变化量的总和):
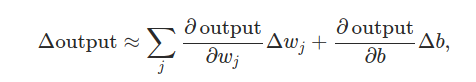
δoutput/δwj是输出output对wj的偏导,δoutput/δb是output对b的偏导,如果你看到偏导就头大也别慌,尽管上面那个表达式包含着偏导数看起来很复杂,实际上它表达的东西很简单(这是一个好消息):Δoutput是权重Δwj、偏差Δb变化的线性函数,这种线性关系使得选择合适的权重和偏差小变动以达到输出的理想小变动变得容易,所以尽管sigmoid神经元和感知器在性质上有许多相同点,我们更容易理清楚怎样改变权重和偏差会改变输出(更加可控)。
如果σ的形状才真的重要,而不是它的确切表达式,那么为什么σ偏偏是这样子【σ(z)=1/(1+e-z)】的呢?事实上,稍后书里会偶尔讨论到一些神经元输出的其它激活函数(f(w•x+b)中的f)。当我们使用一个不同的激活函数,最主要的不同就是下式中偏导数的特殊值发生了变化
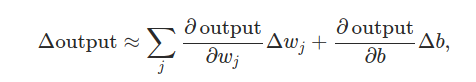
后面我们算到那些特殊的偏导数再引出。使用σ将简化代数,因为幂指数在微分的时候有着讨喜的性质,好歹,σ在神经网络的工作中常常使用,而且它是本书中我们用的最多的激活函数了。
我们应该如何阐释sigmoid神经元的输出呢?显然地,感知器和sigmoid神经元的一个重大不同点就是sigmoid神经元不止输出0和1,它们能够输出0到1之间的任意实数,如0.173……0.689……都是合法的输出。这很有用处,举个例子,如果我们想要使用输出值来代表一张输入神经网络的图像中像素的平均强度。但有时这又变成一个累赘,假如我们想要这个输出表示“输入图像是一个9”,或者“输入图像不是一个9”,显然,最简单的方法就是判断输出是一个0还是一个1,像感知器那样。但是在练习中我们能够制定一个规定来处理这个问题。比如,任何输出大于等于0.5我们便认为它表示这“是一个9”,小于0.5的输出表示“不是9”,我将会始终明确什么情况下我们会使用这样一个规定,这样就不会造成任何混乱。
练习:
- Sigmoid神经元模拟感知器,第一部分
假设我们取得一个感知器网络的所有权重和偏差参数,然后将它们乘以一个正数常量,c>0。证明该网络的行为不会改变。
output = 0 if c(wx + b) <= 0;
output = 1 if c(wx +b) > 0
当c>0时,if后面的式子符号不会改变,依然成立,与原来的感知器输出一样
- Sigmoid神经元模拟感知器,第二部分
假设我们有和上个问题一样的设定,一个感知器网络。再假设网络的所有输入都设定好了,我们不需要确切的输入值,只需要输入是固定不变的,所有的权重和偏差,对任意特定的感知器的输入x,都满足w•x + b ≠ 0,现在把所有的感知器都替换成sigmoid神经元,所有的权重和偏差都乘以一个正数c>0。证明当c→∞,sigmoid神经网络的行为和感知器网络完全一致,当其中有一个感知器w•x + b = 0时,怎么就不成立了?
σ(z) = 1 / (1+e-z ) = 1 / (1+e-Σc(wx+b) ),
wx+b > 0时, c(wx+b) → +∞, e-Σc(wx+b) → 0 => σ(z) = 1
wx+b < 0时, c(wx+b) → -∞, e-Σc(wx+b) → +∞ => σ(z) = 0
因此和感知器行为完全一致,当wx+b=0时,c(wx+b)=0, σ(z) = 1 / (1+e0) = 1/2 = 0.5,这和感知器就不一样了。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号