B-树和B+树和B*树和R树
在大规模数据存储中,实现索引查询这样一个实际背景下,树节点存储的元素数量是有限的(如果元素数量非常多的话,查找就退化成节点内部的线性查找了),这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下,那么如何减少树的深度(当然是不能减少查询的数据量),一个基本的想法就是:采用多叉树结构(由于树节点元素数量是有限的,自然该节点的子树数量也就是有限的)。
为了更有效的减少树的深度,新的查找树结构——多路查找树。根据平衡二叉树的启发,自然就想到平衡多路查找树结构。即B树结构。
磁盘读取数据是以盘块(block)为基本单位的。位于同一盘块中的所有数据都能被一次性全部读取出来。而磁盘IO代价主要花费在查找时间Ts上。因此我们应该尽量将相关信息存放在同一盘块,同一磁道中。或者至少放在同一柱面或相邻柱面上,以求在读/写信息时尽量减少磁头来回移动的次数,避免过多的查找时间Ts。
所以,在大规模数据存储方面,大量数据存储在外存磁盘中,而在外存磁盘中读取/写入块(block)中某数据时,首先需要定位到磁盘中的某块。
1.B-树(B树)
1)定义
B是balanced,而不是binary,B-树或B_树不要误解成“B减树”,“-”“_”只是连字符。
是一种多路搜索树(并不是二叉的),一个M阶的B树:
1.根结点的儿子数为[2, M];
2.除根结点以外的非叶子结点的儿子数为[M/2, M];
3.所有叶子结点位于同一层;
如:(M=3)

2)操作
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点。
由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占M/2的结点;
当插入后节点不满足儿子数为[M/2, M]时,要把这个结点分裂为两个,并把中间的一个关键字(中间的关键字满足:左边的小于该关键字;右边的大于该关键字;故正好可以作为双亲)拿出来插到该结点的双亲结点中去,双亲结点也可能是满的,就需要再分裂、再往上插,从而可能导致B-树可能朝着根的方向生长。
删除结点时,需将两个不足M/2的兄弟结点合并;
当删除后节点不满足儿子数为[M/2, M]时,需要把删除了的结点、它的兄弟结点及它们双亲结点中的一个关键字合并为一个结点。
2.B+树
B+树是B-树的变体,也是一种多路搜索树:
1.有n棵子树的结点中含有n个关键字; (而B 树是n棵子树有n-1个关键字)
2.所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。 (而B 树的非终节点也包含需要查找的有效信息)
如:(M=3)

B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找。
B+树的插入与B树的插入过程类似。不同的是B+树在叶结点上进行,如果叶结点中的关键码个数超过m,就必须分裂成关键码数目大致相同的两个结点,并保证上层结点中有这两个结点的最大关键码。
B+树的删除也仅在叶子结点进行,当叶子结点中的最大关键字被删除时,其在非终端结点中的值可以作为一个“分界关键字”存在。若因删除而使结点中关键字的个数少于m/2 (m/2结果取上界,如5/2结果为3)时,其和兄弟结点的合并过程亦和B-树类似。
优点:
1) B+树的磁盘读写代价更低
B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
2) B+树的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
3.B*树
B*Tree是B+树的变体,在B+Tree的叶节点再增加指向兄弟的指针。
叶节点实际上构成了一个双向链表,一旦发现要从叶节点中的哪里开始,执行值的有序扫描就会很容易。就不用再在整个树结构中导航,而只需根据需要通过叶节点向前或向后扫描就可以了。所以非常适合区间搜索。
4.R树
R树很好的解决了这种高维空间搜索问题。它把B树的思想很好的扩展到了多维空间,采用了B树分割空间的思想,并在添加、删除操作时采用合并、分解结点的方法,保证树的平衡性。因此,R树就是一棵用来存储高维数据的平衡树。
eg:地图上根据经纬度坐标查找,需要x,y共同起作用来搜索。
每个R树的叶子结点包含了多个指向不同数据的指针。
R树采用了一种称为MBR(Minimal Bounding Rectangle)的方法,在此我把它译作“最小边界矩形”。从叶子结点开始用矩形(rectangle)将空间框起来,结点越往上,框住的空间就越大,以此对空间进行分割。
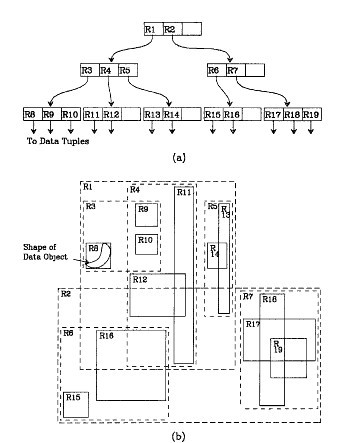
参考:百度百科
http://hi.baidu.com/leibin_neu/item/74c018b9b09ebad885dd7945
http://www.cnblogs.com/biyeymyhjob/archive/2012/07/25/2608880.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号