最短路径
1.Dijskra最短路径算法
1)所需数据结构
节点结构：邻居列表adjacency list、是否已访问过known、起点到此节点的长度distance、路径上一个节点。
优先队列：保存节点长度，以此选出最小的节点长度的节点来进行访问。
2)松弛技术RELAX的介绍
Dijkstra 算法使用了松弛技术，对每个顶点v<-V，都设置一个属性d[v]，用来描述从源点s到v的最短路径上权值的上界，称为最短路径的估计。
3)此Dijkstra 算法分三个步骤， (广度优先遍历)
INSERT (第3行), EXTRACT-MIN (第5行), 和DECREASE-KEY(第8行的RELAX，调用此减小关键字的操作)。
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s) //对每个顶点初始化 ，O(V)
2 S ← Ø
3 Q ← V[G] //INSERT，O(1)
4 while Q ≠ Ø
5 do u ← EXTRACT-MIN(Q) //简单的O(V*V)；二叉/项堆，和FIB-HEAP的话，则都为O(V*lgV)。
6 S ← S ∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w) //简单方式:O(E)，二叉/项堆，E*O(lgV)，FIB-HEAP，E*O(1)。
RELAX(u, v, w)
1 if d[v] > d[u] + w(u, v)
2 then d[v] ← d[u] + w(u, v)
3 π[v] ← u //O（E）
2.A*算法
1)需要数据结构
创建两个表，OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。
节点的 g(n)和 h(n) 和 父节点
2)选取路径的方式
3) eg:假设有人想从A点移动到一墙之隔的B点，如下图，绿色的是起点A，红色是终点B，蓝色方块是中间的墙。
目标路径：
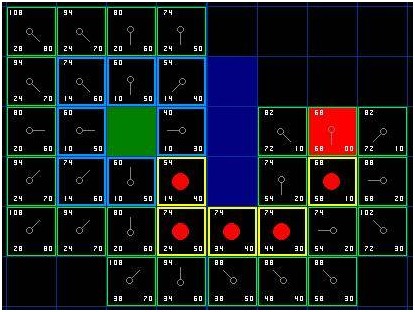
h(n)可以用不同的方法估算。我们这里使用的方法被称为曼哈顿方法，它计算从当前格到目的格之间水平和垂直的方格的数量总和，忽略对角线方向，然后把结果乘以10。这被称为曼哈顿方法是因为它看起来像计算城市中从一个地方到另外一个地方的街区数，在那里你不能沿对角线方向穿过街区。很重要的一点，我们忽略了一切障碍物。这是对剩余距离的一个估算，而非实际值，这也是这一方法被称为启发式的原因。
流程
1，把起始格添加到开启列表。(并执行第二步的c)
2，重复如下的工作：
a) 寻找开启列表中f(n)值最低的格子。我们称它为当前格。
b) 把它切换到关闭列表。
c) 对相邻的格中的每一个
* 如果它不可通过或者已经在关闭列表中，略过它。反之如下。
* 如果它不在开启列表中，把它添加进去。把当前格作为这一格的父节点。记录这一格的father,g(n),和h(n)值。
* 如果它已经在开启列表中，用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。如果是这样，就把这一格的父节点改成当前格，并且重新计算这一格的G和F值。如果你保持你的开启列表按f(n)值排序，改变之后你可能需要重新对开启列表排序。
d) 停止，当你
* 把目标格添加进了关闭列表，这时候路径被找到，或者
* 没有找到目标格，开启列表已经空了。这时候，路径不存在。
3.保存路径。从目标格开始，沿着每一格的父节点移动直到回到起始格。这就是你的路径。
